生成瓦茨-斯特罗加茨小世界图形模型
此示例演示如何构建并分析瓦茨-斯特罗加茨小世界图形。瓦茨-斯特罗加茨模型是一个包含小世界网络属性(例如集群和平均短路径长度)的随机图形。
算法说明
创建瓦茨-斯特罗加茨图形包含以下两个基本步骤:
创建一个环形网格,其中包含
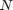 个平均出入度为
个平均出入度为 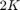 的节点。每个节点都与任一侧的
的节点。每个节点都与任一侧的 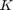 个最近邻点相连。
个最近邻点相连。对于图中的每条边,重新连接概率为
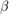 的目标节点。重新连接的边不能是重复或自环的。
的目标节点。重新连接的边不能是重复或自环的。
执行第一步操作之后,图形将是一个完美的环形网格。因此当  时,不会重新连接任何边,并且该模型会返回一个环形网格。而如果
时,不会重新连接任何边,并且该模型会返回一个环形网格。而如果 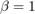 ,则所有边都将重新连接,并且环形网格会变成随机图形。
,则所有边都将重新连接,并且环形网格会变成随机图形。
文件 WattsStrogatz.m 对无向图实现该图算法。根据上面的算法说明,输入参数为 N、K 和 beta。
查看文件 WattsStrogatz.m。
% Copyright 2015 The MathWorks, Inc. function h = WattsStrogatz(N,K,beta) % H = WattsStrogatz(N,K,beta) returns a Watts-Strogatz model graph with N % nodes, N*K edges, mean node degree 2*K, and rewiring probability beta. % % beta = 0 is a ring lattice, and beta = 1 is a random graph. % Connect each node to its K next and previous neighbors. This constructs % indices for a ring lattice. s = repelem((1:N)',1,K); t = s + repmat(1:K,N,1); t = mod(t-1,N)+1; % Rewire the target node of each edge with probability beta for source=1:N switchEdge = rand(K, 1) < beta; newTargets = rand(N, 1); newTargets(source) = 0; newTargets(s(t==source)) = 0; newTargets(t(source, ~switchEdge)) = 0; [~, ind] = sort(newTargets, 'descend'); t(source, switchEdge) = ind(1:nnz(switchEdge)); end h = graph(s,t); end
环形网格
使用 WattsStrogatz 函数构建包含 500 个节点的环形网格。beta 为 0 时,该函数会返回其节点出入度均为 2K 的环形网格。
h = WattsStrogatz(500,25,0); plot(h,'NodeColor','k','Layout','circle'); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0$', ... 'Interpreter','latex')

一些随机边
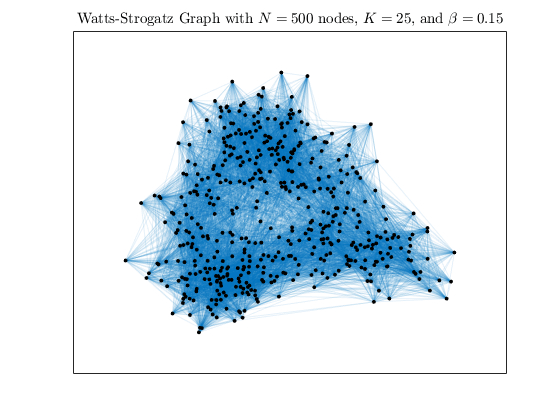
通过将 beta 增大到 0.15 和 0.50,增加图形中的随机性。
h2 = WattsStrogatz(500,25,0.15); plot(h2,'NodeColor','k','EdgeAlpha',0.1); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0.15$', ... 'Interpreter','latex')
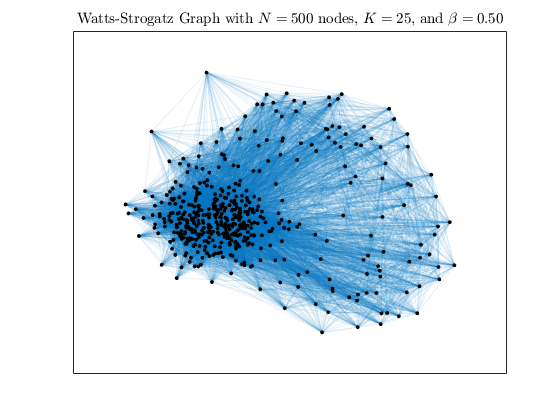
h3 = WattsStrogatz(500,25,0.50); plot(h3,'NodeColor','k','EdgeAlpha',0.1); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0.50$', ... 'Interpreter','latex')
随机图形
通过将 beta 增大到其最大值 1.0,生成一个完全随机的图形。这会重新连接所有边。
h4 = WattsStrogatz(500,25,1); plot(h4,'NodeColor','k','EdgeAlpha',0.1); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 1$', ... 'Interpreter','latex')
出入度分布
不同瓦茨-斯特罗加茨图形中节点的出入度分布会有所不同。beta 为 0 时,这些节点的出入度均为 2K,因此出入度分布只是一个以 2K 为中心的 Dirac-delta 函数 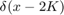 。但是,随着
。但是,随着 beta 的增大,出入度分布也会发生变化。
该绘图显示 beta 的非零值的出入度分布。
histogram(degree(h2),'BinMethod','integers','FaceAlpha',0.9); hold on histogram(degree(h3),'BinMethod','integers','FaceAlpha',0.9); histogram(degree(h4),'BinMethod','integers','FaceAlpha',0.8); hold off title('Node degree distributions for Watts-Strogatz Model Graphs') xlabel('Degree of node') ylabel('Number of nodes') legend('\beta = 1.0','\beta = 0.50','\beta = 0.15','Location','NorthWest')

枢纽的形成
瓦茨-斯特罗加茨图形具有较大的集群系数,因此节点往往会形成团或较小的紧密互联的节点组。当 beta 朝其最大值 1.0 方向增加时,您会看到枢纽节点或度数相对较高的节点的数量不断增加。枢纽是其他节点之间以及图形中的团之间的常见连接。枢纽之所以存在,旨在允许形成团的同时保留平均短路径长度。
对 beta 的每个值计算平均路径长度和枢纽节点数量。就此示例而言,枢纽节点是指出入度大于或等于 55 的节点。与原始环形网格相比,这些节点的出入度全都增加了 10% 或更多。
n = 55; d = [mean(mean(distances(h))), nnz(degree(h)>=n); ... mean(mean(distances(h2))), nnz(degree(h2)>=n); ... mean(mean(distances(h3))), nnz(degree(h3)>=n); mean(mean(distances(h4))), nnz(degree(h4)>=n)]; T = table([0 0.15 0.50 1]', d(:,1), d(:,2),... 'VariableNames',{'Beta','AvgPathLength','NumberOfHubs'})
T =
4×3 table
Beta AvgPathLength NumberOfHubs
____ _____________ ____________
0 5.48 0
0.15 2.0715 20
0.5 1.9101 85
1 1.9008 92
随着 beta 的增大,图形中的平均路径长度很快减少到其极限值。这是由于形成了紧密连接的枢纽节点,枢纽节点的数量将随着 beta 的增大而变得更多。
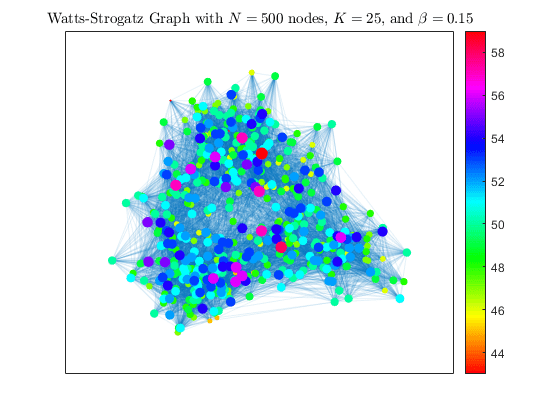
绘制  瓦茨-斯特罗加茨模型图,使每个节点的大小和颜色与其出入度成比例。这是使枢纽形成过程可视化的有效方式。
瓦茨-斯特罗加茨模型图,使每个节点的大小和颜色与其出入度成比例。这是使枢纽形成过程可视化的有效方式。
colormap hsv deg = degree(h2); nSizes = 2*sqrt(deg-min(deg)+0.2); nColors = deg; plot(h2,'MarkerSize',nSizes,'NodeCData',nColors,'EdgeAlpha',0.1) title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0.15$', ... 'Interpreter','latex') colorbar