Main Content

centrality

Measure node importance

collapse all in page

Syntax

C = centrality(G,type)
C = centrality(___,Name,Value)

Description

C = centrality(G,type) computes the node centrality specified by type for each node in the graph.

example

C = centrality(___,Name,Value) uses additional options specified by one or more Name-Value pair arguments. For example, centrality(G,'closeness','Cost',c) specifies the cost of traversing each edge.

example

Examples

collapse all

Open Live Script

Create and plot a graph containing six fictitious websites.

s = [1 1 2 2 3 3 3 4 5];
t = [2 5 3 4 4 5 6 1 1];
names = {'http://www.example.com/alpha', 'http://www.example.com/beta', ...
         'http://www.example.com/gamma', 'http://www.example.com/delta', ...
         'http://www.example.com/epsilon', 'http://www.example.com/zeta'};
G = digraph(s,t,[],names);
plot(G,'NodeLabel',{'alpha','beta','gamma','delta','epsilon','zeta'})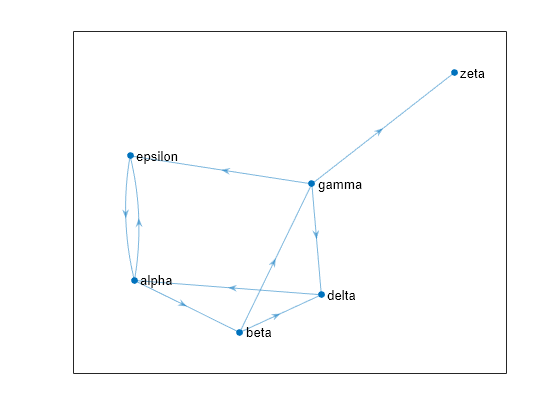

Figure contains an axes object. The axes object contains an object of type graphplot.

Calculate the page rank of each website using the centrality function. Append this information to the Nodes table of the graph as an attribute of the graph nodes.

pg_ranks = centrality(G,'pagerank')
pg_ranks = 6×1

    0.3210
    0.1706
    0.1066
    0.1368
    0.2008
    0.0643


G.Nodes.PageRank = pg_ranks;
G.Nodes
ans=6×2 table
                   Name                   PageRank
    __________________________________    ________

    {'http://www.example.com/alpha'  }    0.32098 
    {'http://www.example.com/beta'   }    0.17057 
    {'http://www.example.com/gamma'  }    0.10657 
    {'http://www.example.com/delta'  }    0.13678 
    {'http://www.example.com/epsilon'}    0.20078 
    {'http://www.example.com/zeta'   }    0.06432

Also determine which nodes are hubs and authorities using centrality and append the scores to the Nodes table.

hub_ranks = centrality(G,'hubs');
auth_ranks = centrality(G,'authorities');
G.Nodes.Hubs = hub_ranks;
G.Nodes.Authorities = auth_ranks;
G.Nodes
ans=6×4 table
                   Name                   PageRank       Hubs       Authorities
    __________________________________    ________    __________    ___________

    {'http://www.example.com/alpha'  }    0.32098        0.24995    7.3237e-05 
    {'http://www.example.com/beta'   }    0.17057        0.24995      0.099993 
    {'http://www.example.com/gamma'  }    0.10657        0.49991      0.099993 
    {'http://www.example.com/delta'  }    0.13678     9.1536e-05       0.29998 
    {'http://www.example.com/epsilon'}    0.20078     9.1536e-05       0.29998 
    {'http://www.example.com/zeta'   }    0.06432              0       0.19999
Open Live Script

Create and plot a weighted graph using a random sparse adjacency matrix. Since there are a lot of edges, use a very small value for EdgeAlpha to make the edges mostly transparent.

A = sprand(1000,1000,0.15);
A = A + A';
G = graph(A,'omitselfloops');
p = plot(G,'Layout','force','EdgeAlpha',0.005,'NodeColor','r');

Figure contains an axes object. The axes object contains an object of type graphplot.

Calculate the degree centrality of each node. Specify the importance of each edge using the edge weights.

deg_ranks = centrality(G,'degree','Importance',G.Edges.Weight);

Use discretize to place the nodes into 7 equally-spaced bins based on their centrality scores.

edges = linspace(min(deg_ranks),max(deg_ranks),7);
bins = discretize(deg_ranks,edges);

Make the size of each node in the plot proportional to its centrality score. The marker size of each node is equal to the bin number (1-7).

p.MarkerSize = bins;

Figure contains an axes object. The axes object contains an object of type graphplot.

Open Live Script

Load the data in minnesota.mat, which contains a graph object G representing the network of roads in Minnesota. The graph nodes have xy coordinates contained in the XCoord and YCoord variables of the G.Nodes table. 

load minnesota.mat
xy = [G.Nodes.XCoord G.Nodes.YCoord];

Add edge weights to the graph that roughly correspond to the length of the roads, calculated using the Euclidean distance between the xy coordinates of the end nodes of each edge.

[s,t] = findedge(G);
G.Edges.Weight = hypot(xy(s,1)-xy(t,1), xy(s,2)-xy(t,2));

Plot the graph using the xy coordinates for the nodes.

p = plot(G,'XData',xy(:,1),'YData',xy(:,2),'MarkerSize',5);
title('Minnesota Road Network')

Figure contains an axes object. The axes object with title Minnesota Road Network contains an object of type graphplot.

Compute the closeness centrality of each node. Scale the node color NodeCData to be proportional to the centrality score.

ucc = centrality(G,'closeness');
p.NodeCData = ucc;
colormap jet
colorbar
title('Closeness Centrality Scores - Unweighted')

Figure contains an axes object. The axes object with title Closeness Centrality Scores - Unweighted contains an object of type graphplot.

Also compute the weighted closeness centrality score, using the edge weights as the cost of traversing each edge. Using the road lengths as edge weights improves the score quality, since distances are now measured as the sum of the lengths of all traveled edges, rather than the number of edges traveled.

wcc = centrality(G,'closeness','Cost',G.Edges.Weight);
p.NodeCData = wcc;
title('Closeness Centrality Scores - Weighted')

Figure contains an axes object. The axes object with title Closeness Centrality Scores - Weighted contains an object of type graphplot.

Compute the weighted betweenness centrality scores for the graph to determine the roads most often found on the shortest path between two nodes. Normalize the centrality scores with the factor (n-2)(n-1)2 so that the score represents the probability that a traveler along a shortest path between two random nodes will travel through a given node. The plot indicates that there are a few very important roads leading into and out of the city.

wbc = centrality(G,'betweenness','Cost',G.Edges.Weight);
n = numnodes(G);
p.NodeCData = 2*wbc./((n-2)*(n-1));
colormap(flip(autumn,1));
title('Betweenness Centrality Scores - Weighted')

Figure contains an axes object. The axes object with title Betweenness Centrality Scores - Weighted contains an object of type graphplot.

Input Arguments

collapse all

Input graph, specified as either a graph or digraph object. Use graph to create an undirected graph or digraph to create a directed graph.

Example: G = graph(1,2)

Example: G = digraph([1 2],[2 3])

Type of node centrality, specified as one of the options in the table. The table also lists the compatible name-value arguments that work with each type. Each variety of node centrality offers a different measure of node importance in a graph.

Option

Graph type

Description

Name-Value Arguments

'degree'

Undirected

The 'degree', 'outdegree', and 'indegree' centrality types are based on the number of edges connecting to each node:

  • 'degree' — Number of edges connecting to each node. A self-loop counts as two edges connecting to the node.

  • 'indegree' — Number of incoming edges to each node. A self-loop counts as one incoming edge.

  • 'outdegree' — Number of outgoing edges from each node. A self-loop counts as one outgoing edge.

If you specify 'Importance' edge weights, then the algorithm uses the sum of the edge weights rather than the number of connecting edges.

'Importance'

'indegree'

'outdegree'

Directed

'closeness'

Undirected

The 'closeness', 'incloseness', and 'outcloseness' centrality types use the inverse sum of the distance from a node to all other nodes in the graph. If not all nodes are reachable, then the centrality of node i is:

c(i)=(A iN−1)21Ci .

Ai is the number of reachable nodes from node i (not counting i), N is the number of nodes in G, and Ci is the sum of distances from node i to all reachable nodes.

  • If no nodes are reachable from node i, then c(i) is zero.

  • For 'incloseness', the distance measure is from all nodes to node i.

  • 'Cost' edge weights specify the length of the edges.

'Cost'

'incloseness'

'outcloseness'

Directed

'betweenness'

Undirected or Directed

The 'betweenness' centrality type measures how often each graph node appears on a shortest path between two nodes in the graph. Since there can be several shortest paths between two graph nodes s and t, the centrality of node u is:

c(u)=∑s,t≠unst(u)Nst .

nst(u) is the number of shortest paths from s to t that pass through node u, and Nst is the total number of shortest paths from s to t.

  • If the graph is undirected, then the paths from s to t and from t to s count only as one path (divide the formula by two).

  • 'Cost' edge weights specify the length of the edges and help determine the shortest paths between nodes s and t.

'Cost'

'pagerank'

Undirected or Directed

The 'pagerank' centrality type results from a random walk of the network. At each node in the graph, the next node is chosen with probability 'FollowProbability' from the set of successors of the current node (neighbors for the undirected case). Otherwise, or when a node has no successors, the next node is chosen from all nodes. The centrality score is the average time spent at each node during the random walk.

  • If a node has a self-loop, then there is a chance that the algorithm traverses it. Therefore self-loops increase the pagerank centrality score of the node they attach to.

  • In multigraphs with multiple edges between the same two nodes, nodes with multiple edges are more likely to be chosen.

  • 'Importance' edge weights affect how the algorithm chooses successors. Nodes with higher importance are more likely to be chosen.

'Importance'

'FollowProbability'

'Tolerance'

'MaxIterations'

'eigenvector'

Undirected

The 'eigenvector' centrality type uses the eigenvector corresponding to the largest eigenvalue of the graph adjacency matrix. The scores are normalized such that the sum of all centrality scores is 1.

  • If there are several disconnected components, then the algorithm computes the eigenvector centrality individually for each component, then scales the scores according to the percentage of graph nodes in that component.

  • The centrality score of disconnected nodes is 1/numnodes(G).

  • Specify 'Importance' edge weights to use a weighted adjacency matrix in the calculation.

'Importance'

'Tolerance'

'MaxIterations'

'hubs'

'authorities'

Directed

The 'hubs' and 'authorities' centrality scores are two linked centrality measures that are recursive. The hubs score of a node is the sum of the authorities scores of all its successors. Similarly, the authorities score is the sum of the hubs scores of all its predecessors. The sum of all hubs scores is 1 and the sum of all authorities scores is 1.

  • These scores can be interpreted as the left (hubs) and right (authorities) singular vectors corresponding to the largest singular value of the adjacency matrix.

  • The centrality score of disconnected nodes is 1/numnodes(G).

  • Specify 'Importance' edge weights to use a weighted sum, rather than the simple sum of all successor/predecessor scores. This is equivalent to using the singular vectors of the weighted adjacency matrix.

  • If there are several disconnected components (in the weakly connected sense), then the algorithm computes the hubs and authorities scores individually for each component. The scores are then rescaled according to the percentage of graph nodes in that component so that the overall sum is still 1.

'Importance'

'Tolerance'

'MaxIterations'

Note

The centrality function assumes all edge weights are equal to 1. To change this, specify edge weights for use with the 'Cost' or 'Importance' name-value pairs.

Example: centrality(G,'degree')

Example: centrality(G,'hubs','Tolerance',tol)

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: C = centrality(G,'closeness','Cost',edgeCosts) computes the closeness centrality using edgeCosts as the cost (weight) of traversing each edge in the graph.

Cost of edge traversal, specified as the comma-separated pair consisting of 'Cost' and a vector of edge weights. The ith edge weight specifies the cost associated with traversing the edge findedge(G,i).

  • For the 'closeness', 'outcloseness', and 'incloseness' centrality types, edge costs must be nonnegative.

  • For the 'betweenness' centrality type, edge costs must be positive.

'Cost' edge weights are smaller when the connection is shorter, or faster, or cheaper. Some examples of 'Cost' edge weights are:

  • Length of a path

  • Travel time

  • Cost of a ticket

Note

'Cost' only applies to the 'closeness', 'outcloseness', 'incloseness', and 'betweenness' centrality types.

Example: centrality(G,'closeness','Cost',c)

Probability of selecting a successor node, specified as the comma-separated pair consisting of 'FollowProbability' and a scalar between 0 and 1. The follow probability is the probability that the next node selected in the traversal by the pagerank algorithm is chosen among the successors of the current node, and not at random from all nodes. For websites, this probability corresponds to clicking a link on the current web page instead of surfing to another random web page.

Note

'FollowProbability' only applies to the 'pagerank' centrality type.

Example: centrality(G,'pagerank','FollowProbability',0.5)

Edge importance, specified as the comma-separated pair consisting of 'Importance' and a vector of nonnegative edge weights. The ith edge weight specifies the importance of the edge findedge(G,i). An edge weight of zero is equivalent to removing that edge from the graph.

For multigraphs with multiple edges between two nodes, centrality adds the multiple edges together and treats them as a single edge with the combined weight.

'Importance' edge weights are larger when the connection is stronger. Some examples of 'Importance' edge weights are:

  • Number of travellers per day

  • Number of clicks on a link

  • Number of papers published together

Note

'Importance' only applies to the 'degree', 'outdegree', 'indegree', 'pagerank', 'eigenvector', 'hubs', and 'authorities' centrality types.

Example: centrality(G,'degree','Importance',x)

Maximum number of iterations, specified as the comma-separated pair consisting of 'MaxIterations' and a scalar. The centrality algorithm runs until the tolerance is met or the maximum number of iterations is reached, whichever comes first.

Note

'MaxIterations' only applies to the 'pagerank', 'eigenvector', 'hubs', and 'authorities' centrality types.

Example: centrality(G,'pagerank','MaxIterations',250)

Stopping criterion for iterative solvers, specified as the comma-separated pair consisting of 'Tolerance' and a scalar. The centrality algorithm runs until the tolerance is met or the maximum number of iterations is reached, whichever comes first.

Note

'Tolerance' only applies to the 'pagerank', 'eigenvector', 'hubs', and 'authorities' centrality types.

Example: centrality(G,'pagerank','Tolerance',1e-5)

Output Arguments

collapse all

Node centrality scores, returned as a column vector. C(i) is the centrality score of node i. The interpretation of the node centrality score depends on the type of centrality computation selected. The more central a node is, the larger its centrality score.

Extended Capabilities

Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

Version History

Introduced in R2016a

See Also

|