bctree
块割点树图
说明
示例
计算一个图的块割点树、查看生成的节点属性，然后突出显示图论图中的割点。
创建并绘制一个图。
s = [1 1 2 2 3 4 4 5 6 6 7 7 8]; t = [2 3 3 4 4 5 7 6 7 10 8 9 9]; G = graph(s,t); p = plot(G);
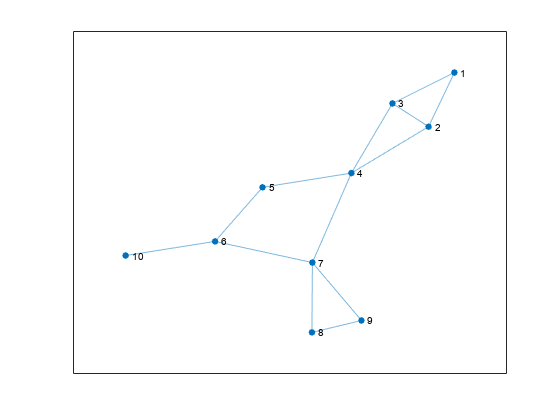
计算图的块割点树并查看节点属性。
tree = bctree(G); tree.Nodes
ans=7×3 table
IsComponent ComponentIndex CutVertexIndex
___________ ______________ ______________
true 1 0
true 2 0
true 3 0
true 4 0
false 0 4
false 0 6
false 0 7
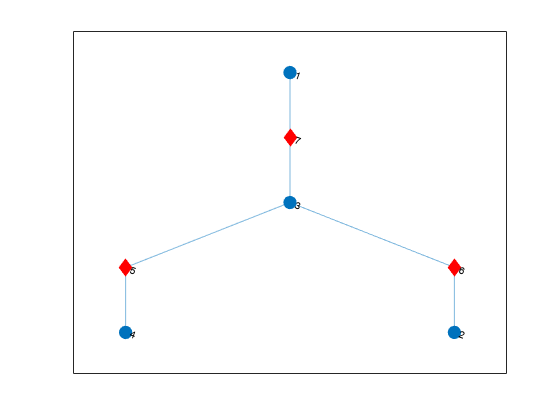
绘制块割点树，使用红色菱形标记表示代表割点的节点。圆形节点代表原图中的双连通分量。
p2 = plot(tree,'MarkerSize',9); highlight(p2,5:7,'Marker','d','NodeColor','r')
创建并绘制一个图。
s = [1 1 2 2 3 4 4 5 6 6 7 7 8]; t = [2 3 3 4 4 5 7 6 7 10 8 9 9]; G = graph(s,t); p = plot(G);
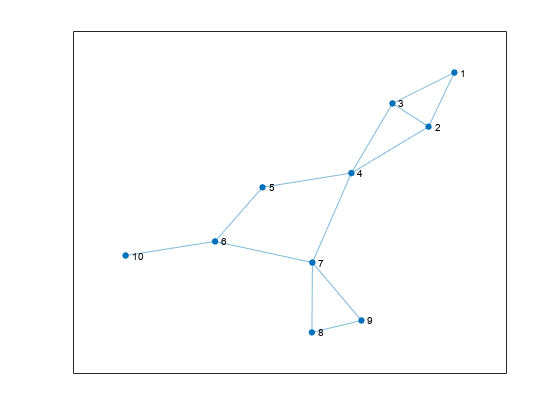
计算图的块割点树 tr，并指定第二个输出 ix 以返回节点索引。
[tr,ix] = bctree(G)
tr =
graph with properties:
Edges: [6×1 table]
Nodes: [7×3 table]
ix = 1×10
4 4 4 5 3 6 7 1 1 2
每个索引 ix(j) 指示块割点树中的一个节点，它代表输入图中的节点 j。例如，tr 中的节点 4 代表 G 中的一个分量，该分量包含节点 1、2 和 3，所以 ix 中的前三个项都是 4。
输入参数
输出参量
详细信息
图的双连通分量是指最大双连通子图。如果一个图中不包含任何割点，则它就是一个双连通图。
将一个图分解成双连通分量，可帮助我们判断该图的连通性。您可以将任何连通图分解成双连通分量树，称为块割点树。树中的各个块在共同的顶点处相连，这些顶点即为割点。
下图描绘了：
(a) 一个具有 11 个节点的无向图。
(b) 图的五个双连通分量，原图的割点通过不同颜色表示各自所属的分量。
(c) 图的块割点树，其中包含代表各个双连通分量的节点（用纯色大圆表示）和代表各个割点的节点（用多色小圆表示）。在块割点树中，每个割点与它所属的每个分量之间由一条边相连。
扩展功能
版本历史记录
在 R2016b 中推出
