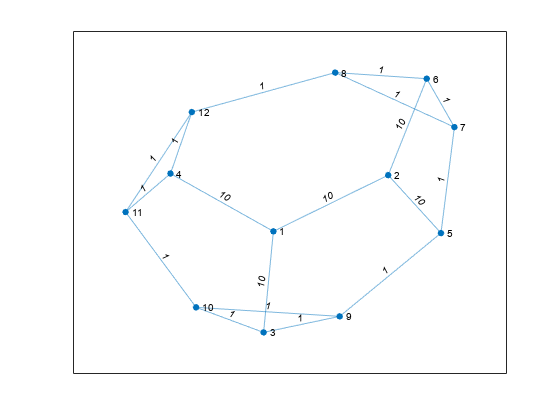
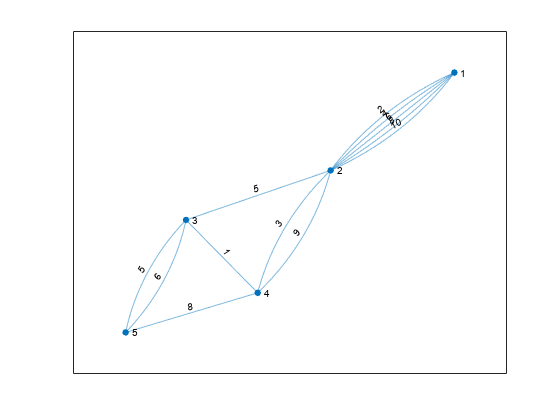
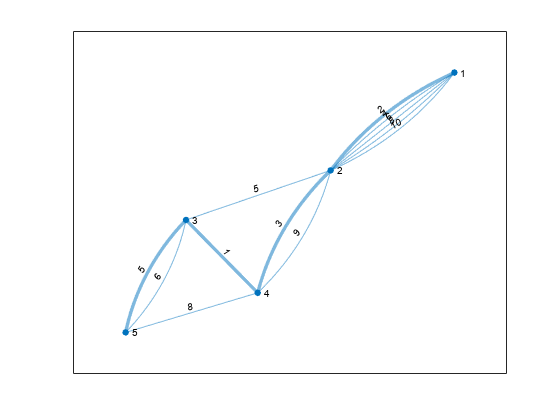
shortestpath

两个单一节点之间的最短路径

语法

P = shortestpath(G,s,t)

P = shortestpath(G,s,t,'Method',algorithm)

[P,d] = shortestpath(___)

[P,d,edgepath] = shortestpath(___)

说明

P = shortestpath(G,s,t) 计算从源节点 s 处开始到目标节点 t 处结束的最短路径。如果图进行了加权（即 G.Edges 包含变量 Weight），则这些权重用作沿图中各边的距离。否则，所有边距离都视为 1。

示例

P = shortestpath(G,s,t,'Method',algorithm) 可选择性地指定在计算最短路径时使用的算法。例如，如果 G 是加权图，则 shortestpath(G,s,t,'Method','unweighted') 将忽略 G 中的边权重，而将所有边权重视为 1。

示例

[P,d] = shortestpath(___) 支持上述语法中的任何输入参量，且可返回最短路径的长度 d。

示例

[P,d,edgepath] = shortestpath(___) 还返回从 s 到 t 的最短路径上所有边的边索引 edgepath。

示例

全部折叠

指定节点之间的最短路径

打开实时脚本

创建并绘制一个有向图。

s = [1 1 2 3 3 4 4 6 6 7 8 7 5];
t = [2 3 4 4 5 5 6 1 8 1 3 2 8];
G = digraph(s,t);
plot(G)

Figure contains an axes object. The axes object contains an object of type graphplot.

计算节点 7 和 8 之间的最短路径。

P = shortestpath(G,7,8)

P = 1×5

     7     1     3     5     8

加权图中的最短路径

打开实时脚本

创建并绘制一个具有加权边的图。

s = [1 1 1 2 2 6 6 7 7 3 3 9 9 4 4 11 11 8];
t = [2 3 4 5 6 7 8 5 8 9 10 5 10 11 12 10 12 12];
weights = [10 10 10 10 10 1 1 1 1 1 1 1 1 1 1 1 1 1];
G = graph(s,t,weights);
plot(G,'EdgeLabel',G.Edges.Weight)

Figure contains an axes object. The axes object contains an object of type graphplot.

求节点 3 和 8 之间的最短路径，并指定两个输出以同时返回该路径的长度。

[P,d] = shortestpath(G,3,8)

P = 1×5

     3     9     5     7     8

d = 
4

由于图中心的边具有较大权重，节点 3 和 8 之间的最短路径围绕边权重最小的图边界。此路径的总长度为 4。

忽略边权重的最短路径

打开实时脚本

使用自定义节点坐标创建并绘制一个具有加权边的图。

s = [1 1 1 1 1 2 2 7 7 9 3 3 1 4 10 8 4 5 6 8];
t = [2 3 4 5 7 6 7 5 9 6 6 10 10 10 11 11 8 8 11 9];
weights = [1 1 1 1 3 3 2 4 1 6 2 8 8 9 3 2 10 12 15 16];
G = graph(s,t,weights);

x = [0 0.5 -0.5 -0.5 0.5 0 1.5 0 2 -1.5 -2];
y = [0 0.5 0.5 -0.5 -0.5 2 0 -2 0 0 0];
p = plot(G,'XData',x,'YData',y,'EdgeLabel',G.Edges.Weight);

Figure contains an axes object. The axes object contains an object of type graphplot.

根据图边权重，求节点 6 和 8 之间的最短路径。以绿色突出显示此路径。

[path1,d] = shortestpath(G,6,8)

path1 = 1×5

     6     3     1     4     8

d = 
14

highlight(p,path1,'EdgeColor','g')

Figure contains an axes object. The axes object contains an object of type graphplot.

将 Method 指定为 unweighted 以忽略边权重，转而将所有边的权重都视为 1。此方法会在节点之间生成一条不同路径，该路径以前因长度太大而不能成为最短路径。以红色突出显示此路径。

[path2,d] = shortestpath(G,6,8,'Method','unweighted')

path2 = 1×3

     6     9     8

d = 
2

highlight(p,path2,'EdgeColor','r')

Figure contains an axes object. The axes object contains an object of type graphplot.

多重图中的最短路径

打开实时脚本

绘制多重图中两个节点之间的最短路径，并突出显示经过的特定边。

创建一个具有五个节点的加权多重图。有几对节点之间的边数超过一条。绘制图作为参考。

G = graph([1 1 1 1 1 2 2 3 3 3 4 4],[2 2 2 2 2 3 4 4 5 5 5 2],[2 4 6 8 10 5 3 1 5 6 8 9]);
p = plot(G,'EdgeLabel',G.Edges.Weight);

Figure contains an axes object. The axes object contains an object of type graphplot.

找出节点 1 和节点 5 之间的最短路径。由于有几个节点对之间的边数超过一条，因此为 shortestpath 指定三个输出，以返回最短路径所经过的特定边。

[P,d,edgepath] = shortestpath(G,1,5)

P = 1×5

     1     2     4     3     5

d = 
11

edgepath = 1×4

     1     7     9    10

结果表明最短路径的总长度为 11，并沿 G.Edges(edgepath,:) 指定的边前进。

G.Edges(edgepath,:)

ans=4×2 table
    EndNodes    Weight
    ________    ______

     1    2       2   
     2    4       3   
     3    4       1   
     3    5       5

通过使用 highlight 函数和 'Edges' 名称-值对组指定经过的各条边的索引来突出显示这条边路径。

highlight(p,'Edges',edgepath)

Figure contains an axes object. The axes object contains an object of type graphplot.

根据节点坐标寻找最短路径

打开实时脚本

使用节点之间的距离作为边权重来寻找图中节点之间的最短路径。

创建一个包含 10 个节点的图。

s = [1 1 2 2 3 4 4 4 5 5 6 6 7 8 9];
t = [2 4 3 5 6 5 7 9 6 7 7 8 9 10 10];
G = graph(s,t);

为图节点创建 x 和 y 坐标。然后通过指定 'XData' 和 'YData' 名称-值对组，使用节点坐标绘制图。

x = [1 2 3 2 2.5 4 3 5 3 5];
y = [1 3 4 -1 2 3.5 1 3 0 1.5];
plot(G,'XData',x,'YData',y)

Figure contains an axes object. The axes object contains an object of type graphplot.

通过计算图节点之间的欧几里德距离，为图添加边权重。根据节点坐标 $(x_{i}, y_{i})$ 计算距离，如下所示：

$d = \sqrt{{| Δ x |}^{2} + {| Δ y |}^{2}} = \sqrt{{| x_{s} - x_{t} |}^{2} + {| y_{s} - y_{t} |}^{2}} .$

要计算 $Δ x$ 和 $Δ y$ ，首先使用 findedges 获得说明图中每条边的源节点和目标节点的向量 sn 和 tn。然后使用 sn 和 tn 对 x 和 y 坐标向量进行索引，并计算 $Δ x = x_{s} - x_{t}$ 和 $Δ y = y_{s} - y_{t}$ 。hypot 函数计算平方和的平方根，因此指定 $Δ x$ 和 $Δ y$ 作为输入参量来计算每条边的长度。

[sn,tn] = findedge(G);
dx = x(sn) - x(tn);
dy = y(sn) - y(tn);
D = hypot(dx,dy);

将距离作为边权重添加到图中，并用带标签的边来重新绘制图。

G.Edges.Weight = D';
p = plot(G,'XData',x,'YData',y,'EdgeLabel',G.Edges.Weight);

Figure contains an axes object. The axes object contains an object of type graphplot.

计算节点 1 和节点 10 之间的最短路径，并指定两个输出来同时返回路径长度。对于加权图，shortestpath 自动使用考虑边权重的 'positive' 方法。

[path,len] = shortestpath(G,1,10)

path = 1×4

     1     4     9    10

len = 
6.1503

使用 highlight 函数显示图中的路径。

highlight(p,path,'EdgeColor','r','LineWidth',2)

Figure contains an axes object. The axes object contains an object of type graphplot.

输入参数

全部折叠

`G` — 输入图
`graph` 对象 | `digraph` 对象

输入图，指定为 graph 或 digraph 对象。可使用 graph 创建一个无向图，或使用 digraph 创建一个有向图。

示例: G = graph(1,2)

示例: G = digraph([1 2],[2 3])

`s,t` — 源节点 ID 和目标节点 ID（指定为单独的参量）
节点索引 | 节点名称

源节点 ID 和目标节点 ID，指定为节点索引或节点名称的单独参量。

值	示例
标量节点索引	`1`
字符向量节点名称	`'A'`
字符串标量节点名称	`"A"`

示例: shortestpath(G,2,5) 计算节点 2 和节点 5 之间的最短路径。

示例: shortestpath(G,'node1','node2') 计算命名节点 node1 和 node2 之间的最短路径。

`algorithm` — 最短路径算法
`'auto'` (默认) | `'unweighted'` | `'positive'` | `'mixed'` | `'acyclic'`

最短路径算法，指定为下表中的选项之一。

选项	描述
`'auto'`（默认值）	`'auto'` 选项会自动选择算法： `'unweighted'` 用于没有边权重的 `graph` 和 `digraph` 输入。 `'positive'` 用于具有边权重的所有 `graph` 输入，并要求权重为非负数。此选项还用于具有非负边权重的 `digraph` 输入。 `'mixed'` 用于其边权重包含某些负值的 `digraph` 输入。图不能包含负循环。
`'unweighted'`	广度优先计算，将所有边权重都视为 `1`。
`'positive'`	迪杰斯特拉算法，要求所有边权重均为非负数。
`'mixed'`（仅适用于 `digraph`）	适用于有向图的 Bellman-Ford 算法，要求图没有负循环。尽管对于相同的问题，`'mixed'` 的速度慢于 `'positive'`，但 `'mixed'` 更为通用，因为它允许某些边权重为负数。
`'acyclic'`（仅适用于 `digraph`）	算法旨在改进具有加权边的有向无环图 (DAG) 的性能。使用 `isdag` 确认有向图是否无环。

注意

对于大多数图，'unweighted' 是速度最快的算法，然后是 'acyclic'、'positive' 和 'mixed'。

示例: shortestpath(G,s,t,'Method','acyclic')

输出参量

全部折叠

`P` — 节点之间的最短路径
节点索引 | 节点名称

节点之间的最短路径，以节点索引的向量或节点名称的数组形式返回。如果节点之间没有路径，则 P 为空，即 {}。

如果 s 和 t 包含数值节点索引，则 P 是节点索引的数值向量。
如果 s 和 t 包含节点名称，则 P 是包含节点名称的元胞数组或字符串数组。

如果 s 和 t 之间有多条最短路径，则 P 只包含其中一条路径。返回的路径可能根据 Method 指定的具体算法而有所不同。

`d` — 最短路径距离
标量

最短路径距离，以数值标量形式返回。d 是 P 中连续节点之间的边权重的总和。如果节点之间没有路径，则 d 是 Inf。

`edgepath` — 最短路径上的边
边索引向量

最短路径上的边，以边索引向量形式返回。对于多重图，此输出指示两个节点之间的哪条边位于该路径上。此输出与 highlight 的 'Edges' 名称-值对组兼容，例如：highlight(p,'Edges',edgepath)。

提示

shortestpath、shortestpathtree 和 distances 函数不支持具有负边权重的无向图，或更通俗地说，不支持包含负循环的任何图，原因如下：
- 负循环是从节点出发回到自身的路径，路径上的边权重之和为负值。如果两个节点之间的路径上具有负循环，则这两个节点之间不存在最短路径，因为始终可以通过遍历负循环找到更短路径。
- 无向图中的单个负边权重会创建一个负循环。

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

名称-值参量必须为常量。
仅支持 'positive'、'unweighted' 和 'auto' 方法。
当指定节点之间没有路径时，输出 P 和 edgepath 的大小为 1×0，而不是 0×0。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

版本历史记录

在 R2015b 中推出

另请参阅

shortestpathtree | distances | nearest | graph | digraph

shortestpath

语法

说明

示例

指定节点之间的最短路径

加权图中的最短路径

忽略边权重的最短路径

多重图中的最短路径

根据节点坐标寻找最短路径

输入参数

G — 输入图 graph 对象 | digraph 对象

s,t — 源节点 ID 和目标节点 ID（指定为单独的参量） 节点索引 | 节点名称

algorithm — 最短路径算法 'auto' (默认) | 'unweighted' | 'positive' | 'mixed' | 'acyclic'

输出参量

P — 节点之间的最短路径 节点索引 | 节点名称

d — 最短路径距离 标量

edgepath — 最短路径上的边 边索引向量

提示

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

版本历史记录

另请参阅

WeChat

`G` — 输入图
`graph` 对象 | `digraph` 对象

`s,t` — 源节点 ID 和目标节点 ID（指定为单独的参量）
节点索引 | 节点名称

`algorithm` — 最短路径算法
`'auto'` (默认) | `'unweighted'` | `'positive'` | `'mixed'` | `'acyclic'`

`P` — 节点之间的最短路径
节点索引 | 节点名称

`d` — 最短路径距离
标量

`edgepath` — 最短路径上的边
边索引向量

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。