预测美国人口

此示例说明，即使使用次数最适中的多项式外插数据也是有风险且不可靠的。

此示例比 MATLAB® 出现得更早。该示例最初作为一个练习出现在福赛思、马尔科姆和莫勒尔合著的《Computer Methods for Mathematical Computations》一书中，该书由出版商 Prentice-Hall 在 1977 年出版。

现在，通过 MATLAB 可以更容易地改变参数和查看结果，但基础数学原理未变。

使用 1910 年至 2000 年的美国人口普查数据创建并绘制两个向量。

% Time interval
t = (1910:10:2000)';

% Population
p = [91.972 105.711 123.203 131.669 150.697...
    179.323 203.212 226.505 249.633 281.422]';

% Plot
plot(t,p,'bo');
axis([1910 2020 0 400]);
title('Population of the US 1910-2000');
ylabel('Millions');

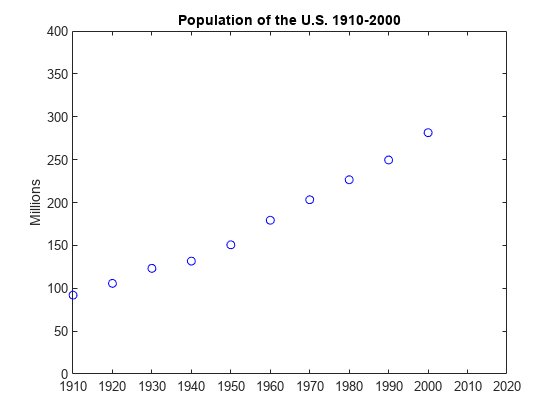
Figure contains an axes object. The axes object with title Population of the US 1910-2000, ylabel Millions contains a line object which displays its values using only markers.

那么猜想一下 2010 年美国的人口是多少？

将这些数据与 t 中的一个多项式拟合，并使用它将人口数外插到 t = 2010。通过对包含范德蒙矩阵的线性系统求解来获得多项式中的系数，该矩阵为 11×11，其元素为缩放时间的幂，即 A(i,j) = s(i)^(n-j)。

n = length(t);
s = (t-1950)/50;
A = zeros(n);
A(:,end) = 1;
for j = n-1:-1:1
   A(:,j) = s .* A(:,j+1);
end

通过对包含范德蒙矩阵最后 d+1 列的线性系统求解，获得与数据 p 拟合的 d 次多项式的系数 c：

A(:,n-d:n)*c ~= p

如果 d < 10，则方程个数多于未知数个数，并且最小二乘解是合适的。
如果 d == 10，则可以精确求解方程，而多项式实际上会对数据进行插值。

在任一种情况下，都可以使用反斜杠运算符来求解方程组。三次拟合的系数为：

c = A(:,n-3:n)\p

现在，计算从 1910 年到 2010 年每一年的多项式，然后绘制结果。

v = (1910:2020)';
x = (v-1950)/50;
w = (2010-1950)/50;
y = polyval(c,x);
z = polyval(c,w);

hold on
plot(v,y,'k-');
plot(2010,z,'ks');
text(2010,z+15,num2str(z));
hold off

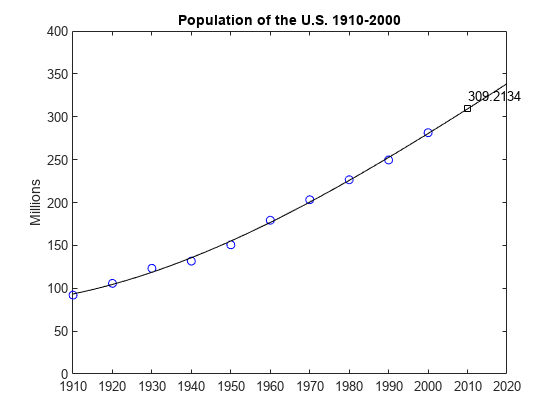
Figure contains an axes object. The axes object with title Population of the US 1910-2000, ylabel Millions contains 4 objects of type line, text. One or more of the lines displays its values using only markers

将三次拟合与四次拟合进行比较。请注意，外插点完全不同。

c = A(:,n-4:n)\p;
y = polyval(c,x);
z = polyval(c,w);

hold on
plot(v,y,'k-');
plot(2010,z,'ks');
text(2010,z-15,num2str(z));
hold off

Figure contains an axes object. The axes object with title Population of the US 1910-2000, ylabel Millions contains 7 objects of type line, text. One or more of the lines displays its values using only markers

随着阶数增加，外插变得越来越不可靠。

cla
plot(t,p,'bo')
hold on
axis([1910 2020 0 400])
colors = hsv(8);
labels = {'data'};
for d = 1:8
   [Q,R] = qr(A(:,n-d:n));
   R = R(1:d+1,:);
   Q = Q(:,1:d+1);
   c = R\(Q'*p);    % Same as c = A(:,n-d:n)\p;
   y = polyval(c,x);
   z = polyval(c,w);
   plot(v,y,'color',colors(d,:));
   plot(2010,z,'s','color',colors(d,:));
   labels{end+1} = ['degree = ' int2str(d)];
   labels{end+1} = '';
end
legend(labels, 'Location', 'NorthWest')
hold off

Figure contains an axes object. The axes object contains 17 objects of type line. One or more of the lines displays its values using only markers These objects represent data, degree = 1, degree = 2, degree = 3, degree = 4, degree = 5, degree = 6, degree = 7, degree = 8.

另请参阅

polyfit