polyfit

多项式曲线拟合

全页折叠

语法

p = polyfit(x,y,n)

[p,S] = polyfit(x,y,n)

[p,S,mu] = polyfit(x,y,n)

说明

示例

p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数，该阶数是 y 中数据的最佳拟合（基于最小二乘指标）。p 中的系数按降幂排列，p 的长度为 n+1

$p (x) = p_{1} x^{n} + p_{2} x^{n - 1} + ... + p_{n} x + p_{n + 1} .$

[p,S] = polyfit(x,y,n) 还返回一个结构体 S，后者可用作 polyval 的输入来获取误差估计值。

示例

[p,S,mu] = polyfit(x,y,n) 执行中心化和缩放以同时改善多项式和拟合算法的数值属性。此语法还返回 mu，后者是一个二元素向量，包含中心化值和缩放值。mu(1) 是 mean(x)，mu(2) 是 std(x)。使用这些值时，polyfit 将 x 的中心置于零值处并缩放为具有单位标准差

$\hat{x} = \frac{x - \bar{x}}{σ_{x}} .$

示例

全部折叠

将多项式与三角函数拟合

打开实时脚本

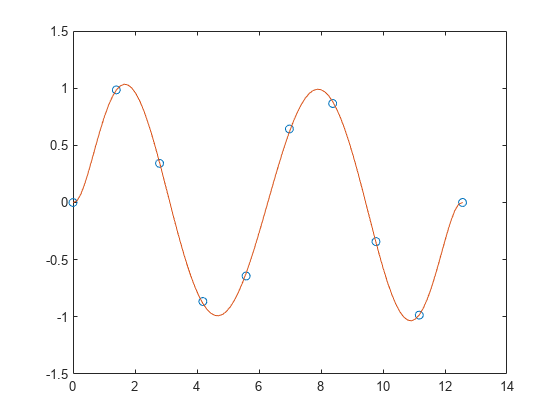
在区间 [0,4*pi] 中沿正弦曲线生成 10 个等间距的点。

x = linspace(0,4*pi,10);
y = sin(x);

使用 polyfit 将一个 7 次多项式与这些点拟合。

p = polyfit(x,y,7);

在更精细的网格上计算多项式并绘制结果图。

x1 = linspace(0,4*pi);
y1 = polyval(p,x1);
figure
plot(x,y,'o')
hold on
plot(x1,y1)
hold off

Figure contains an axes object. The axes object contains 2 objects of type line.

将多项式与点集拟合

打开实时脚本

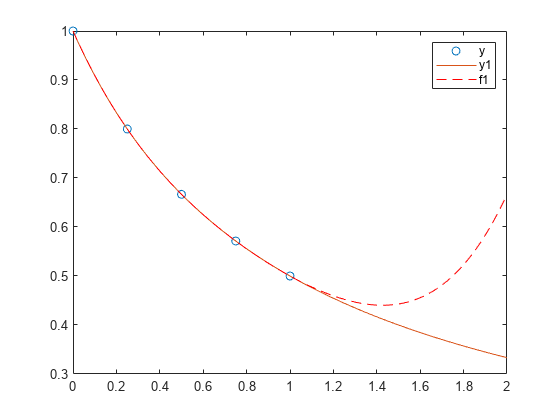
创建一个由区间 [0,1] 中的 5 个等间距点组成的向量，并计算这些点处的 $y (x) = (1 + x)^{- 1}$ 。

x = linspace(0,1,5);
y = 1./(1+x);

将 4 次多项式与 5 个点拟合。通常，对于 n 个点，可以拟合 n-1 次多项式以便完全通过这些点。

p = polyfit(x,y,4);

在由 0 和 2 之间的点组成的更精细网格上计算原始函数和多项式拟合。

x1 = linspace(0,2);
y1 = 1./(1+x1);
f1 = polyval(p,x1);

在更大的区间 [0,2] 中绘制函数值和多项式拟合，其中包含用于获取以圆形突出显示的多项式拟合的点。多项式拟合在原始 [0,1] 区间中的效果较好，但在该区间外部很快与拟合函数出现差异。

figure
plot(x,y,'o')
hold on
plot(x1,y1)
plot(x1,f1,'r--')
legend('y','y1','f1')

Figure contains an axes object. The axes object contains 3 objects of type line. These objects represent y, y1, f1.

对误差函数进行多项式拟合

打开实时脚本

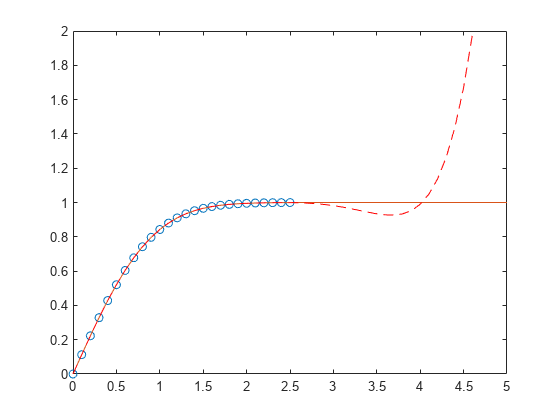
首先生成 x 点的向量，在区间 [0,2.5] 内等间距分布；然后计算这些点处的 erf(x)。

x = (0:0.1:2.5)';
y = erf(x);

确定 6 次逼近多项式的系数。

p = polyfit(x,y,6)

p = 1×7

    0.0084   -0.0983    0.4217   -0.7435    0.1471    1.1064    0.0004

为了查看拟合情况如何，在各数据点处计算多项式，并生成说明数据、拟合和误差的一个表。

f = polyval(p,x);
T = table(x,y,f,y-f,'VariableNames',{'X','Y','Fit','FitError'})

T=26×4 table
     X        Y          Fit         FitError  
    ___    _______    __________    ___________

      0          0    0.00044117    -0.00044117
    0.1    0.11246       0.11185     0.00060836
    0.2     0.2227       0.22231     0.00039189
    0.3    0.32863       0.32872    -9.7429e-05
    0.4    0.42839        0.4288    -0.00040661
    0.5     0.5205       0.52093    -0.00042568
    0.6    0.60386       0.60408    -0.00022824
    0.7     0.6778       0.67775     4.6383e-05
    0.8     0.7421       0.74183     0.00026992
    0.9    0.79691       0.79654     0.00036515
      1     0.8427       0.84238      0.0003164
    1.1    0.88021       0.88005     0.00015948
    1.2    0.91031       0.91035    -3.9919e-05
    1.3    0.93401       0.93422      -0.000211
    1.4    0.95229       0.95258    -0.00029933
    1.5    0.96611       0.96639    -0.00028097
      ⋮

在该区间中，插值与实际值非常符合。创建一个绘图，以显示在该区间以外，外插值与实际数据值如何快速偏离。

x1 = (0:0.1:5)';
y1 = erf(x1);
f1 = polyval(p,x1);
figure
plot(x,y,'o')
hold on
plot(x1,y1,'-')
plot(x1,f1,'r--')
axis([0  5  0  2])
hold off

Figure contains an axes object. The axes object contains 3 objects of type line.

使用中心化和缩放改善数值属性

打开实时脚本

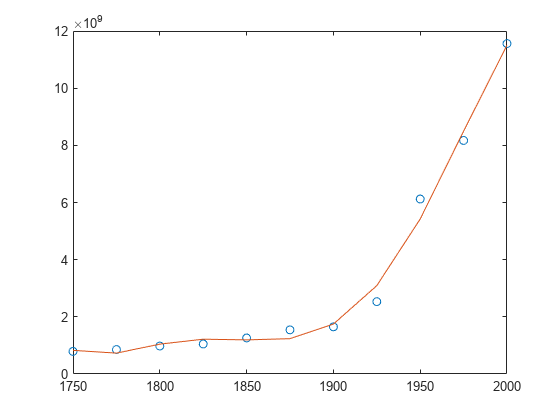
创建一个由 1750 - 2000 年的人口数据组成的表，并绘制数据点。

year = (1750:25:2000)';
pop = 1e6*[791 856 978 1050 1262 1544 1650 2532 6122 8170 11560]';
T = table(year, pop)

T=11×2 table
    year       pop   
    ____    _________

    1750     7.91e+08
    1775     8.56e+08
    1800     9.78e+08
    1825     1.05e+09
    1850    1.262e+09
    1875    1.544e+09
    1900     1.65e+09
    1925    2.532e+09
    1950    6.122e+09
    1975     8.17e+09
    2000    1.156e+10

plot(year,pop,'o')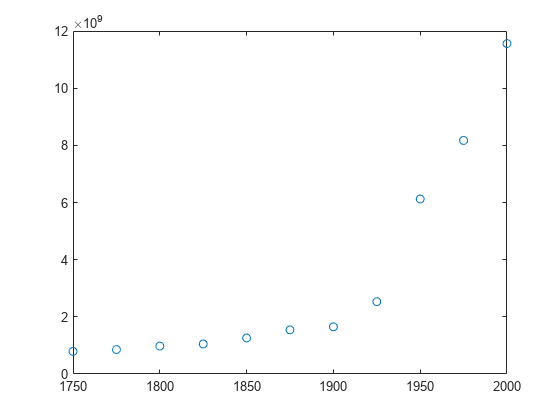

Figure contains an axes object. The axes object contains an object of type line.

使用带三个输入的 polyfit 拟合一个使用中心化和缩放的 5 次多项式，这将改善问题的数值属性。polyfit 将 year 中的数据以 0 为进行中心化，并缩放为具有标准差 1，这可避免在拟合计算中出现病态的 Vandermonde 矩阵。

[p,~,mu] = polyfit(T.year, T.pop, 5);

使用带四个输入的 polyval，根据缩放后的年份 (year-mu(1))/mu(2) 计算 p。绘制结果对原始年份的图。

f = polyval(p,year,[],mu);
hold on
plot(year,f)
hold off

Figure contains an axes object. The axes object contains 2 objects of type line.

简单线性回归

打开实时脚本

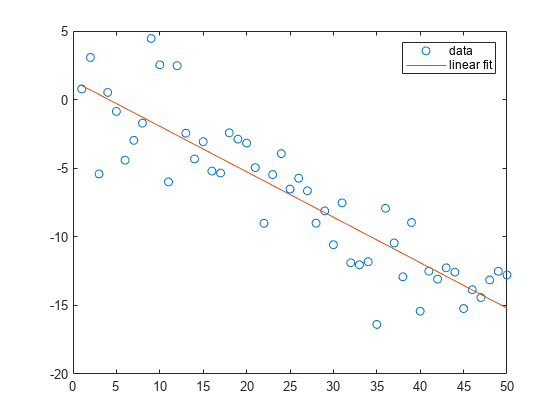
将一个简单线性回归模型与一组离散二维数据点拟合。

创建几个由样本数据点 (x,y) 组成的向量。对数据进行一次多项式拟合。

x = 1:50; 
y = -0.3*x + 2*randn(1,50); 
p = polyfit(x,y,1);

计算在 x 中的点处拟合的多项式 p。用这些数据绘制得到的线性回归模型。

f = polyval(p,x); 
plot(x,y,'o',x,f,'-') 
legend('data','linear fit')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent data, linear fit.

具有误差估计值的线性回归

打开实时脚本

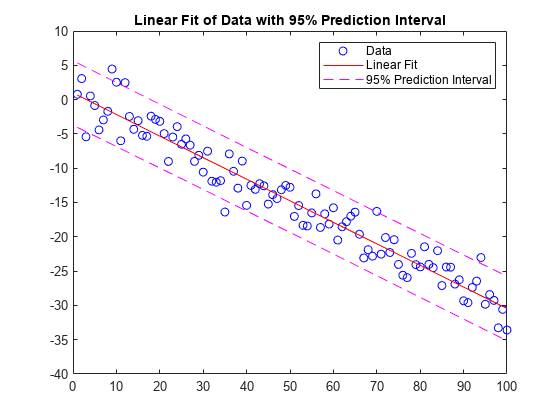
将一个线性模型拟合到一组数据点并绘制结果，其中包含预测区间为 95% 的估计值。

创建几个由样本数据点 (x,y) 组成的向量。使用 polyfit 对数据进行一次多项式拟合。指定两个输出以返回线性拟合的系数以及误差估计结构体。

x = 1:100; 
y = -0.3*x + 2*randn(1,100); 
[p,S] = polyfit(x,y,1);

计算以 p 为系数的一次多项式在 x 中各点处的拟合值。将误差估计结构体指定为第三个输入，以便 polyval 计算标准误差的估计值。标准误差估计值在 delta 中返回。

[y_fit,delta] = polyval(p,x,S);

绘制原始数据、线性拟合和 95% 预测区间 $y \pm 2 Δ$ 。

plot(x,y,'bo')
hold on
plot(x,y_fit,'r-')
plot(x,y_fit+2*delta,'m--',x,y_fit-2*delta,'m--')
title('Linear Fit of Data with 95% Prediction Interval')
legend('Data','Linear Fit','95% Prediction Interval')

Figure contains an axes object. The axes object with title Linear Fit of Data with 95% Prediction Interval contains 4 objects of type line. These objects represent Data, Linear Fit, 95% Prediction Interval.

输入参数

全部折叠

`x` — 查询点
向量

查询点，指定为一个向量。x 中的点对应于 y 中包含的拟合函数值。如果 x 不是向量，则 polyfit 将其转换为列向量 x(:)。

x 具有重复（或接近重复）的点或者如果 x 可能需要中心化和缩放时的警告消息结果。

数据类型： single | double
复数支持： 是

`y` — 查询点位置的拟合值
向量

查询点位置的拟合值，指定为向量。y 中的值对应于 x 中包含的查询点。如果 y 不是向量，则 polyfit 将其转换为列向量 y(:)。

数据类型： single | double
复数支持： 是

`n` — 多项式拟合的次数
正整数标量

多项式拟合的次数，指定为正整数标量。n 指定 p 中最左侧系数的多项式幂。

输出参数

全部折叠

`p` — 最小二乘拟合多项式系数
向量

最小二乘拟合多项式系数，以向量的形式返回。p 的长度为 n+1，包含按降幂排列的多项式系数，最高幂为 n。如果 x 或 y 包含 NaN 值且 n < length(x)，则 p 的所有元素均为 NaN。如果您指定三个输出参数来中心化和缩放数据，则与未对数据进行中心化和缩放时相比，polyfit 在 p 中返回的系数会有所不同。

使用 polyval 计算 p 在查询点处的解。

`S` — 误差估计结构体
结构体

误差估计结构体。此可选输出结构体主要用作 polyval 函数的输入，以获取误差估计值。S 包含以下字段：

字段	描述
`R`	Vandermonde 矩阵 `x` 的 QR 分解的三角 `R` 因子（可能经过置换）
`df`	自由度
`normr`	残差的范数

如果 y 中的数据是随机的，则 p 的估计协方差矩阵是 (Rinv*Rinv')*normr^2/df，其中 Rinv 是 R 的逆矩阵。

如果 y 中数据的误差呈独立正态分布，并具有常量方差，则 [y,delta] = polyval(...) 可生成至少包含 50% 的预测值的误差边界。即 y ± delta 至少包含 50% 对 x 处的未来观测值的预测值。

`mu` — 中心化值和缩放值
二元素向量

中心化值和缩放值，以二元素向量形式返回。mu(1) 为 mean(x)，mu(2) 为 std(x)。这些值以单位标准差将 x 中的查询点的中心置于零值处。

使用 mu 作为 polyval 的第四个输入以计算 p 在缩放点 (x - mu(1))/mu(2) 处的解。

局限性

在涉及很多点的问题中，使用 polyfit 增加多项式拟合的次数并不总能得到较好的拟合。高次多项式可以在数据点之间振动，导致与数据之间的拟合较差。在这些情况下，可使用低次多项式拟合（点之间倾向于更平滑）或不同的方法，具体取决于该问题。
多项式在本质上是无边界的振荡函数。所以，它们并不非常适合外插有界的数据或单调（递增或递减）的数据。

算法

polyfit 使用 x 构造具有 n+1 列和 m = length(x) 行的 Vandermonde 矩阵 V 并生成线性方程组

$(\begin{matrix} x_{1}^{n} & x_{1}^{n - 1} & \dots & 1 \\ x_{2}^{n} & x_{2}^{n - 1} & \dots & 1 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ x_{m}^{n} & x_{m}^{n - 1} & \dots & 1 \end{matrix}) (\begin{matrix} p_{1} \\ p_{2} \\ ⋮ \\ p_{n + 1} \end{matrix}) = (\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{m} \end{matrix}),$

其中 polyfit 使用 p = V\y 求解。由于 Vandermonde 矩阵中的列是向量 x 的幂，因此条件数 V 对于高阶拟合来说通常较大，生成一个奇异系数矩阵。在这些情况下，中心化和缩放可改善系统的数值属性以产生更可靠的拟合。

扩展功能

tall 数组
对行数太多而无法放入内存的数组进行计算。

用法说明和限制：

X 和 Y 必须为列向量。

有关详细信息，请参阅 tall 数组。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

请参阅Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder)。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅Run MATLAB Functions in Thread-Based Environment。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

此函数完全支持 GPU 数组。有关详细信息，请参阅Run MATLAB Functions on a GPU (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

此函数完全支持分布式数组。有关详细信息，请参阅Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

另请参阅

主题

以编程方式拟合

polyfit

语法

说明

示例

将多项式与三角函数拟合

将多项式与点集拟合

对误差函数进行多项式拟合

使用中心化和缩放改善数值属性

简单线性回归

具有误差估计值的线性回归

输入参数

x — 查询点 向量

y — 查询点位置的拟合值 向量

n — 多项式拟合的次数 正整数标量

输出参数

p — 最小二乘拟合多项式系数 向量

S — 误差估计结构体 结构体

mu — 中心化值和缩放值 二元素向量

局限性

算法

扩展功能

tall 数组 对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

另请参阅

主题

WeChat

`x` — 查询点
向量

`y` — 查询点位置的拟合值
向量

`n` — 多项式拟合的次数
正整数标量

`p` — 最小二乘拟合多项式系数
向量

`S` — 误差估计结构体
结构体

`mu` — 中心化值和缩放值
二元素向量

tall 数组
对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。