以编程方式拟合
适用于多项式模型的 MATLAB 函数
有两个 MATLAB® 函数可通过多项式对您的数据建模。
多项式拟合函数
如果您尝试对物理情况建模,务必考虑特定阶次的模型是否对您的情况有意义。
带非多项式项的线性模型
此示例说明如何使用含有非多项式项的线性模型拟合数据。
若多项式函数并未得出适合您数据的满意模型,您可尝试使用带非多项式项的线性模型。以如下函数为例,它在参数 、 和 中为线性,而在 数据中为非线性:
您可通过构建及求解一组联立方程并为参数求解,计算未知系数 、 和 。以下语法通过构建一个设计矩阵实现此目的,该矩阵中的每一列代表用于预测响应(模型中的项)的变量,每一行对应于这些变量的一个观测值。
输入 t 和 y 作为列向量。
t = [0 0.3 0.8 1.1 1.6 2.3]'; y = [0.6 0.67 1.01 1.35 1.47 1.25]';
构建设计矩阵。
X = [ones(size(t)) exp(-t) t.*exp(-t)];
计算模型系数。
a = X\y
a = 3×1
1.3983
-0.8860
0.3085
因此,该数据的模型由以下公式提供:
现在以固定间隔点评估模型,并以原始数据绘制模型。
T = (0:0.1:2.5)'; Y = [ones(size(T)) exp(-T) T.*exp(-T)]*a; plot(T,Y,'-',t,y,'o'), grid on title('Plot of Model and Original Data')
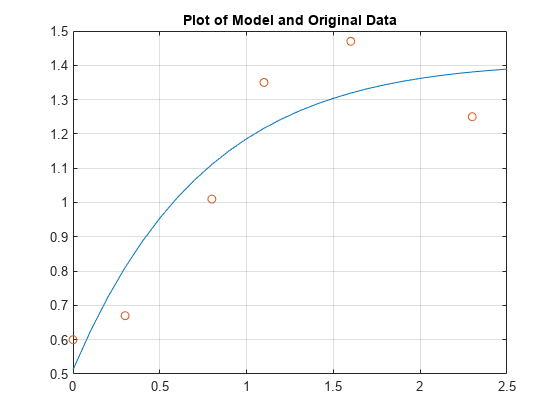
多重回归
此示例说明如何使用多重回归对具有多个预测变量的函数进行数据建模。
若 y 是具有多个预测变量的函数,则必须对表示各变量之间关系的矩阵方程进行扩展,以容纳额外的数据。这称为多重回归。
为多个 和 值测量对应的量 。将这些值分别存储在向量 x1、x2 和 y 中。
x1 = [.2 .5 .6 .8 1.0 1.1]'; x2 = [.1 .3 .4 .9 1.1 1.4]'; y = [.17 .26 .28 .23 .27 .24]';
此数据的模型采用以下形式:
多重回归可通过最大限度地减小数据与模型偏差的平方和(最小二乘拟合),对未知系数 、 和 求解。
通过构建设计矩阵 X,构建和求解一组联立方程。
X = [ones(size(x1)) x1 x2];
使用反斜杠运算符对参数求解。
a = X\y
a = 3×1
0.1018
0.4844
-0.2847
数据的最小二乘拟合模型为
为了验证该模型,请求出数据与模型偏差绝对值的最大值。
Y = X*a; MaxErr = max(abs(Y - y))
MaxErr = 0.0038
该值远小于任何数据值,表明该模型能够准确贴合数据。
以编程方式拟合
此示例说明如何使用 MATLAB 函数执行以下操作:
从 census.mat 加载样本人口普查数据,它含有 1790 年至 1990 年的美国人口数据。
load census这会向 MATLAB 工作区添加以下两个变量。
cdate是包含从 1790 年到 1990 年(以 10 为增量)的年份的列向量。pop是对应于cdate中每一年的美国人口数字的列向量。
绘制数据图。
plot(cdate,pop,'ro') title('U.S. Population from 1790 to 1990')

该图呈现出一个明显的模式,表明各变量之间存在高相关性。
计算相关系数
在示例的这一部分,您可确定变量 cdate 和 pop 之间的统计相关性,以证明数据建模的合理性。若要了解关于相关系数的详细信息,请参阅线性相关性。
计算相关系数矩阵。
corrcoef(cdate,pop)
ans = 2×2
1.0000 0.9597
0.9597 1.0000
对角矩阵元素等于 1,代表每个变量与其自身具有完美相关性。非对角矩阵非常接近 1,表明变量 cdate 和 pop 之间存在较强的统计相关性。
对数据进行多项式拟合
示例的这一部分应用 polyfit 和 polyval MATLAB 函数对数据建模。
计算拟合参数。
[p,ErrorEst] = polyfit(cdate,pop,2);
评估拟合。
pop_fit = polyval(p,cdate,ErrorEst);
绘制数据图及拟合图。
plot(cdate,pop_fit,'-',cdate,pop,'+'); title('U.S. Population from 1790 to 1990') legend('Polynomial Model','Data','Location','NorthWest'); xlabel('Census Year'); ylabel('Population (millions)');
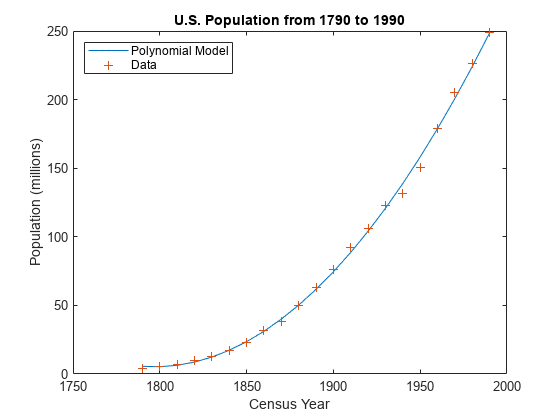
该图显示,二次多项式拟合可提供良好的数据近似度。
计算此拟合的残差。
res = pop - pop_fit; figure, plot(cdate,res,'+') title('Residuals for the Quadratic Polynomial Model')
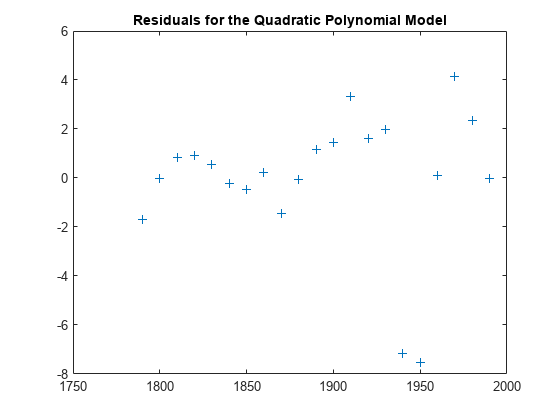
请注意,残差图显示出一种模式,该模式表示二次多项式可能不适合用于此数据的建模。
绘制和计算置信边界
置信边界是预测响应的置信区间。该区间的宽度表示拟合的确定度。
示例的这一部分将 polyfit 和 polyval 应用于 census 样本数据,为二次多项式模型产生置信边界。
以下代码使用 的区间,对应于大型样本的 95% 置信区间。
评估拟合和预测误差估计(Δ)。
[pop_fit,delta] = polyval(p,cdate,ErrorEst);
绘制数据图、拟合图和置信边界。
plot(cdate,pop,'+',... cdate,pop_fit,'g-',... cdate,pop_fit+2*delta,'r:',... cdate,pop_fit-2*delta,'r:'); xlabel('Census Year'); ylabel('Population (millions)'); title('Quadratic Polynomial Fit with Confidence Bounds') grid on
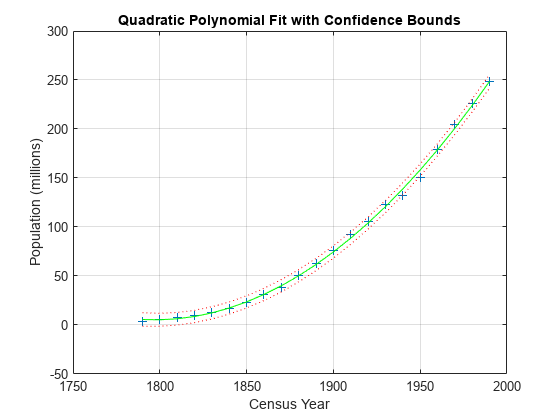
95% 区间表示新观测值有 95% 的可能性会落在范围内。