lscov
存在已知协方差情况下的最小二乘解
语法
说明
示例
为线性系统 A*x = b 创建一个矩阵 A 和向量 b。使用 lscov 计算线性系统的最小二乘解。指定三个输出参量以返回该解、其估计的标准误差和均方误差。
a1 = [0.2; 0.5; 0.6; 0.8; 1.0; 1.1]; a2 = [0.1; 0.3; 0.4; 0.9; 1.1; 1.4]; A = [ones(size(a1)) a1 a2]; b = [0.17; 0.26; 0.28; 0.23; 0.27; 0.24]; [x,stdx,mse] = lscov(A,b)
x = 3×1
0.1018
0.4844
-0.2847
stdx = 3×1
0.0058
0.0206
0.0135
mse = 1.2774e-05
向 b 添加噪声以创建采样矩阵，并使用反斜杠运算符 (\) 计算矩阵的最小二乘估计值。计算结果中每行的标准误差。
B = b + randn(6,1e5); X = A\B; s1 = std(X,0,2)
s1 = 3×1
1.6311
5.7609
3.7838
将使用反斜杠获得的标准误差与使用 lscov 获得的标准误差进行比较。按照 mse 的平方根重新缩放标准误差 stdx 以说明由 lscov 执行的缩放。X 的标准误差通常与通过 lscov 计算的标准误差相符。重新缩放后的标准误差表明，如果 b 的各元素具有均匀的噪声，则 x 的第二个元素受到的影响比第一个元素大得多。
s2 = stdx/sqrt(mse)
s2 = 3×1
1.6349
5.7661
3.7845
为问题 A*x = b 创建 A 矩阵和 b 向量。创建一个相对观测值权重向量，并计算加权最小二乘解。
a1 = [0.2; 0.5; 0.6; 0.8; 1.0; 1.1]; a2 = [0.1; 0.3; 0.4; 0.9; 1.1; 1.4]; A = [ones(size(a1)) a1 a2]; b = [0.17; 0.26; 0.28; 0.23; 0.27; 0.34]; w = [1 1 1 1 1 0.1]'; [x1,stdx1,mse1] = lscov(A,b,w)
x1 = 3×1
0.1046
0.4614
-0.2621
stdx1 = 3×1
0.0309
0.1152
0.0814
mse1 = 3.4741e-04
计算同一问题的普通最小二乘解，并绘制这两个解。对于前五个点，加权最小二乘解比普通最小二乘解更接近 b。由于加权最小二乘解的第六个元素向下加权，因此其解的第六个点离 b 更远。
[x2,stdx2,mse2] = lscov(A,b); x = 1:6; plot(x,b,"o",x,A*x1,"o",x,A*x2,"o") legend("b","Weighted","Ordinary")
为问题 A*x = b 创建 A 矩阵和 b 向量。创建一个协方差缩放矩阵，并计算广义最小二乘解。
a1 = [0.2; 0.5; 0.6; 0.8; 1.0; 1.1]; a2 = [0.1; 0.3; 0.4; 0.9; 1.1; 1.4]; A = [ones(size(a1)) a1 a2]; b = [0.17; 0.26; 0.28; 0.23; 0.27; 0.24]; C = 0.2*ones(size(a1)) + 0.8*diag(ones(size(a1))); [x,stdx,mse] = lscov(A,b,C)
x = 3×1
0.1018
0.4844
-0.2847
stdx = 3×1
0.0061
0.0206
0.0135
mse = 1.5967e-05
为问题 A*x = b 创建 A 矩阵和 b 向量。计算 x 的协方差矩阵的估计值。
a1 = [0.2; 0.5; 0.6; 0.8; 1.0; 1.1]; a2 = [0.1; 0.3; 0.4; 0.9; 1.1; 1.4]; A = [ones(size(a1)) a1 a2]; b = [0.17; 0.26; 0.28; 0.23; 0.27; 0.24]; [x,stdx,mse,S] = lscov(A,b)
x = 3×1
0.1018
0.4844
-0.2847
stdx = 3×1
0.0058
0.0206
0.0135
mse = 1.2774e-05
S = 3×3
10-3 ×
0.0341 -0.1075 0.0617
-0.1075 0.4247 -0.2712
0.0617 -0.2712 0.1829
系数标准误差等于以下协方差矩阵的对角线上值的平方根。
sqrt(diag(S))
ans = 3×1
0.0058
0.0206
0.0135
输入参数
输出参量
算法
当 m×n 矩阵 A 和 m×m 矩阵 C 在广义最小二乘问题中满秩时，这些标准公式表示在 m 大于或等于 n 时 lscov 的输出。
x = inv(A'*inv(C)*A)*A'*inv(C)*b mse = (b - A*x)'*inv(C)*(b - A*x)./(m-n) S = inv(A'*inv(C)*A)*mse stdx = sqrt(diag(S))
当 m 小于 n 时，均方误差为 0。
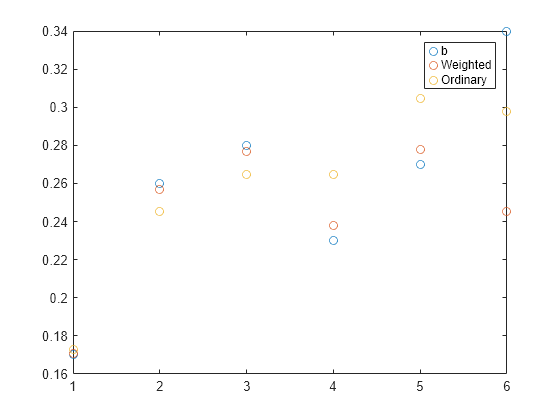
对于加权最小二乘法，当用 diag(1./w) 代替 C 时，标准公式适用。对于普通最小二乘法，用单位矩阵代替 C。
lscov 函数使用的方法比标准公式更快也更稳定，而且适用于处理秩亏情况。例如，lscov 计算乔列斯基分解 C = R'*R，然后改用 mldivide 中用于 A\b 求解最小二乘问题的相同算法求解最小二乘问题 (R'\A)*x = (R'\b)。
参考
[1] Paige, Christopher C. "Computer Solution and Perturbation Analysis of Generalized Linear Least Squares Problems." Mathematics of Computation 33, no. 145 (1979): 171–83. https://doi.org/10.2307/2006034.
[2] Golub, Gene H., and Charles F. Van Loan. Matrix Computations. Baltimore, MD: Johns Hopkins University Press, 1996.
[3] Goodall, Colin R. "Computation using the QR decomposition." Handbook of Statistics 9 (1993): 467–508. https://doi.org/10.1016/S0169-7161(05)80137-3.
[4] Strang, Gilbert. Introduction to Applied Mathematics. Wellesley, MA: Wellesley-Cambridge Press, 1986.
扩展功能
版本历史记录
在 R2006a 之前推出
