Main Content

extractIsosurface

Extract isosurface from volume using marching cubes algorithm

Since R2022b

collapse all in page

Syntax

[faces,verts] = extractIsosurface(V,isovalue)

Description

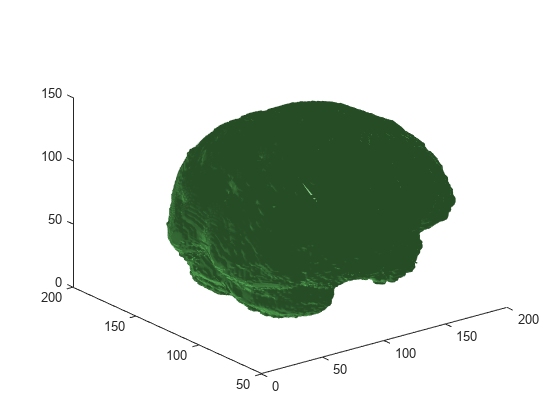
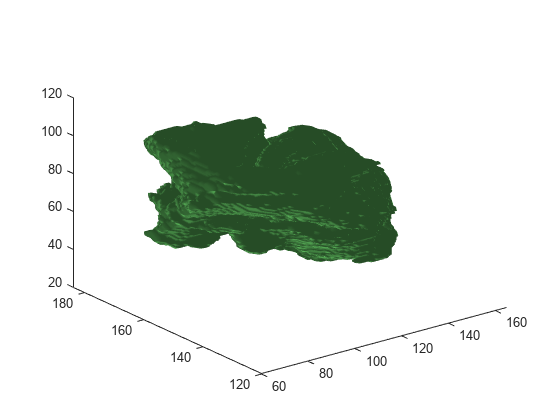
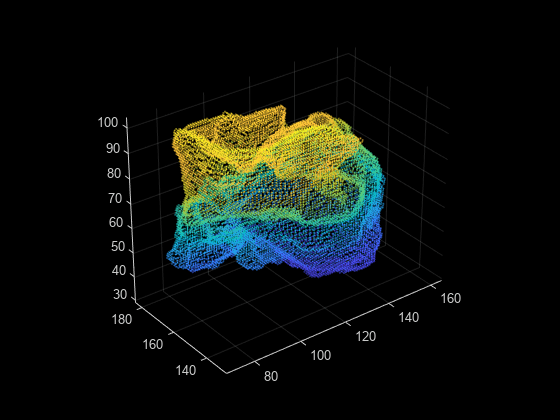
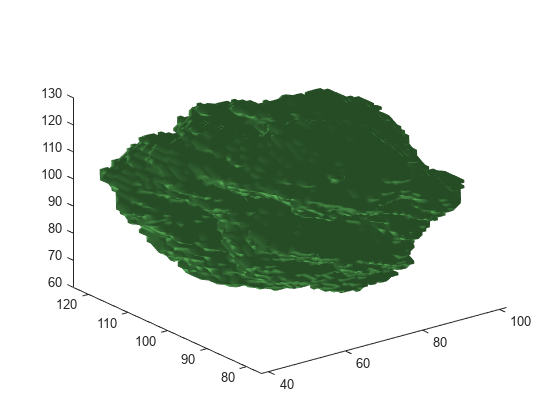
An isosurface is a 3-D surface representation of points with equal values in a 3-D intensity volume. The extractIsosurface function returns the face and vertex data of the isosurface extracted by connecting points of a constant value within a volume of space. The extractIsosurface function uses the marching cubes algorithm to extract isosurface data as arrays faster than the corresponding syntax of the isosurface function, without compromising resolution. For additional options, you must use the isosurface function.

[faces,verts] = extractIsosurface(V,isovalue) extracts an isosurface from the intensity volume V by determining where the values of V are equal to the specified isovalue isovalue. The function returns the face and vertex data of the isosurface in faces and verts, respectively.

example

Examples

collapse all

Open Live Script

Load the intensity volume data into the workspace.

load(fullfile(toolboxdir("images"),"imdata","BrainMRILabeled","images","vol_001.mat"));
V = vol;

Specify the isovalue for isosurface extraction.

isovalue = 100;

Extract the isosurface of the input volume at the specified isovalue.

[faces,verts] = extractIsosurface(V,isovalue);

Plot the extracted isosurface.

figure
p = patch(Faces=faces,Vertices=verts);
isonormals(V,p)
view(3)
set(p,FaceColor=[0.5 1 0.5])
set(p,EdgeColor="none")
camlight
lighting gouraud

Figure contains an axes object. The axes object contains an object of type patch.

This example uses:

Open Live Script

Load the intensity volume data into the workspace.

load(fullfile(toolboxdir("images"),"imdata","BrainMRILabeled","labels","label_001.mat"));
V = label;

Specify the isovalue for isosurface extraction.

isovalue = 0.05;

Extract the isosurface of the input volume at the specified isovalue.

[faces,verts] = extractIsosurface(V,isovalue);

Display and inspect the extracted isosurface.

figure
p = patch(Faces=faces,Vertices=verts);
isonormals(V,p)
view(3)
set(p,FaceColor=[0.5 1 0.5])  
set(p,EdgeColor="none")
camlight
lighting gouraud

Figure contains an axes object. The axes object contains an object of type patch.

Create a point cloud from the vertices of the extracted isosurface. Display the point cloud.

ptCloud = pointCloud(verts);
figure
pcshow(ptCloud)

Figure contains an axes object. The axes object contains an object of type scatter.

Open Live Script

Load the intensity volume data into the workspace.

load(fullfile(toolboxdir("images"),"imdata","BrainMRILabeled","labels","label_002.mat"));
V = label;

Specify the isovalue for isosurface extraction.

isovalue = 0.05;

Extract the isosurface of the input volume at the specified isovalue.

[faces,verts] = extractIsosurface(V,isovalue);

Display and inspect the extracted isosurface.

figure
p = patch(Faces=faces,Vertices=verts);
isonormals(V,p)
view(3)
set(p,FaceColor=[0.5 1 0.5])
set(p,EdgeColor="none")
camlight
lighting gouraud

Figure contains an axes object. The axes object contains an object of type patch.

Triangulate the extracted isosurface. Display the triangulation as a mesh.

T = triangulation(double(faces),double(verts));
figure
trimesh(T)

Figure contains an axes object. The axes object contains an object of type patch.

Create an STL file for 3-D printing, using the triangulation of the extracted isosurface.

stlwrite(T,"brain.stl")

Input Arguments

collapse all

Intensity volume data, specified as a 3-D numeric or logical array.

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical

Isovalue at which to compute the isosurface, specified as a numeric scalar.

Data Types: single | double

Output Arguments

collapse all

Face data of the computed isosurface, returned as an M-by-3 matrix. M is the number of faces in the isosurface. Three vertices form a triangular face. The 3-D index coordinates of all the vertices of the surface are returned as the rows of verts. Each row of the face matrix contains the row indices of the three vertices from verts that form the triangular face.

Data Types: single

Vertex data of the computed isosurface, returned as an N-by-3 matrix. N is the number of vertices in the isosurface. Each row of the matrix contains the 3-D index coordinates of one vertex of the isosurface.

Data Types: single

Algorithms

The extractIsosurface function uses the marching cubes algorithm to extract the isosurface of a volume V at the specified isovalue isovalue. The marching cubes algorithm uses lookup tables to obtain information about the faces and vertices of the isosurface. The lookup tables enable the extractIsosurface function to extract face and vertex data as arrays faster than the isosurface function without compromising resolution for large intensity volumes, such as those typically used in medical imaging. Though the purposes of extractIsosurface and isosurface are similar, there are certain differences in their implementation and output.

  • The behavior of extractIsosurface and isosurface differs for the edge case when an intensity value is equal to the specified isovalue. The isosurface function generates a surface between regions with intensities less than or equal to the isovalue and regions with intensities greater than the isovalue. The extractIsosurface function generates a surface between regions with intensities less than the isovalue and regions with intensities greater than or equal to the isovalue.

  • Except for the edge case, both extractIsosurface and isosurface generate the same number of vertices with the index coordinates of the vertices matching within a small tolerance. However, the order of the vertices in the output verts can be different.

  • Except for the edge case, both extractIsosurface and isosurface generate the same number of faces. However, the actual faces in the output faces are different because both algorithms create the same surface using different triangulations of the vertices.

References

[1] Lorensen, William E., and Harvey E. Cline. “Marching Cubes: A High Resolution 3D Surface Construction Algorithm.” ACM SIGGRAPH Computer Graphics 21, no. 4 (August 1987): 163–69. https://doi.org/10.1145/37402.37422.

Version History

Introduced in R2022b

See Also

Topics