Main Content

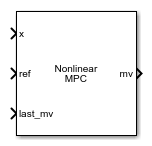
Nonlinear MPC Controller

Simulate nonlinear model predictive controllers

expand all in page
  • Nonlinear MPC Controller block

Libraries:
Model Predictive Control Toolbox

Description

The Nonlinear MPC Controller block simulates a nonlinear model predictive controller. At each control interval, the block computes optimal control moves by solving a nonlinear programming problem. For more information on nonlinear MPC, see Nonlinear MPC.

To use this block, you must first create an nlmpc object in the MATLAB® workspace.

Examples

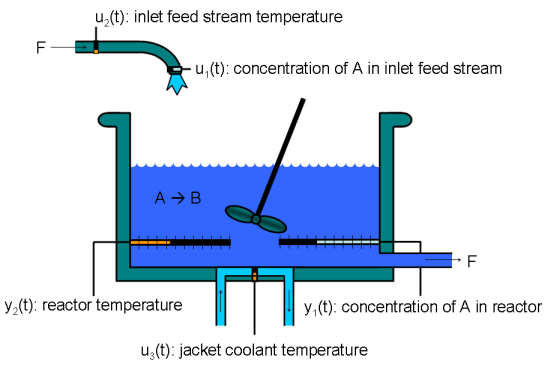
Nonlinear Model Predictive Control of Exothermic Chemical Reactor

Nonlinear Model Predictive Control of Exothermic Chemical Reactor

Control a nonlinear plant as it transitions between operating points.

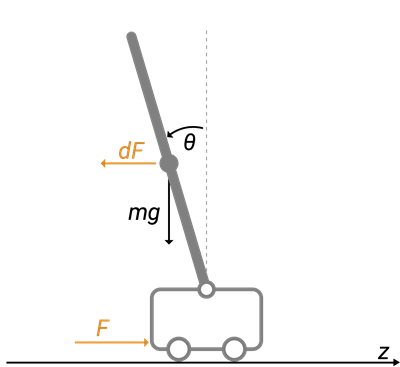
Swing-Up Control of Pendulum Using Nonlinear Model Predictive Control

Swing-Up Control of Pendulum Using Nonlinear Model Predictive Control

Achieve swing-up and balancing control of an inverted pendulum on a cart using a nonlinear model predictive controller.

Nonlinear and Gain-Scheduled MPC Control of an Ethylene Oxidation Plant

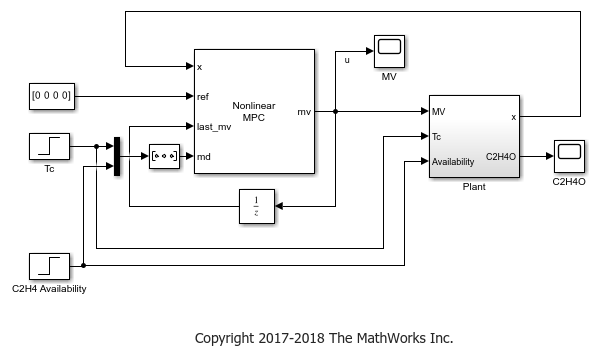
Nonlinear and Gain-Scheduled MPC Control of an Ethylene Oxidation Plant

You can generate one or more linear MPC controllers from a nonlinear MPC controller and use these controllers for gain-scheduled control applications.

Economic MPC Control of Ethylene Oxide Production

Economic MPC Control of Ethylene Oxide Production

Maximize production of an ethylene oxide plant for profit using a nonlinear cost function and nonlinear constraints.

Limitations

  • None of the Nonlinear MPC Controller block parameters are tunable.

Ports

Input

expand all

Required Inputs

Current prediction model states, specified as a vector signal of length Nx, where Nx is the number of prediction model states. Since the nonlinear MPC controller does not perform state estimation, you must either measure or estimate the current prediction model states at each control interval.

Plant output reference values, specified as a row vector signal or matrix signal.

To use the same reference values across the prediction horizon, connect ref to a row vector signal with Ny elements, where Ny is the number of output variables. Each element specifies the reference for an output variable.

To vary the references over the prediction horizon (previewing) from time k+1 to time k+p, connect ref to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the references for one prediction horizon step. If you specify fewer than p rows, the final references are used for the remaining steps of the prediction horizon.

Control signals used in plant at previous control interval, specified as a vector signal of length Nmv, where Nmv is the number of manipulated variables.

Note

Connect last_mv to the MV signals actually applied to the plant in the previous control interval. Typically, these MV signals are the values generated by the controller, though this is not always the case. For example, if your controller is offline and running in tracking mode; that is, the controller output is not driving the plant, then feeding the actual control signal to last_mv can help achieve bumpless transfer when the controller is switched back online.

Additional Inputs

If your controller prediction model has measured disturbances you must enable this port and connect to it a row vector or matrix signal.

To use the same measured disturbance values across the prediction horizon, connect md to a row vector signal with Nmd elements, where Nmd is the number of manipulated variables. Each element specifies the value for a measured disturbance.

To vary the disturbances over the prediction horizon (previewing) from time k to time k+p, connect md to a matrix signal with Nmd columns and up to p+1 rows. Here, k is the current time and p is the prediction horizon. Each row contains the disturbances for one prediction horizon step. If you specify fewer than p+1 rows, the final disturbances are used for the remaining steps of the prediction horizon.

Dependencies

To enable this port, select the Measured disturbances parameter.

If your controller uses optional parameters in its prediction model, custom cost function, or custom constraint functions, enable this input port, and connect a parameter bus signal with Np elements, where Np is the number of parameters. For more information on creating a parameter bus signal, see createParameterBus. The controller passes these parameters to its model functions, cost function, constraint functions, passivity functions and Jacobian functions.

If your controller does not use optional parameters, you must disable params.

Dependencies

To enable this port, select the Model parameters parameter.

To specify manipulated variable targets, enable this input port, and connect a vector signal. To make a given manipulated variable track its specified target value, you must also specify a nonzero tuning weight for that manipulated variable.

The supplied mv.target values at run-time apply across the prediction horizon.

Dependencies

To enable this port, select the Targets for manipulated variables parameter.

Online Constraints

To specify run-time minimum output variable constraints, enable this input port. If this port is disabled, the block uses the lower bounds specified in the OutputVariables.Min property of its controller object.

To use the same bounds over the prediction horizon, connect y.min to a row vector signal with Ny elements, where Ny is the number of outputs. Each element specifies the lower bound for an output variable.

To vary the bounds over the prediction horizon from time k+1 to time k+p, connect y.min to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Lower OV limits parameter.

To specify run-time maximum output variable constraints, enable this input port. If this port is disabled, the block uses the upper bounds specified in the OutputVariables.Min property of its controller object.

To use the same bounds over the prediction horizon, connect y.max to a row vector signal with Ny elements, where Ny is the number of outputs. Each element specifies the upper bound for an output variable.

To vary the bounds over the prediction horizon from time k+1 to time k+p, connect y.max to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Upper OV limits parameter.

To specify run-time minimum manipulated variable constraints, enable this input port. If this port is disabled, the block uses the lower bounds specified in the ManipulatedVariables.Min property of its controller object.

To use the same bounds over the prediction horizon, connect mv.min to a row vector signal with Nmv elements, where Nmv is the number of outputs. Each element specifies the lower bound for a manipulated variable.

To vary the bounds over the prediction horizon from time k to time k+p-1, connect mv.min to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Lower MV limits parameter.

To specify run-time maximum manipulated variable constraints, enable this input port. If this port is disabled, the block uses the upper bounds specified in the ManipulatedVariables.Max property of its controller object.

To use the same bounds over the prediction horizon, connect mv.max to a row vector signal with Nmv elements, where Nmv is the number of outputs. Each element specifies the upper bound for a manipulated variable.

To vary the bounds over the prediction horizon from time k to time k+p-1, connect mv.max to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Upper MV limits parameter.

To specify run-time minimum manipulated variable rate constraints, enable this input port. If this port is disabled, the block uses the lower bounds specified in the ManipulatedVariable.RateMin property of its controller object. dmv.min bounds must be nonpositive.

To use the same bounds over the prediction horizon, connect dmv.min to a row vector signal with Nmv elements, where Nmv is the number of outputs. Each element specifies the lower bound for a manipulated variable rate of change.

To vary the bounds over the prediction horizon from time k to time k+p-1, connect dmv.min to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Lower MVRate limits parameter.

To specify run-time maximum manipulated variable rate constraints, enable this input port. If this port is disabled, the block uses the upper bounds specified in the ManipulatedVariables.RateMax property of its controller object. dmv.max bounds must be nonnegative.

To use the same bounds over the prediction horizon, connect dmv.max to a row vector signal with Nmv elements, where Nmv is the number of outputs. Each element specifies the upper bound for a manipulated variable rate of change.

To vary the bounds over the prediction horizon from time k to time k+p-1, connect dmv.max to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Upper MVRate limits parameter.

To specify run-time minimum state constraints, enable this input port. If this port is disabled, the block uses the lower bounds specified in the States.Min property of its controller object.

To use the same bounds over the prediction horizon, connect x.min to a row vector signal with Nx elements, where Nx is the number of outputs. Each element specifies the lower bound for a state.

To vary the bounds over the prediction horizon from time k+1 to time k+p, connect x.min to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Lower state limits parameter.

To specify run-time maximum state constraints, enable this input port. If this port is disabled, the block uses the upper bounds specified in the States.Max property of its controller object.

To use the same bounds over the prediction horizon, connect x.max to a row vector signal with Nx elements, where Nx is the number of outputs. Each element specifies the upper bound for a state.

To vary the bounds over the prediction horizon from time k+1 to time k+p, connect x.max to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Upper state limits parameter.

Online Tuning Weights

To specify run-time output variable tuning weights, enable this input port. If this port is disabled, the block uses the tuning weights specified in the Weights.OutputVariables property of its controller object. These tuning weights penalize deviations from output references.

If the MPC controller object uses constant output tuning weights over the prediction horizon, you can specify only constant output tuning weights at runtime. Similarly, if the MPC controller object uses output tuning weights that vary over the prediction horizon, you can specify only time-varying output tuning weights at runtime.

To use constant tuning weights over the prediction horizon, connect y.wt to a row vector signal with Ny elements, where Ny is the number of outputs. Each element specifies a nonnegative tuning weight for an output variable. For more information on specifying tuning weights, see Tune Weights.

To vary the tuning weights over the prediction horizon from time k+1 to time k+p, connect y.wt to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.

Dependencies

To enable this port, select the OV weights parameter.

To specify run-time manipulated variable tuning weights, enable this input port. If this port is disabled, the block uses the tuning weights specified in the Weights.ManipulatedVariables property of its controller object. These tuning weights penalize deviations from MV targets.

To use the same tuning weights over the prediction horizon, connect mv.wt to a row vector signal with Nmv elements, where Nmv is the number of manipulated variables. Each element specifies a nonnegative tuning weight for a manipulated variable. For more information on specifying tuning weights, see Tune Weights.

To vary the tuning weights over the prediction horizon from time k to time k+p-1, connect mv.wt to a matrix signal with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.

Dependencies

To enable this port, select the MV weights parameter.

To specify run-time manipulated variable rate tuning weights, enable this input port. If this port is disabled, the block uses the tuning weights specified in the Weights.ManipulatedVariablesRate property of its controller object. These tuning weights penalize large changes in control moves.

To use the same tuning weights over the prediction horizon, connect dmv.wt to a row vector signal with Nmv elements, where Nmv is the number of manipulated variables. Each element specifies a nonnegative tuning weight for a manipulated variable rate. For more information on specifying tuning weights, see Tune Weights.

To vary the tuning weights over the prediction horizon from time k to time k+p-1, connect dmv.wt to a matrix signal with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.

Dependencies

To enable this port, select the MVRate weights parameter.

To specify a run-time slack variable tuning weight, enable this input port and connect a scalar signal. If this port is disabled, the block uses the tuning weight specified in the Weights.ECR property of its controller object.

The slack variable tuning weight has no effect unless your controller object defines soft constraints whose associated ECR values are nonzero. If there are soft constraints, increasing the ecr.wt value makes these constraints relatively harder. The controller then places a higher priority on minimizing the magnitude of the predicted worst-case constraint violation.

Dependencies

To enable this port, select the ECR weight parameter.

Initial Guesses

To specify initial guesses for the optimal manipulated variable solutions, enable this input port. If this port is disabled, the block uses the optimal control sequences calculated in the previous control interval as initial guesses.

To use the same initial guesses over the prediction horizon, connect mv.init to a vector signal with Nmv elements, where Nmv is the number of manipulated variables. Each element specifies the initial guess for a manipulated variable.

To vary the initial guesses over the prediction horizon from time k to time k+p-1, connect mv.init to a matrix signal with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the initial guesses for one prediction horizon step. If you specify fewer than p rows, the guesses in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Initial guess parameter.

To specify initial guesses for the optimal state solutions, enable this input port. If this port is disabled, the block uses the optimal state sequences calculated in the previous control interval as initial guesses.

To use the same initial guesses over the prediction horizon, connect x.init to a vector signal with Nx elements, where Nx is the number of states. Each element specifies the initial guess for a state.

To vary the initial guesses over the prediction horizon from time k to time k+p-1, connect x.init to a matrix signal with Nx columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the initial guesses for one prediction horizon step. If you specify fewer than p rows, the guesses in the final row apply for the remainder of the prediction horizon.

Dependencies

To enable this port, select the Initial guess parameter.

To specify an initial guess for the slack variable at the solution, enable this input port and connect a nonnegative scalar signal. If this port is disabled, the block uses an initial guess of 0.

Dependencies

To enable this port, select the Initial guess parameter.

Output

expand all

Required Output

Optimal manipulated variable control action, output as a column vector signal of length Nmv, where Nmv is the number of manipulated variables.

If the solver converges to a local optimum solution (nlp.status is positive), then mv contains the optimal solution.

If the solver reaches the maximum number of iterations without finding an optimal solution (nlp.status is zero) and the Optimization.UseSuboptimalSolution property of the controller is:

  • true, then mv contains the suboptimal solution

  • false, then mv is the same as last_mv

If the solver fails (nlp.status is negative), then mv is the same as last_mv.

Additional Outputs

Objective function cost, output as a nonnegative scalar signal. The cost quantifies the degree to which the controller has achieved its objectives.

The cost value is only meaningful when the nlp.status output is nonnegative.

Dependencies

To enable this port, select the Optimal cost parameter.

Slack variable, ε, used in constraint softening, output as 0 or a positive scalar value.

  • ε = 0 — All soft constraints are satisfied over the entire prediction horizon.

  • ε > 0 — At least one soft constraint is violated. When more than one constraint is violated, ε represents the worst-case soft constraint violation (scaled by the ECR values for each constraint).

Dependencies

To enable this port, select the Slack variable parameter.

Optimization status, output as one of the following:

  • Positive Integer — Solver converged to an optimal solution

  • 0 — Maximum number of iterations reached without converging to an optimal solution

  • Negative integer — Solver failed

Dependencies

To enable this port, select the Optimization status parameter.

Optimal Sequences

Optimal manipulated variable sequence, returned as a matrix signal with p+1 rows and Nmv columns, where p is the prediction horizon and Nmv is the number of manipulated variables.

The first p rows of mv.seq contain the calculated optimal manipulated variable values from current time k to time k+p-1. The first row of mv.seq contains the current manipulated variable values (output mv). Since the controller does not calculate optimal control moves at time k+p, the final two rows of mv.seq are identical.

Dependencies

To enable this port, select the Optimal control sequence parameter.

Optimal prediction model state sequence, returned as a matrix signal with p+1 rows and Nx columns, where p is the prediction horizon and Nx is the number of states.

The first row of x.seq contains the current estimated state values, either from the built-in state estimator or from the custom state estimation block input x[k|k]. The next p rows of x.seq contain the calculated optimal state values from time k+1 to time k+p.

Dependencies

To enable this port, select the Optimal state sequence parameter.

Optimal output variable sequence, returned as a matrix signal with p+1 rows and Ny columns, where p is the prediction horizon and Ny is the number of output variables.

The first p rows of y.seq contain the calculated optimal output values from current time k to time k+p-1. The first row of y.seq is computed based on the current estimated states and the current measured disturbances (first row of input md). Since the controller does not calculate optimal output values at time k+p, the final two rows of y.seq are identical.

Dependencies

To enable this port, select the Optimal output sequence parameter.

Parameters

expand all

You must provide an nlmpc object that defines a nonlinear MPC controller. To do so, enter the name of an nlmpc object in the MATLAB workspace.

Programmatic Use

Block Parameter: nlmpcobj
Type: string, character vector
Default: ""

Select this parameter to run the controller using the same sample time as its prediction model. To use a different controller sample time, clear this parameter, and specify the sample time using the Make block run at a different sample time parameter.

To limit the number of decision variables and improve computational efficiency, you can run the controller with a sample time that is different from the prediction horizon. For example, consider the case of a nonlinear MPC controller running at 10 Hz. If the plant and controller sample times match, predicting plant behavior for ten seconds requires a prediction horizon of length 100, which produces a large number of decision variables. To reduce the number of decision variables, you can use a plant sample time of 1 second and a prediction horizon of length 10.

Programmatic Use

Block Parameter: UseObjectTs
Type: string, character vector
Values: "off", "on"
Default: "on"

Specify this parameter to run the controller using a different sample time from its prediction model. Setting this parameter to -1 allows the block to inherit the sample time from its parent subsystem.

Note

The first element of the MV rate vector (which is the difference between the current and the last value of the manipulated variable) is normally weighted and constrained assuming that the last value of the MV occurred in the past at the sample time specified in the MPC object. When the block is executed with a different sample rate, this assumption no longer holds, therefore, in this case, you must make sure that the weights and constraints defined in the controller handle the first element of the MV rate vector correctly.

Dependencies

To enable this parameter, clear the Use prediction model sample time parameter.

Programmatic Use

Block Parameter: TsControl
Type: string, character vector
Default: ""

Select this parameter to simulate the controller using a MEX function generated using buildMEX. Doing so reduces the simulation time of the controller. To specify the name of the MEX function, use the Specify MEX function name parameter.

Programmatic Use

Block Parameter: UseMEX
Type: string, character vector
Values: "off", "on"
Default: "off"

Use this parameter to specify the name of the MEX function to use during simulation. To create the MEX function, use the buildMEX function.

Dependencies

To enable this parameter, select the Use MEX to speed up simulation parameter.

Programmatic Use

Block Parameter: mexname
Type: string, character vector
Default: ""

General Tab

If your controller has measured disturbances, you must select this parameter to add the md output port to the block.

Programmatic Use

Block Parameter: md_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the mv.target input port to the block.

Programmatic Use

Block Parameter: mvtarget_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

If your controller uses optional parameters, you must select this parameter to add the params output port to the block.

For more information on creating a parameter bus signal, see createParameterBus.

Programmatic Use

Block Parameter: param_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the cost output port to the block.

Programmatic Use

Block Parameter: cost_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the mv.seq output port to the block.

Programmatic Use

Block Parameter: mvseq_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the x.seq output port to the block.

Programmatic Use

Block Parameter: stateseq_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the y.seq output port to the block.

Programmatic Use

Block Parameter: ovseq_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the slack output port to the block.

Programmatic Use

Block Parameter: slack_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the nlp.status output port to the block.

Programmatic Use

Block Parameter: status_enabled
Type: string, character vector
Values: "off", "on"
Default: "off"

Online Features Tab

Select this parameter to add the ov.min input port to the block.

Programmatic Use

Block Parameter: ov_min
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the ov.max input port to the block.

Programmatic Use

Block Parameter: ov_max
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the mv.min input port to the block.

Programmatic Use

Block Parameter: mv_min
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the mv.max input port to the block.

Programmatic Use

Block Parameter: mv_max
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the dmv.min input port to the block.

Programmatic Use

Block Parameter: mvrate_min
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the dmv.max input port to the block.

Programmatic Use

Block Parameter: mvrate_max
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the x.min input port to the block.

Programmatic Use

Block Parameter: state_min
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the x.max input port to the block.

Programmatic Use

Block Parameter: state_max
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the y.wt input port to the block.

Programmatic Use

Block Parameter: ov_weight
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the mv.wt input port to the block.

Programmatic Use

Block Parameter: mv_weight
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the dmv.wt input port to the block.

Programmatic Use

Block Parameter: mvrate_weight
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the ecr.wt input port to the block.

Programmatic Use

Block Parameter: ecr_weight
Type: string, character vector
Values: "off", "on"
Default: "off"

Select this parameter to add the mv.init, x.init, and e.init input ports to the block.

Note

By default, the Nonlinar MPC Controller block uses the calculated optimal manipulated variable and state trajectories from one control interval as the initial guesses for the next control interval.

Enable the initial guess ports only if it is necessary for your application.

Programmatic Use

Block Parameter: nlp_initialize
Type: string, character vector
Values: "off", "on"
Default: "off"

Extended Capabilities

Version History

Introduced in R2018b

See Also

Blocks

Functions

Objects

Topics