Main Content

inldnl

Integral nonlinearity (INL) and differential nonlinearity (DNL) of data converters

Since R2020a

collapse all in page

Syntax

s = inldnl(analog,digital,range,type)
s = inldnl(___,Name,Value)

Description

s = inldnl(analog,digital,range,type) calculates the integral nonlinearity (INL) and differential nonlinearity (DNL) errors of ADCs and DACs. The function calculates INL and DNL using the analog and digital input output data and the nominal analog dynamic range of the converter. The function can calculate INL and DNL either using the endpoint method, or the best fit method, or using both methods.

The inldnl function only analyzes converters with a finite number of bits. That means ADCs must have saturation and quantization. The function ignores any digital value pairs that contain NaN values.

example

s = inldnl(___,Name,Value) calculates the INL and DNL errors of ADCs and DACs using one or more name-value pair arguments in addition to the input arguments in the previous syntax. Unspecified arguments take default values.

Note

Initial conditions and other anomalous data can cause this function to behave erratically. This function can analyze nonmonotonic converters, but it cannot handle multiple distinct occurrences of the same code in one transfer function.

Examples

collapse all

Open Live Script

Load the digital input and the analog output of a DAC from MAT files.

load 'digital.mat'
load 'analog.mat'

The nominal analog dynamic range of the DAC is [-1,1]. Turn on plotting for the output converter threshold. Calculate INL and DNL using both best fit and endpoint methods.

inldnl(a,d,[-1 1],'DAC','GenPlotData','on','INLMethod','All','DNLMethod','All')
INLDNL discarded 759 intervals that contained 5062 data points in total.
This made the analog value sets associated with codes [-16, -16, -16, -16, -16, -16, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -14, -14, -14, -14, -14, -14, -14, -14, -14, -14, -14, -14, -14, -14, -13, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15] contiguous.

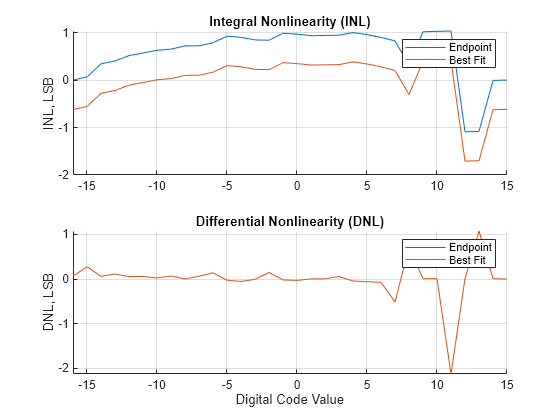
Figure contains 2 axes objects. Axes object 1 with title Integral Nonlinearity (INL), ylabel INL, LSB contains 2 objects of type line. These objects represent Endpoint, Best Fit. Axes object 2 with title Differential Nonlinearity (DNL), xlabel Digital Code Value, ylabel DNL, LSB contains 2 objects of type line. These objects represent Endpoint, Best Fit.

ans = struct with fields:
                Type: 'DAC'
               NBits: 5
                 LSB: 0.0625
        MissingCodes: [0x1 double]
               Codes: [-16 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]
    IdealCodeCenters: [-1 -0.9375 -0.8750 -0.8125 -0.7500 -0.6875 -0.6250 -0.5625 -0.5000 -0.4375 -0.3750 -0.3125 -0.2500 -0.1875 -0.1250 -0.0625 0 0.0625 0.1250 0.1875 0.2500 0.3125 0.3750 0.4375 0.5000 0.5625 0.6250 0.6875 0.7500 0.8125 0.8750 0.9375]
         CodeCenters: [-0.9522 -0.8820 -0.7987 -0.7288 -0.6557 -0.5862 -0.5165 -0.4488 -0.3785 -0.3122 -0.2421 -0.1673 -0.1028 -0.0401 0.0256 0.1009 0.1657 0.2299 0.2963 0.3627 0.4323 0.4956 0.5580 0.6195 0.6536 0.7638 0.8304 0.8970 ... ] (1x32 double)
       CodeCenterStD: [0.0246 0.0261 0.0287 0.0280 0.0254 0.0237 0.0207 0.0212 0.0175 0.0177 0.0228 0.0143 0.0106 0.0147 0.0153 0.0228 0.0079 0.0189 0.0107 0.0178 0.0144 0.0109 0.0126 0.0168 0.0116 5.7752e-06 1.1871e-05 9.4212e-06 ... ] (1x32 double)
         EndpointINL: [5.3291e-15 0.0661 0.3424 0.4027 0.5151 0.5695 0.6270 0.6522 0.7200 0.7221 0.7866 0.9252 0.8999 0.8462 0.8394 0.9862 0.9666 0.9355 0.9402 0.9447 1.0017 0.9572 0.8977 0.8240 0.3113 1.0180 1.0258 1.0338 -1.0900 ... ] (1x32 double)
          BestFitINL: [-0.6218 -0.5555 -0.2791 -0.2186 -0.1061 -0.0516 0.0061 0.0314 0.0994 0.1016 0.1663 0.3050 0.2799 0.2263 0.2196 0.3665 0.3471 0.3161 0.3210 0.3256 0.3827 0.3384 0.2790 0.2055 -0.3071 0.3997 0.4077 0.4159 -1.7078 ... ] (1x32 double)
         EndpointDNL: [0.0661 0.2763 0.0604 0.1124 0.0544 0.0575 0.0252 0.0678 0.0021 0.0645 0.1386 -0.0253 -0.0537 -0.0068 0.1468 -0.0196 -0.0311 0.0047 0.0045 0.0570 -0.0444 -0.0596 -0.0736 -0.5127 0.7067 0.0079 0.0080 -2.1238 0.0082 1.0742 0.0076 0]
          BestFitDNL: [0.0663 0.2764 0.0605 0.1125 0.0545 0.0577 0.0253 0.0680 0.0022 0.0647 0.1387 -0.0251 -0.0536 -0.0067 0.1470 -0.0195 -0.0310 0.0049 0.0047 0.0571 -0.0443 -0.0594 -0.0735 -0.5126 0.7068 0.0080 0.0081 -2.1236 0.0083 1.0743 0.0077 0]
         BestFitPoly: [0.0661 0.1440]
         OffsetError: 0.7641
     OffsetErrorUnit: 'LSB'
           GainError: 1.7843
       GainErrorUnit: 'LSB'
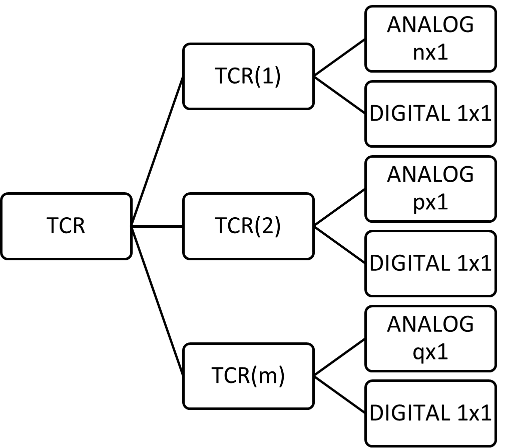
                 TCR: [1x32 struct]

Input Arguments

collapse all

  • If the device under test (DUT) is an ADC, analog input to the ADC, specified as a vector.

  • If the DUT is a DAC, analog output from the DAC, specified as a vector.

Data Types: double

  • If the device under test (DUT) is an ADC, digital output from the ADC, specified as a vector of integers.

  • If the DUT is a DAC, digital input to the DAC, specified as a vector with integer values.

Data Types: fi | single | double | int8 | int16 | int32 | uint8 | uint16 | uint32

Nominal analog dynamic range of the ADC or DAC, specified as a 2-element vector.

Data Types: double

Type of the device under test, specified as Auto, ADC, or DAC. The type determines whether to analyze the data as an ADC or DAC.

If The type is set to Auto and if the transfer function is discrete, the inldnl function analyzes the data as a DAC. The transfer function is considered as discrete if the analog data is less than half of the digital code width for each digital code.

If The type is set to Auto and if the transfer function is continuous, the inldnl function analyzes the data as an ADC.

Data Types: string

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: inldnl(a,d,[-1 1],'DAC', 'INLMethod', 'All', 'DNLMethod','All') calculates the INL and DNL of a DAC using both endpoint and best fit method.

Unit of reported offset error, specified as LSB (least significant bit), %FS (percentage full scale), FS (full scale), or all.

Note

The full scale range of the converter is defined as the difference between the last and first code on the +0.5 LSB compensated transfer curve. In a +0.5 LSB compensated transfer curve, first code is 0.5 LSB wide while the last code is 1.5 LSB wide. The input values must be considered within the full scale range of the converter.

Note

LSB is calculated by the equation LSB = Full scale range of converter2NBits.

Data Types: string

Unit of reported gain error, specified as LSB (least significant bit), %FS (percentage full scale), FS (full scale), or all.

Note

The full scale range of the converter is defined as the difference between the last and first code on the +0.5 LSB compensated transfer curve. In a +0.5 LSB compensated transfer curve, first code is 0.5 LSB wide while the last code is 1.5 LSB wide. The input values must be considered within the full scale range of the converter.

Note

LSB is calculated by the equation LSB = Full scale range of converter2NBits.

Data Types: string

Send the output data vectors of the inldnl function to the output data structure s, specified as off or on. If GenPlotData is set to on, the output data structure contains the output data vectors. The output data vectors can then be picked up by the DAC DC measurement, DAC Testbench, ADC DC Measurement, or ADC Testbench blocks to plot the DC analysis results.

Data Types: string

Method to calculate INL, specified as Endpoint, BestFit, or All.

  • If INLMethod is set to Enpoint, the inldnl function compares each threshold's position to the threshold position of an ideal converter, as determined by a line from the first code transition to the last code transition.

  • If INLMethod is set to BestFit, the inldnl function first takes the best linear fit of the ADC or DAC transfer curve. Then the function proceeds to calculate the INL using the same steps as the Enpoint method.

Data Types: string

Method to calculate DNL, specified as Endpoint, BestFit, or All.

  • If DNLMethod is set to Enpoint, the inldnl function compares each threshold's position to the threshold position of an ideal converter, as determined by a line from the first code transition to the last code transition to find the INL. The DNL is calculated from the difference between the elements of the INL vector.

  • If DNLMethod is set to BestFit, the inldnl function first takes the best linear fit of the ADC or DAC transfer curve. Then the function proceeds to calculate the DNL using the same steps as the Enpoint method.

Data Types: string

Return absolute error and full scale DNL for testing, specified as on or off. Absolute error is the total uncompensated error including offset error, gain error, and nonlinearities. In simulation, to specifically test that the measurements match the impairments, absolute error can be used instead of INL. This is because absolute error describes the entire transfer curve in a single vector.

Data Types: string

Output Arguments

collapse all

Output information of the inldnl function, returned as a structure. The output contains information about the device under test in these fields:

NameValuesDescriptionData Types
TypeADC or DACType of the device under test (DUT)string
Nbitspositive real integerResolution of the ADC or DAC DUTdouble
LSBpositive real scalarLeast significant bit value of the DUT. LSB is the smallest level the ADC can convert or the smallest increment of the DAC output.double
MissingCodesvectorMissing codes in DUT.double
Codescolumn vectorDigital codedouble
IdealCodeCenterscolumn vectorIdeal code center of the digital codedouble
CodeCenterscolumn vectorCalculated code center of the digital codedouble
CodeCenterStDcolumn vectorStandard deviation of the code center from the ideal valuedouble
EndpointINLcolumn vectorINL using Endpoint methoddouble
BestFitINLcolumn vectorINL using BestFit methoddouble
EndPointDNLcolumn vectorDNL using Endpoint methoddouble
BestFitDNLcolumn vectorDNL using BestFit methoddouble
BestFitPolyvectorPolynomial describing the best fit using standard curve-fitting technique.double
OffsetErrorreal scalarOffset error of DUTdouble
GainErrorreal scalarGain error of DUTdouble
OffsetErrorUnitLSB, %FS, or FSUnit of reported offset errorstring
GainErrorUnitLSB, %FS, or FSUnit of reported gain errorstring
TCRarray of structuresTransfer curve representation from the analog-digital pairs. For more information, see Transfer Curve Representation.struct

If you do not assign an output variable, the inldnl function also plots the transfer function of the device under test in the active figure.

Data Types: struct

More About

collapse all

Offset Error

Offset error represents the offset of the data converter transfer function curve from it ideal value at a single point. For more information, see Measuring Offset and Gain Errors in ADC.

Gain Error

Gain error represents the deviation of the slope of the data converter transfer function curve from its ideal value. For more information, see Measuring Offset and Gain Errors in ADC.

INL Error

Integral nonlinearity (INL) error, also termed as relative accuracy, is the maximum deviation of the measured transfer function from a straight line. The straight line can either be a best fit using standard curve-fitting technique, or be drawn between the endpoints of the actual transfer function after gain adjustment.

The best fit method gives a better prediction of distortion in AC applications, and a lower value of linearity error. The endpoint method is mostly used in the measurement applications of data converters, since the error budget depends on actual deviation from the ideal transfer function.

DNL Error

Differential nonlinearity (DNL) is the deviation from the ideal difference (1 LSB) between analog input levels that trigger any two successive digital output levels. The DNL error is the maximum value of DNL found at any transition.

Transfer Curve Representation

The inldnl function uses the analog-digital pairs to create a transfer curve representation (TCR) as an array of structures. Each structure has two entries: analog and digital. The analog entry is a (1×m) or (m×1) vector, and the digital entry is a scalar.

The TCR is created by ordering the analog values from least to greatest, then taking each contiguous analog range belonging to a code value and placing that range of analog values (and the corresponding digital value) in a structure in the TCR. The next structure in the TCR contains the next contiguous range of analog values belonging to a single digital code. As a result, there can be more than one structure in the TCR for any given digital code, and the TCR is ordinal.

Structure of the TCR.

The TCR for an example ADC data is shown. The corresponding TCR bin is noted in red.

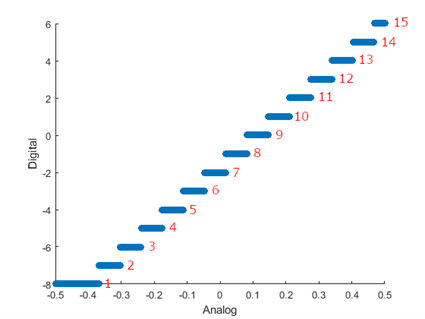
TCR for ADC data.

The process for constructing TCR is the same for monotonic or nonmonotonic converters. Once a TCR is created, the function strategically removes the duplicate bins with the smallest number until each digital code corresponds to only one bin. After reducing the TCR, the inldnl function performs analysis on the remaining data.

Version History

Introduced in R2020a

See Also

| | | |

Topics