stateSamplerGaussian
Description
The stateSamplerGaussian object creates a state sampler for motion
planning by using Gaussian distribution. Use this sampler for motion planning in narrow
passages. For information about how the Gaussian state sampler selects valid state samples,
see Find Sample States Using Gaussian State Sampler.
Creation
Syntax
Description
sampler = stateSamplerGaussianstateSpaceSE2
object with default settings.
sampler = stateSamplerGaussian(stateValidator)validatorOccupancyMap object to create a state validator, and use the state
validator as input to the Gaussian state sampler.
sampler = stateSamplerGaussian(___,Name=Value)StandardDeviation and
MaxAttempts properties as name-value arguments.
Properties
This property is read-only.
SE(2) state space, stored as an stateSpaceSE2
object. This property is set by the input state validator
stateValidator.
This property is read-only.
State validator definition, specified as a validatorOccupancyMap object or an object of a subclass of the nav.StateValidator class. This property is set by the input state validator
stateValidator.
Standard deviation for Gaussian distribution, specified as an N-element row vector. N is the number of state variables. For the SE(2) state space, the standard deviation must be a three-element row vector of form [σx σy σθ].
The object computes the default value for the standard deviation using the minimum and the maximum bounds of the state variables x, y, and θ.
Programmatically, you can read the bounds of the state variables from
the StateSpace property of the stateSamplerGaussian
object. The stateSamplerGaussian object computes the default value for the
standard deviation
as:
1/100*(sampler.StateSpace.StateBounds(:,2)-sampler.StateSpace.StateBounds(:,1))Note
For correct results, the standard deviation values must not be more than the width of the narrow passages in the configuration space.
Data Types: single | double
Threshold for the maximum number of attempts that the sampler can take to find the valid samples, specified as a positive integer. The sampler stops searching if it obtains the optimal number of valid samples before the specified threshold.
You can fine-tune this parameter value alongside the standard deviation parameter value. If the samples returned by the state sampler are scattered all over the configuration space, you can increase the number of attempts to enable the sampler to find samples that are concentrated along the obstacle boundary. Further, if you decrease the standard deviation value, you must consider increasing the maximum number of attempts to enable the sampler to find optimal samples.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Object Functions
Examples
Sample an SE(2) state space using a Gaussian state sampler, and observe the impact of the sampler parameter values on the sampling results.
Set the seed value to ensure you generate the same results.
rng(50,"twister");Create a simple occupancy map with a narrow passage.
map = binaryOccupancyMap; occupied = [5*ones(9,1),[1; 2; 3; 4; 5; 7; 8; 9; 10]]; setOccupancy(map,occupied,1); figure(Position=[0, 0, 200, 200]) show(map)
![Figure contains an axes object. The axes object with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains an object of type image.](../../examples/nav/win64/SampleSE2StateSpaceUsingGaussianStateSamplerExample_01.png)
Define the lower and upper limits of the state space variables x, y, and theta from the occupancy map.
x = map.XWorldLimits; y = map.YWorldLimits; theta = [-pi pi];
Create a state space SE(2) object using the specified state space variables. Check the validity of states in the input state space by using a state validator. Set the validation distance to 0.01.
ss = stateSpaceSE2([x; y; theta]); sv = validatorOccupancyMap(ss,Map=map); sv.ValidationDistance = 0.01;
Sample State Space Using Gaussian State Sampler
Create a Gaussian state sampler with default parameter values. By default:
The maximum number of attempts that the sampler must take for finding the state samples is set to 10.
The standard deviation values along the and directions are set to 0.1, 0.1, and 0.0628, respectively.
sampler_orig = stateSamplerGaussian(sv)
sampler_orig =
stateSamplerGaussian with properties:
StateSpace: [1×1 stateSpaceSE2]
StateValidator: [1×1 validatorOccupancyMap]
StandardDeviation: [0.1000 0.1000 0.0628]
MaxAttempts: 10
Generate 40 samples for motion planning from the input state space.
states_orig = sample(sampler_orig,40);
You can generate optimal samples by modifying the maximum number of attempts and standard deviation values. If the samples are scattered all over the input space, increase the maximum number of attempts and the standard deviation values to concentrate the state samples around the obstacle boundary.
Vary Maximum Number of Attempts
Create copies of the original state sampler object and modify the maximum number of attempts, property of the sampler, MaxAttempts, to study its impact on the sampling results. Set the standard deviation values to default values.
Set the maximum number of attempts to find valid samples to 100, and generate 40 new samples from the input state space.
sampler_2 = copy(sampler_orig); sampler_2.MaxAttempts = 100; states_2 = sample(sampler_2,40);
Set the maximum number of attempts to find valid samples to 200, and generate 40 new samples from the input state space.
sampler_3 = copy(sampler_orig); sampler_3.MaxAttempts = 200; states_3 = sample(sampler_3,40);
Display the results using the helperDisplayStates helper function. Note that, as the number of attempts increases, the samples concentrate more around the obstacle boundary.
helperDisplayStates(map,states_orig,sampler_2,states_2,sampler_3,states_3,"MaxAttempts");![Figure contains 3 axes objects and other objects of type uipanel. Axes object 1 with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 2 objects of type image, line. One or more of the lines displays its values using only markers This object represents State. Axes object 2 with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 2 objects of type image, line. One or more of the lines displays its values using only markers This object represents State. Axes object 3 with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 2 objects of type image, line. One or more of the lines displays its values using only markers This object represents State.](../../examples/nav/win64/SampleSE2StateSpaceUsingGaussianStateSamplerExample_02.png)
Vary Standard Deviation
Create copies of the original state sampler object and modify the standard deviation, property of the sampler, StandardDeviation, to study its impact on the sampling results. Set the maximum number of attempts to 200.
Generate 40 samples with the default standard deviation values.
sampler_orig.MaxAttempts = 200; states_orig = sample(sampler_orig,40);
Set the standard deviation values to [0.01 0.01 0.06]. Generate 40 new samples from the input state space.
sampler_4 = copy(sampler_orig); sampler_4.StandardDeviation = [0.01 0.01 0.06]; states_4 = sample(sampler_4,40);
Set the standard deviation values to [0.5 0.5 0.06]. Generate 40 new samples from the input state space.
sampler_5 = copy(sampler_orig); sampler_5.StandardDeviation = [0.5 0.5 0.06]; states_5 = sample(sampler_5,40);
Display the results using the helperDisplayStates helper function. Note that, as you increase the standard deviation values, the samples concentrate more around the obstacle boundary. However, if the standard deviation values are greater than the width of the narrow passages in the input space, the sampler generates incorrect results.
helperDisplayStates(map,states_orig,sampler_4,states_4,sampler_5,states_5,"Std.Deviation");![Figure contains 3 axes objects and other objects of type uipanel. Axes object 1 with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 2 objects of type image, line. One or more of the lines displays its values using only markers This object represents State. Axes object 2 with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 2 objects of type image, line. One or more of the lines displays its values using only markers This object represents State. Axes object 3 with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 2 objects of type image, line. One or more of the lines displays its values using only markers This object represents State.](../../examples/nav/win64/SampleSE2StateSpaceUsingGaussianStateSamplerExample_03.png)
Helper Function
helperDisplayStates displays results using a custom figure window.
function helperDisplayStates(map,states_orig,sampler_2,states_2,sampler_3,states_3,select) if select == "MaxAttempts" title_1 = "MaxAttempts = 10 (Default value)"; title_2 = strcat("MaxAttempts = ",num2str(sampler_2.MaxAttempts)); title_3 = strcat("MaxAttempts = ",num2str(sampler_3.MaxAttempts)); elseif select == "Std.Deviation" title_1 = "StandardDeviation = [0.1 0.1 0.06] (Default value)"; title_2 = strcat("StandardDeviation = [0.01 0.01 0.06]"); title_3 = strcat("StandardDeviation = [0.5 0.5 0.06]"); end fig_1 = figure(Position=[0 0 700 300]); movegui("center") panel_1 = uipanel(fig_1, ... Position=[0 0 0.33 1], ... Title=title_1); hPlot1 = axes(panel_1); show(map,Parent=hPlot1); hold on; plot(states_orig(:,1),states_orig(:,2),plannerLineSpec.state{:}) hold off panel_2 = uipanel(fig_1, ... Position=[0.33 0 0.33 1], ... Title=title_2); hPlot2 = axes(panel_2); show(map,Parent=hPlot2); hold on; plot(states_2(:,1),states_2(:,2),plannerLineSpec.state{:}) hold off panel_3 = uipanel(fig_1, ... Position=[0.66 0 0.33 1], ... Title=title_3); hPlot3 = axes(panel_3); show(map,Parent=hPlot3); hold on; plot(states_3(:,1),states_3(:,2),plannerLineSpec.state{:}) hold off end
Sample a state space for motion planning by using Gaussian distribution, and then use the sampled states to find an optimal path between two points in the input state space. Use a PRM path planner to compute an optimal path between two points.
Set the random number seed to ensure repeatability.
rng(100,"twister");Create Occupancy Map and Find State Variables
Load a binary map representing the input state space environment into MATLAB® workspace.
load("mapData.mat")Create an occupancy map from the input.
map = occupancyMap(narrowPassageMap);
Find the lower and upper limits of the state space variables x, y, and theta from the occupancy map.
x = map.XWorldLimits; y = map.YWorldLimits; theta = [-pi pi];
Create Gaussian State Sampler
Create a state space SE(2) object using the specified state space variables.
stateSpace = stateSpaceSE2([x; y; theta]);
Check the validity of the states in the input state space by using a state validator.
stateValidator = validatorOccupancyMap(stateSpace,Map=map);
Create a Gaussian state sampler to sample the specified state space. Set the standard deviation values.
sampler = stateSamplerGaussian(stateValidator,StandardDeviation=[25 5 0.05]);
Configure PRM Path Planner
Configure the PRM path planner. Use the Gaussian state sampler to sample the input state space.
planner = plannerPRM(stateSpace,stateValidator,StateSampler=sampler);
Find Optimal Path Between Two States
Specify the start point and the goal point in the input state space.
start = [55 50 0]; goal = [210 190 0];
Compute the optimal path between the start point and the goal point using the PRM path planner.
[path,info] = plan(planner,start,goal);
Visualize the Results
Display the occupancy map.
figure
show(map)
hold onPlot the start point and the goal point. Specify the default color and line properties for plotting the start and goal points by using the plannerLineSpec.startt and plannerLineSpec.goal functions, respectively.
plot(start(1),start(2),plannerLineSpec.start{:});
plot(goal(1),goal(2),plannerLineSpec.goal{:}); If the planner has found an optimal path between the start and goal states, plot the results. Use the plannerLineSpec.path function to specify the default color and line properties for plotting the path.
if info.IsPathFound plot(path.States(:,1),path.States(:,2),plannerLineSpec.path{:}) legend else disp("Path not found. Try modifying the planner parameters."); end
![Figure contains an axes object. The axes object with title Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 4 objects of type image, line. One or more of the lines displays its values using only markers These objects represent Start, Goal, Path.](../../examples/nav/win64/PerformMotionPlanningUsingGaussianStateSamplingExample_01.png)
More About
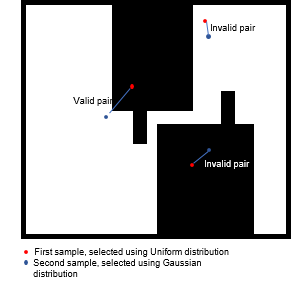
The sampler repeatedly generates pairs of states. The sampler selects the first state sample in each pair using uniform distribution, and the second state sample using Gaussian distribution centered around the first sample.
The sampler determines the distance between the first sample and second sample in each pair by using the Gaussian parameters σx, σy, and σθ.
σx specifies the spread along the x-direction
σy specifies the spread along the y-direction.
σθ specifies the spread along the angular direction.
The state validator considers a generated pair of states valid if one state sample from the pair lies on the obstacle and the other lies in the free-space. The sample from the valid pair that lies in the free-space is returned as a state sample for motion planning.
To get the optimal samples for motion planning, you can either decrease or increase the standard deviation values.
When you decrease the value of standard deviation along a particular direction, the distance between two samples in each valid pair decreases along the specified direction. Decrease the standard deviation values if the input space for motion planning has too narrow of passages. You must also increase the maximum number of attempts for the sampler to find optimal samples.
When you increase the value of standard deviation along a particular direction, the distance between two samples in each valid pair increases along the specified direction. Increase the standard deviation values if the input space for motion planning does not have too narrow of passages.
Version History
Introduced in R2023b
See Also
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)