Gesture Recognition Using Inertial Measurement Units
This example shows how to recognize gestures based on a handheld inertial measurement unit (IMU). Gesture recognition is a subfield of the general Human Activity Recognition (HAR) field. In this example, you use quaternion dynamic time warping and clustering to build a template matching algorithm to classify five gestures.
Dynamic time warping is an algorithm used to measure the similarity between two time series of data. Dynamic time warping compares two sequences, by aligning data points in the first sequence to data points in the second, neglecting time synchronization. Dynamic time warping also provides a distance metric between two unaligned sequences.
Similar to dynamic time warping, quaternion dynamic time warping compares two sequences in quaternion, or rotational, space [1].
Quaternion dynamic time warping also returns a scalar distance between two orientation trajectories. This distance metric allows you to cluster data and find a template trajectory for each gesture. You can use a set of template trajectories to recognize and classify new trajectories.
This approach of using quaternion dynamic time warping and clustering to generate template trajectories is the second level of a two-level classification system described in [2].
Gestures and Data Collection
In this example you build an algorithm that recognizes and classifies the following five gestures. Each gesture starts at the same position with the right forearm level, parallel to the floor.
up-Raise arm up, then return to level.

down - Lower arm down, then return to level.
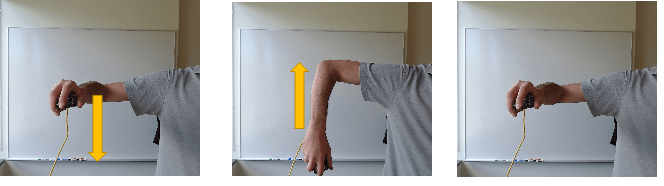
left- Swipe arm left, then return to the center. Forearm is parallel to floor for the duration.

right- Swipe arm right, then return to the center. Forearm is parallel to floor for the duration.

twist- Rotate hand 90 degrees clockwise and return to the original orientation. Forearm is parallel to the floor for the duration.

Data for these five gestures are captured using the MATLAB® Support Package for Arduino® Hardware. Four different people performed the five gestures and repeated each gesture nine to ten times. The recorded data, saved as a table, contains accelerometer and gyroscope readings, sample rate, the gesture being performed, as well as the name of person performing the gesture.
Sensor Fusion Preprocessing
The first step is to fuse all the accelerometer and gyroscope readings to produce a set of orientation time series, or trajectories. You will use the imufilter System object™ to fuse the accelerometer and gyroscope readings. The imufilter System object is available in both the Navigation Toolbox™ and the Sensor Fusion and Tracking Toolbox™. You can use a parfor loop to speed the computation. If you have Parallel Computing Toolbox™ the parfor loop will run in parallel, otherwise a regular for loop will run sequentially.
ld = load("imuGestureDataset.mat"); dataset = ld.imuGestureDataset; dataset = dataset(randperm(size(dataset,1)), :); % Shuffle the dataset Ntrials = size(dataset,1); Orientation = cell(Ntrials,1); parfor ii=1:Ntrials h = imufilter("SampleRate", dataset(ii,:).SampleRate); Orientation{ii} = h(dataset.Accelerometer{ii}, dataset.Gyroscope{ii}); end dataset = addvars(dataset, Orientation, NewVariableNames="Orientation"); gestures = string(unique(dataset.Gesture)); % Array of all gesture types people = string(unique(dataset.Who)); Ngestures = numel(gestures); Npeople = numel(people);
Quaternion Dynamic Time Warping Background
Quaternion dynamic time warping [1] compares two orientation time series in quaternion-space and formulates a distance metric composed of three parts related to the quaternion distance, derivative, and curvature. In this example, you will only compare signals based on quaternion distance.
Quaternion dynamic time warping uses time warping to compute an optimal alignment between two sequences.
The following uses quaternion dynamic time warping to compare two sequences of orientations (quaternions).
Create two random orientations:
rng(20); q = randrot(2,1);
Create two different trajectories connecting the two orientations:
h1 = 0:0.01:1; h2 = [zeros(1,10) (h1).^2]; traj1 = slerp(q(1),q(2),h1).'; traj2 = slerp(q(1),q(2),h2).';
Note that though traj1 and traj2 start and end at the same orientations, they have different lengths, and they transition along those orientations at different rates.
Next compare and find the best alignment between these two trajectories using quaternion dynamic time warping.
[qdist, idx1, idx2] = helperQDTW(traj1, traj2);
The distance metric between them is a scalar.
qdist
qdist = 1.1474
Plot the best alignment using the idx1 and idx2 variables.
e1 = eulerd(traj1, "ZYX", "frame"); e2 = eulerd(traj2, "ZYX", "frame"); figure; subplot(3,1,1); plot(e1, "-"); legend ("Yaw (Z)", "Pitch (Y)", "Roll (X)"); ylabel("traj1") subplot(3,1,2); set(gca, "ColorOrderIndex", 4); hold on; plot(e2, "-"); legend ("Yaw (Z)", "Pitch (Y)", "Roll (X)"); ylabel("traj2") hold off; subplot(3,1,3); plot(1:numel(idx1), e1(idx1,:), "-", ... 1:numel(idx2), e2(idx2,:), "o" ); title("Aligned signals"); subplot(3,1,1); title("Euler Angles for traj1 and traj2")
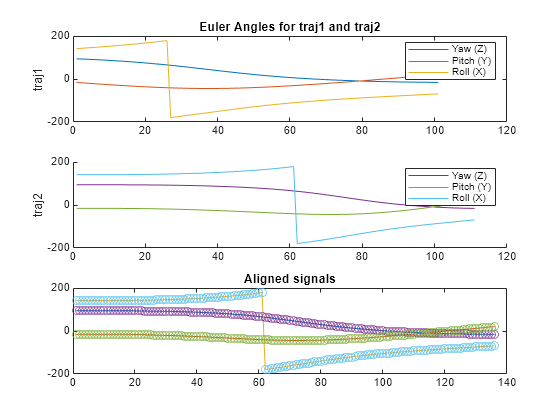
snapnow;
Training and Test Data Partitioning
The dataset contains trajectories from four test subjects. You will train your algorithm with data from three subjects and test the algorithm on the fourth subject. You repeat this process four times, each time alternating who is used for testing and who is used for training. You will produce a confusion matrix for each round of testing to see the classification accuracy.
accuracy = zeros(1,Npeople);
for pp=1:Npeople
testPerson = people(pp);
trainset = dataset(dataset.Who ~= testPerson,:);
testset = dataset(dataset.Who == testPerson,:);With the collected gesture data, you can use the quaternion dynamic time warping function to compute the mutual distances between all the recordings of a specific gesture.
% Preallocate a struct of distances and compute distances for gg=1:Ngestures gest = gestures(gg); subdata = trainset(trainset.Gesture == gest,:); Nsubdata = size(subdata,1); D = zeros(Nsubdata); traj = subdata.Orientation; parfor ii=1:Nsubdata for jj=1:Nsubdata if jj > ii % Only calculate triangular matrix D(ii,jj) = helperQDTW(traj{ii}, traj{jj}); end end end allgestures.(gest) = traj; dist.(gest) = D + D.'; % Render symmetric matrix to get all mutual distances end
Clustering and Templating
The next step is to generate template trajectories for each gesture. The structure dist contains the mutual distances between all pairs of recordings for a given gesture. In this section, you cluster all trajectories of a given gesture based on mutual distance. The function helperClusterWithSplitting uses a cluster splitting approach described in [2]. All trajectories are initially placed in a single cluster. The algorithm splits the cluster if the radius of the cluster (the largest distance between any two trajectories in the cluster) is greater than the radiusLimit.
The splitting process continues recursively for each cluster. Once a median is found for each cluster, the trajectory associated with that cluster is saved as a template for that particular gesture. If the ratio of the number of trajectories in the cluster to the total number of trajectories of a given gesture is less than clusterMinPct, the cluster is discarded. This prevents outlier trajectories from negatively affecting the classification process. Depending on choice of radiusLimit and clusterMinPct a gesture may have one or several clusters, and hence may have one or several templates.
radiusLimit = 60;
clusterMinPct = 0.2;
parfor gg=1:Ngestures
gest = gestures(gg);
Dg = dist.(gest); %#ok<*PFBNS>
[gclusters, gtemplates] = helperClusterWithSplitting(Dg, radiusLimit);
clusterSizes = cellfun(@numel, gclusters, "UniformOutput", true);
totalSize = sum(clusterSizes);
clusterPct = clusterSizes./totalSize;
validClusters = clusterPct > clusterMinPct;
tidx = gtemplates(validClusters);
tmplt = allgestures.(gest)(tidx);
templateTraj{gg} = tmplt;
labels{gg} = repmat(gest, numel(tmplt),1);
end
templates = table(vertcat(templateTraj{:}), vertcat(labels{:}));
templates.Properties.VariableNames = ["Orientation", "Gesture"];The template variable is stored as a table. Each row contains a template trajectory stored in the Orientation variable and an associated gesture label stored in the Gesture variable. You will use this set of templates to recognize new gestures in the testset.
Classification System
Using quaternion dynamic time warping, compare the new gesture data from the test set can be compared to each of the gesture template. The system classifies the new unknown gesture as the class of the template that has the smallest quaternion dynamic time warping distance to the unknown gesture. If the distance to each template is beyond the radiusLimit, the test gesture is marked as unrecognized.
Ntest = size(testset,1);
Ntemplates = size(templates,1);
testTraj = testset.Orientation;
expected = testset.Gesture;
actual = strings(size(expected));
parfor ii=1:Ntest
testdist = zeros(1,Ntemplates);
for tt=1:Ntemplates
testdist(tt) = helperQDTW(testTraj{ii}, templates.Orientation{tt});
end
[mind, mindidx] = min(testdist);
if mind > radiusLimit
actual(ii) = "unrecognized";
else
actual(ii) = templates.Gesture{mindidx};
end
end
results.(testPerson).actual = actual;
results.(testPerson).expected = expected;
end
Compute the accuracy of the system in identifying gestures in the test set and generate a confusion matrix.
for pp=1:Npeople figure; act = results.(people(pp)).actual; exp = results.(people(pp)).expected; numCorrect = sum(act == exp); Ntest = numel(act); accuracy = 100 * numCorrect./Ntest; confusionchart([exp; "unrecognized"], [act; missing]); title("Test subject = " + people(pp) + newline + "Accuracy = " + accuracy + "%" ); end snapnow;

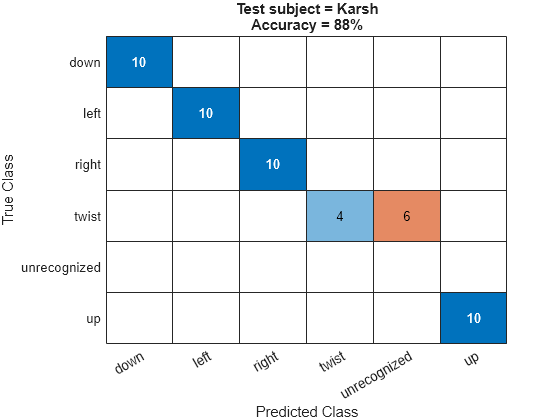
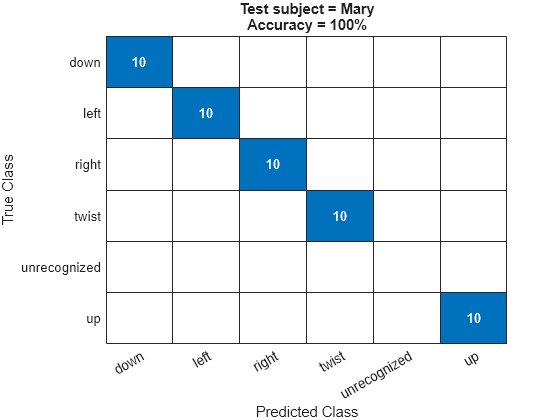
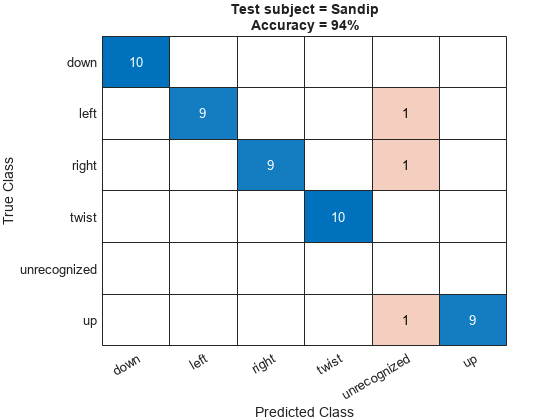
The average accuracy across all four test subject configurations is above 90%.
AverageAccuracy = mean(accuracy)
AverageAccuracy = 94
Conclusion
By fusing IMU data with the imufilter object and using quaternion dynamic time warping to compare a gesture trajectory to a set of template trajectories you recognize gestures with high accuracy. You can use sensor fusion along with quaternion dynamic time warping and clustering to construct an effective gesture recognition system.
References
[1] B. Jablonski, "Quaternion Dynamic Time Warping," in IEEE Transactions on Signal Processing, vol. 60, no. 3, March 2012.
[2] R. Srivastava and P. Sinha, "Hand Movements and Gestures Characterization Using Quaternion Dynamic Time Warping Technique," in IEEE Sensors Journal, vol. 16, no. 5, March 1, 2016.