使用解析黑塞函数的 `fmincon` 内点算法

此示例说明如何使用导数信息来使求解过程更快、更稳健。fmincon 内点算法可以接受黑塞函数作为输入。当您提供黑塞函数时，您可以更快得到约束最小化问题更为准确的解。

辅助函数 bigtoleft 是一个目标函数，随着 x(1) 坐标变为负值，该函数迅速变为负值。它的梯度是三元素向量。bigtoleft 辅助函数的代码出现在此示例末尾。

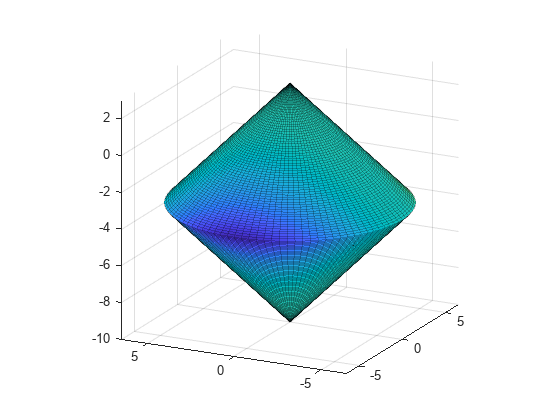
此示例的约束集是两个圆锥体（一个尖端向上，一个尖端向下）内部的交集。约束函数是一个双分量向量，每个圆锥体包含一个分量。一个由于此示例是三维的，约束的梯度是一个 3×2 矩阵。twocone 辅助函数的代码出现在此示例末尾。

创建一个约束图窗，使用目标函数进行着色。

% Create figure
figure1 = figure;

% Create axes
axes1 = axes('Parent',figure1);
view([-63.5 18]);
grid('on');
hold('all');

% Set up polar coordinates and two cones
r=0:.1:6.5;
th=2*pi*(0:.01:1);
x=r'*cos(th);
y=r'*sin(th);
z=-10+sqrt(x.^2+y.^2);
zz=3-sqrt(x.^2+y.^2);

% Evaluate objective function on cone surfaces
newxf=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000;
newxg=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000;

% Create lower surf with color set by objective
surf(x,y,z,newxf,'Parent',axes1,'EdgeAlpha',0.25);

% Create upper surf with color set by objective
surf(x,y,zz,newxg,'Parent',axes1,'EdgeAlpha',0.25);
axis equal

创建黑塞函数

要在 fmincon 求解器中使用二阶导数信息，您必须创建一个黑塞矩阵，它是拉格朗日乘数的黑塞矩阵。拉格朗日函数的黑塞矩阵由以下方程给出

$\nabla_{x x}^{2} L (x, λ) = \nabla^{2} f (x) + \sum λ_{i} \nabla^{2} c_{i} (x) + \sum λ_{i} \nabla^{2} c e q_{i} (x) .$

此处， $f (x)$ 是 bigtoleft 函数， $c_{i} (x)$ 是两个锥约束函数。位于此示例末尾的 hessinterior 辅助函数使用拉格朗日乘数结构体 lambda 计算在点 x 处的拉格朗日函数的黑塞矩阵。该函数首先计算 $\nabla^{2} f (x)$ 。然后，它计算两个约束：黑塞 $\nabla^{2} c_{1} (x)$ 和 $\nabla^{2} c_{2} (x)$ ，将它们乘以对应的拉格朗日乘数 lambda.ineqnonlin(1) 和 lambda.ineqnonlin(2)，并将它们相加。从 twocone 约束函数的定义可以看出 $\nabla^{2} c_{1} (x) = \nabla^{2} c_{2} (x)$ ，这可以简化计算。

设置选项以使用导数

要使 fmincon 能够使用目标梯度、约束梯度和黑塞矩阵，您必须设置适当的选项。使用拉格朗日乘数的黑塞矩阵的 HessianFcn 选项仅适用于内点算法。

options = optimoptions('fmincon','Algorithm','interior-point',...
    "SpecifyConstraintGradient",true,"SpecifyObjectiveGradient",true,...
    'HessianFcn',@hessinterior);

使用所有导数信息进行最小化

设置初始点 x0 = [-1,-1,-1]。

x0 = [-1,-1,-1];

该问题没有线性约束或边界。将这些参量设置为 []。

A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];

求解。

[x,fval,eflag,output] = fmincon(@bigtoleft,x0,...
           A,b,Aeq,beq,lb,ub,@twocone,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

检查解和求解过程

检查解、目标函数值、退出标志以及函数计算和迭代的次数。

disp(x)

   -6.5000   -0.0000   -3.5000

disp(fval)

  -2.8941e+03

disp(eflag)

disp([output.funcCount,output.iterations])

     7     6

如果您不使用黑塞函数，fmincon 需要更多次迭代才能收敛，并且需要更多函数计算。

options.HessianFcn = [];
[x2,fval2,eflag2,output2] = fmincon(@bigtoleft,x0,...
           A,b,Aeq,beq,lb,ub,@twocone,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

disp([output2.funcCount,output2.iterations])

    13     9

如果您也未提供梯度信息，fmincon 会执行相同次数的迭代，但要求进行更多函数计算。

options.SpecifyConstraintGradient = false;
options.SpecifyObjectiveGradient = false;
[x3,fval3,eflag3,output3] = fmincon(@bigtoleft,x0,...
           A,b,Aeq,beq,lb,ub,@twocone,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

disp([output3.funcCount,output3.iterations])

    43     9

辅助函数

以下代码会创建 bigtoleft 辅助函数。

function [f gradf] = bigtoleft(x)
% This is a simple function that grows rapidly negative
% as x(1) becomes negative
%
f = 10*x(:,1).^3+x(:,1).*x(:,2).^2+x(:,3).*(x(:,1).^2+x(:,2).^2);

if nargout > 1

   gradf=[30*x(1)^2+x(2)^2+2*x(3)*x(1);
       2*x(1)*x(2)+2*x(3)*x(2);
       (x(1)^2+x(2)^2)];

end
end

以下代码会创建 twocone 辅助函数。

function [c ceq gradc gradceq] = twocone(x)
% This constraint is two cones, z > -10 + r
% and z < 3 - r

ceq = [];
r = sqrt(x(1)^2 + x(2)^2);
c = [-10+r-x(3);
    x(3)-3+r];

if nargout > 2

    gradceq = [];
    gradc = [x(1)/r,x(1)/r;
       x(2)/r,x(2)/r;
       -1,1];

end
end

以下代码会创建 hessinterior 辅助函数。

function h = hessinterior(x,lambda)

h = [60*x(1)+2*x(3),2*x(2),2*x(1);
    2*x(2),2*(x(1)+x(3)),2*x(2);
    2*x(1),2*x(2),0];% Hessian of f
r = sqrt(x(1)^2+x(2)^2);% radius
rinv3 = 1/r^3;
hessc = [(x(2))^2*rinv3,-x(1)*x(2)*rinv3,0;
    -x(1)*x(2)*rinv3,x(1)^2*rinv3,0;
    0,0,0];% Hessian of both c(1) and c(2)
h = h + lambda.ineqnonlin(1)*hessc + lambda.ineqnonlin(2)*hessc;
end

使用解析黑塞函数的 fmincon 内点算法