使用梯度和 Hessian 稀疏模式进行最小化

此示例说明如何使用稀疏有限差分近似的三对角 Hessian 矩阵（而不是显式计算）来求解非线性最小化问题。

问题可以表示为找出使以下方程最小化的 $x$ ：

$f (x) = \sum_{i = 1}^{n - 1} ({(x_{i}^{2})}^{(x_{i + 1}^{2} + 1)} + {(x_{i + 1}^{2})}^{(x_{i}^{2} + 1)}),$

其中 $n$ = 1000。

n = 1000;

要在 trust-region 中使用 fminunc 方法，您必须计算目标函数中的梯度；它不像在 quasi-newton 方法中那样是可选的。

本示例末尾的辅助函数 brownfg 计算目标函数和梯度。

为了高效计算 Hessian 矩阵 $H (x)$ 的稀疏有限差分近似，必须预先确定 $H$ 的稀疏结构。在这种情况下，稀疏矩阵结构 Hstr 可在文件 brownhstr.mat 中使用。使用 spy 命令，您可以看到 Hstr 确实是稀疏的（只有 2998 个非零）。

load brownhstr
spy(Hstr)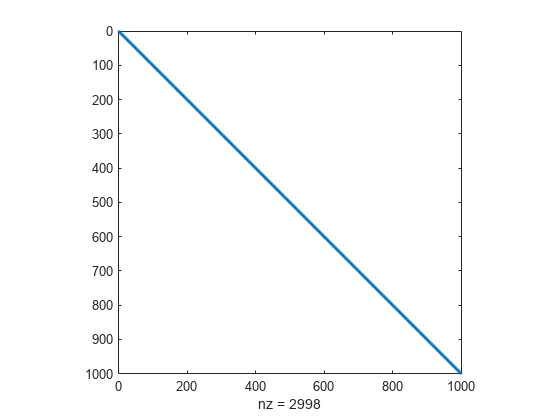

Figure contains an axes object. The axes object with xlabel nz = 2998 contains a line object which displays its values using only markers.

使用 optimoptions 将 HessPattern 选项设置为 Hstr。当如此大的问题具有明显的稀疏结构时，不设置 HessPattern 选项会不必要地使用大量内存和计算，因为 fminunc 尝试对一百万个非零条目的完整 Hessian 矩阵使用有限差分。

要使用 Hessian 稀疏模式，您必须使用 trust-region 的 fminunc 算法。该算法还要求您使用 SpecifyObjectiveGradient 将 true 选项设置为 optimoptions。

options = optimoptions(@fminunc,'Algorithm','trust-region',...
    'SpecifyObjectiveGradient',true,'HessPattern',Hstr);

将目标函数设置为 @brownfg。对于奇数 $x$ 分量，将初始点设置为 -1；对于偶数 $x$ 分量，将初始点设置为 +1。

xstart = -ones(n,1); 
xstart(2:2:n,1) = 1;
fun = @brownfg;

通过使用初始点 fminunc 和选项 xstart 调用 options 来求解问题。

[x,fval,exitflag,output] = fminunc(fun,xstart,options);

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>

检查解和求解过程。

disp(fval)

   7.4738e-17

disp(exitflag)

disp(output)

         iterations: 7
          funcCount: 8
           stepsize: 0.0046
       cgiterations: 7
      firstorderopt: 7.9822e-10
          algorithm: 'trust-region'
            message: 'Local minimum found.↵↵Optimization completed because the size of the gradient is less than↵the value of the optimality tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The first-order optimality measure, 7.982187e-10, ↵is less than options.OptimalityTolerance = 1.000000e-06, and no negative/zero↵curvature is detected in the trust-region model.'
    constrviolation: []

函数 $f (x)$ 是平方幂的和，因此是非负的。解 fval 几乎为零，显然是最小值。退出标志 1 也表示 fminunc 已求得解。output 结构体表明 fminunc 只需 7 次迭代就找到了解。

显示该解的最大和最小元素。

disp(max(x))

   1.9955e-10

disp(min(x))

  -1.9955e-10

该解接近 x = 0 所有元素的点。

辅助函数

以下代码会创建 brownfg 辅助函数。

function [f,g] = brownfg(x)
% BROWNFG Nonlinear minimization test problem
% 
% Evaluate the function
n=length(x); y=zeros(n,1);
i=1:(n-1);
y(i)=(x(i).^2).^(x(i+1).^2+1) + ...
        (x(i+1).^2).^(x(i).^2+1);
  f=sum(y);
% Evaluate the gradient if nargout > 1
  if nargout > 1
     i=1:(n-1); g = zeros(n,1);
     g(i) = 2*(x(i+1).^2+1).*x(i).* ...
              ((x(i).^2).^(x(i+1).^2))+ ...
              2*x(i).*((x(i+1).^2).^(x(i).^2+1)).* ...
              log(x(i+1).^2);
     g(i+1) = g(i+1) + ...
              2*x(i+1).*((x(i).^2).^(x(i+1).^2+1)).* ...
              log(x(i).^2) + ...
              2*(x(i).^2+1).*x(i+1).* ...
              ((x(i+1).^2).^(x(i).^2));
  end
end

另请参阅

主题

使用梯度和黑塞矩阵的最小化