多目标达成优化

此示例说明如何使用多目标实现方法求解极点配置问题。该算法在函数 fgoalattain 中实现。

描述系统演化的方程

考虑一个 2 输入 2 输出的不稳定工厂。描述系统 $x (t)$ 演化的方程是

$\frac{d x}{d t} = A x (t) + B u (t),$

其中 $u (t)$ 是输入（控制）信号。系统的输出是

$y (t) = C x (t) .$

矩阵 $A$ 、 $B$ 和 $C$ 是

A =  [ -0.5  0  0;  0  -2  10;  0  1  -2 ];
B =  [ 1  0;  -2  2;  0  1 ];
C =  [ 1  0  0;  0  0  1 ];

优化目标

假设控制信号 $u (t)$ 设置为与输出 $y (t)$ 成比例：

$u (t) = K y (t)$

对于某个矩阵 $K$ 。

这意味着系统 $x (t)$ 的演变是：

$\frac{d x}{d t} = A x (t) + B K C x (t) = (A + B K C) x (t) .$

优化的目标是设计 $K$ 具有以下两个属性：

1. $(A + B K C)$ 的特征值的实部小于 [-5, -3, -1]。（在控制文献中这被称为极点配置。）

2. abs( $K$ ) <= 4（ $K$ 的每个元素都在 -4 和 4 之间）

为了求解优化问题，首先设定多目标目标：

goal = [-5, -3, -1];

将权重设置为与目标相等，以确保目标的未完成或超额完成百分比相同。

weight = abs(goal);

初始化输出反馈控制器

K0 = [ -1 -1; -1 -1];

设置控制器的上界和下界

lb = repmat(-4,size(K0))

lb = 2×2

    -4    -4
    -4    -4

ub = repmat(4,size(K0))

设置优化显示参数以在每次迭代时给出输出：

options = optimoptions('fgoalattain','Display','iter');

创建一个向量值函数 eigfun，返回闭环系统的特征值。此函数需要额外的参数（即矩阵 $A$ 、 $B$ 和 $C$ ）；传递这些参数最方便的方式是通过匿名函数：

eigfun = @(K) sort(eig(A+B*K*C));

调用优化解

为了开始优化，我们调用 fgoalattain：

[K,~,attainfactor] = ...
        fgoalattain(eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options);

                 Attainment        Max     Line search     Directional 
 Iter F-count        factor    constraint   steplength      derivative   Procedure 
    0      6              0       1.88521                                            
    1     13          1.031       0.02998            1           0.745     
    2     20         0.3525       0.06863            1          -0.613     
    3     27        -0.1706        0.1071            1          -0.223    Hessian modified  
    4     34        -0.2236       0.06654            1          -0.234    Hessian modified twice  
    5     41        -0.3568      0.007894            1         -0.0812     
    6     48        -0.3645      0.000145            1          -0.164    Hessian modified  
    7     55        -0.3645             0            1        -0.00515    Hessian modified  
    8     62        -0.3675     0.0001548            1        -0.00812    Hessian modified twice  
    9     69        -0.3889      0.008327            1        -0.00751    Hessian modified  
   10     76        -0.3862             0            1         0.00568     
   11     83        -0.3863     4.469e-13            1          -0.998    Hessian modified twice  

Local minimum possible. Constraints satisfied.

fgoalattain stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

解的控制参数值为：

K = 2×2

   -4.0000   -0.2564
   -4.0000   -4.0000

闭环系统的特征值在 eigfun(K) 中如下：（它们也保存在输出 fval 中）

eigfun(K)

ans = 3×1

   -6.9313
   -4.1588
   -1.4099

成就因素表明目标实现的水平。负的成就因子表示成绩超额，正的成就因子表示成绩不佳。我们在这次运行中获得的价值实现因子表明，目标已经超额完成近 40％：

attainfactor

attainfactor = -0.3863

通过 ODE 解进行系统演化

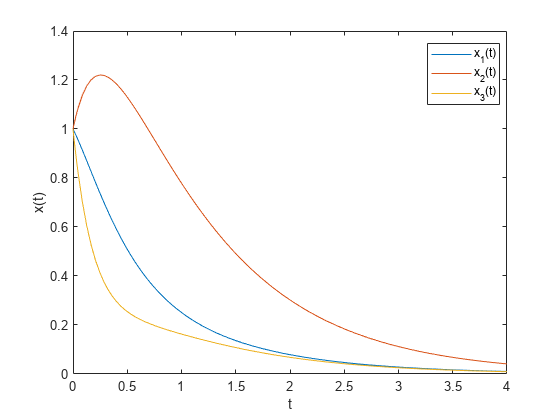
以下是系统 $x (t)$ 从时间 0 到时间 4 的演变过程，使用计算出的反馈矩阵 $K$ ，从点 x(0) = [1;1;1] 开始。

首先解微分方程：

[Times, xvals] = ode45(@(u,x)((A + B*K*C)*x),[0,4],[1;1;1]);

然后绘制结果：

plot(Times,xvals)
legend('x_1(t)','x_2(t)','x_3(t)','Location','best')
xlabel('t');
ylabel('x(t)');

设定要实现的目标

假设我们现在要求特征值尽可能接近目标值[-5，-3，-1]。将 options.EqualityGoalCount 设置为应尽可能接近目标的目标数量（即，不要试图过度实现）：

所有三个目标都应尽可能接近目标。

options.EqualityGoalCount = 3;

调用优化解

我们准备调用优化求解器：

[K,fval,attainfactor,exitflag,output,lambda] = ...
    fgoalattain(eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options);

                 Attainment        Max     Line search     Directional 
 Iter F-count        factor    constraint   steplength      derivative   Procedure 
    0      6              0       1.88521                                            
    1     13          1.031       0.02998            1           0.745     
    2     20         0.3525       0.06863            1          -0.613     
    3     27         0.1528     -0.009105            1           -0.22    Hessian modified  
    4     34        0.02684       0.03722            1          -0.166    Hessian modified  
    5     41      1.041e-17      0.005702            1          -0.116    Hessian modified  
    6     48      1.459e-18     9.699e-06            1       -7.73e-16    Hessian modified  
    7     55     -5.082e-23     4.969e-11            1       -7.65e-14    Hessian modified  

Local minimum possible. Constraints satisfied.

fgoalattain stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

该解的控制参数值为：

K = 2×2

   -1.5954    1.2040
   -0.4201   -2.9046

这次闭环系统的特征值也保存在输出 fval 中，如下所示：

eigfun(K)

ans = 3×1

   -5.0000
   -3.0000
   -1.0000

成就因素是目标实现的水平。负的成就因子表示成绩超额，正的成就因子表示成绩不佳。获得的低达到因子表明特征值几乎完全满足目标：

attainfactor

attainfactor = -5.0824e-23

通过求解 ODE 观察系统演变

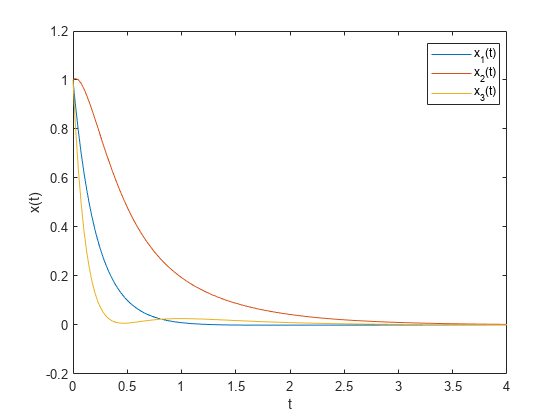
以下是系统 $x (t)$ 从时间 0 到时间 4 的演变过程，使用新计算的反馈矩阵 $K$ ，从点 x(0) = [1;1;1] 开始。

首先解微分方程：

[Times, xvals] = ode45(@(u,x)((A + B*K*C)*x),[0,4],[1;1;1]);

然后绘制结果：

plot(Times,xvals)
legend('x_1(t)','x_2(t)','x_3(t)','Location','best')
xlabel('t');
ylabel('x(t)');

另请参阅

fgoalattain

多目标达成优化

描述系统演化的方程

优化目标

调用优化解

通过 ODE 解进行系统演化

设定要实现的目标

调用优化解

通过求解 ODE 观察系统演变

另请参阅

相关主题

WeChat