或者而不是和约束

本页采用了机器翻译。点击此处可查看最新英文版本。

一般来说，求解器采用隐式 AND 约束：

约束 1 AND 约束 2 AND 约束 3 全部满足。

但是，有时您需要一个 OR：

约束 1 或约束 2 或约束 3 得到满足。

这些表示在逻辑上并不等价，并且通常没有办法用 AND 约束来表达 OR 约束。

提示

幸运的是，非线性约束极其灵活。只需将非线性约束函数设置为约束函数的最小值，即可获得 OR 约束。

您可以将最小值设置为约束的原因是由于非线性约束的性质：您将它们作为一组在可行点必须为负的函数。如果您的约束为

F₁(x) ≤ 0 或 F₂(x) ≤ 0 或 F₃(x) ≤ 0,

然后将非线性不等式约束函数 c（x）设置为：

c(x) = min(F₁(x),F₂(x),F₃(x))。

由于最小值，c(x) 并不平滑，这是对约束函数的一般要求。尽管如此，该方法通常有效。

注意

您不能在 OR 约束中使用通常的边界和线性约束。相反，将边界和线性约束转换为非线性约束函数，如本例所示。

例如，假设可行区域是 L 形区域：x 位于矩形 –1 ≤ x(1) ≤ 1, 0 ≤ x(2) ≤ 1 内，或者 x 位于矩形 0 ≤ x(1) ≤ 1, –1 ≤ x(2) ≤ 1 内。

用于创建图窗的代码

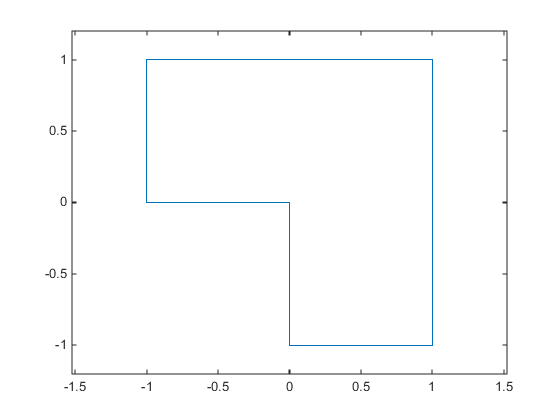
为了将矩形表示为非线性约束，而不是边界约束，构造一个在矩形内为负的函数 a ≤ x(1) ≤ b, c ≤ x(2) ≤ d：

function cout = rectconstr(x,a,b,c,d)
% Negative when  x is in the rectangle [a,b][c,d]
% First check that a,b,c,d are in the correct order

if (b <= a) || (d <= c)
    error('Give a rectangle a < b, c < d')
end

cout = max([(x(1)-b),(x(2)-d),(a-x(1)),(c-x(2))]);

按照使用非线性约束函数最小值的规定，对于 L 形区域，非线性约束函数为：

function [c,ceq] = rectconstrfcn(x)

ceq = []; % no equality constraint
F(1) = rectconstr(x,-1,1,0,1); % one rectangle
F(2) = rectconstr(x,0,1,-1,1); % another rectangle
c = min(F); % for OR constraints

用于创建图窗的代码

假设您的目标函数是

fun = @(x)exp(x(1)) * (4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) + 2*x(2) + 1);

在 L 形区域内最小化 fun：

opts = optimoptions(@fmincon,'Algorithm','interior-point','Display','off');
x0 = [-.5,.6]; % an arbitrary guess
[xsol,fval,eflag] = fmincon(fun,x0,[],[],[],[],[],[],@rectconstrfcn,opts)

xsol =

    0.4998   -0.9996


fval =

   2.4650e-07


eflag =

     1

显然，解 xsol 位于 L 形区域内。退出标志为 1，表示 xsol 是局部最小值。

另请参阅

fmincon

主题

非线性约束