使用半无限规划分析不确定性的影响

最小堆叠高度问题

考虑一个 20 公里×20 公里的区域 R，其中要放置十个烟囱。这些烟囱向大气中排放多种污染物，其中之一就是二氧化硫。堆栈的 x、y 位置是固定的，但堆栈的高度可以变化。

烟囱的建造者希望尽量降低烟囱的总高度，从而尽量降低建设成本。然而，这与相互矛盾的要求相平衡，即 R 区域地面任何一点的二氧化硫浓度不得超过法定的最高限值。

首先，让我们绘制烟囱的初始高度。请注意，我们放大了 R 中包含烟囱的 4 公里×4 公里的子区域。

h0 = [210;210;180;180;150;150;120;120;90;90];
plotChimneyStacks(h0, 'Chimney Stack Initial Height');

这个问题有两个与环境相关的参数，风速和风向。在这个示例的后面我们将允许这些参数变化，但是对于第一个问题我们将这些参数设置为典型值。

% Wind direction in radians
theta0 = 3.996;   
% Wind speed in m/s
U0 = 5.64;

现在让我们绘制整个区域 R 内二氧化硫 (SO2) 的地面浓度图（请记住烟囱图位于较小的区域内）。已根据烟囱的初始高度计算了 SO2 浓度。

我们可以看到 SO2 的浓度在感兴趣的区域内变化。二氧化硫图表有两个值得注意的特点：

简单来说，第一个特征是由于盛行风造成的，在这个示例中，盛行风将 SO2 吹向 (x,y) 平面的左上角。第二个因素是由于 SO2 通过扩散输送到地面。与盛行风相比，这是一个较慢的过程，因此 SO2 仅到达感兴趣区域左上角的地面。

有关烟囱大气扩散的更详细讨论，请参阅介绍中引用的参考资料。

粉色平面表示 SO2 浓度为 $0.000125g{m}^{-3}$。这是 R 区域内二氧化硫浓度不得超过的法定最大值。从图中可以清楚地看到，SO2 浓度超过了烟囱初始高度的最大值。

检查 MATLAB 文件 concSulfurDioxide，了解二氧化硫浓度是如何计算的。

plotSulfurDioxide(h0, theta0, U0, ...
    'Sulfur Dioxide Concentration at Initial Stack Height');

fseminf 的工作原理

在我们求解最小堆栈高度问题之前，我们将概述 fseminf 如何求解半无限问题。一般半无限规划问题可以表述为：

使得

$Ax<=b$（线性不等式约束）

$Aeq*x=beq$（线性等式约束）

$c(x)<=0$（非线性不等式约束）

$ceq(x)=0$（非线性等式约束）

$l<=x<=u$（边界）

和

$K_j(x,w)<=0$，其中 $w\in I_j$ 为 $j=1,...,n_{inf}$ （非线性半无限约束）

该算法允许您为非线性优化问题指定约束，该约束必须在辅助变量 $w$ 的区间内满足。请注意，对于 fseminf，对于每个半无限约束，此变量被限制为 1 维或 2 维。

函数 fseminf 从初始值 $x_0$ 开始，使用迭代过程来获得最优解 $x_{opt}$ ，从而求解一般半无限问题。

该算法的关键分量是处理“半无限”约束，$K_j$。在 $x_{opt}$ 处，要求 $K_j$ 在区间 $I_j$ 内的每个 $w$ 值处必须是可行的。通过考虑区间 $I_j$ 内 $K_j$ 相对于 $w$ 的所有局部极大值，可以简化这一约束。原始约束相当于要求上述每个局部极大值处的 $K_j$ 的值都是可行的。

fseminf 计算每个半无限约束的所有局部最大值的近似值 $K_j$。为此，fseminf 首先计算 $w$ 值网格上的每个半无限约束。然后使用一个简单的差分方案从评估的半无限约束中计算 $K_j$ 的所有局部最大值。

正如我们稍后将看到的，您可以在约束函数中创建这个网格。网格每个 $w$ 坐标应使用的间距由 fseminf 提供给约束函数。

在算法的每次迭代中，执行以下步骤：

编写非线性约束函数

在调用 fseminf 来求解问题之前，我们需要编写一个函数来评估该问题中的非线性约束。要实施的约束是，区域 R 中的每个点的地面二氧化硫浓度不得超过 $0.000125g{m}^{-3}$。

这是一个半无限约束，本节讲解了约束函数的实现。对于最小堆栈高度问题，我们已经在 MATLAB 文件 airPollutionCon 中实现了约束。

type airPollutionCon.m

function [c, ceq, K, s] = airPollutionCon(h, s, theta, U)
%AIRPOLLUTIONCON Constraint function for air pollution demo
% 
%   [C, CEQ, K, S] = AIRPOLLUTIONCON(H, S, THETA, U) calculates the
%   constraints for the air pollution Optimization Toolbox (TM) demo. This
%   function first creates a grid of (X, Y) points using the supplied grid
%   spacing, S. The following constraint is then calculated over each point
%   of the grid:
%
%   Sulfur Dioxide concentration at the specified wind direction, THETA and
%   wind speed U <= 1.25e-4 g/m^3
%
%   See also AIRPOLLUTION

%   Copyright 2008 The MathWorks, Inc.

% Initial sampling interval
if nargin < 2 || isnan(s(1,1))
    s = [1000 4000]; 
end

% Define the grid that the "infinite" constraints will be evaluated over
w1x = -20000:s(1,1):20000;
w1y = -20000:s(1,2):20000;
[t1,t2] = meshgrid(w1x,w1y);

% Maximum allowed sulphur dioxide
maxsul = 1.25e-4; 

% Calculate the constraint over the grid
K = concSulfurDioxide(t1, t2, h, theta, U) - maxsul;

% Rescale constraint to make it 0(1)
K = 1e4*K;

% No finite constraints
c = [];
ceq = [];

该函数说明了半无限规划问题的约束函数的一般结构。具体来说，fseminf 的约束函数可以分为三个部分：

1.定义约束评估的初始网格尺寸

回想一下，fseminf 将网格上的“半无限”约束作为这些约束的整体计算的一部分进行评估。当您的约束函数被 fseminf 调用时，您应该使用的网格间距将提供给您的函数。Fseminf 将首先调用您的约束函数，并将网格间距 s 设置为 NaN。这使您可以初始化约束评估的网格大小。这里，我们在两个“无限”变量中有一个“无限”约束。这意味着我们需要将网格大小初始化为 1×2 矩阵，在本例中为 s = [1000 4000]。

2.定义用于约束评估的网格

需要创建用于约束评估的网格。airPollutionCon 中注释“定义将评估“无限”约束的网格”后面的三行代码可以针对大多数二维半无限规划问题进行修改。

3.计算网格上的约束

一旦定义了网格，就可以计算其约束。然后将这些约束从上面的约束函数返回给 fseminf。

请注意，在这个问题中，我们还重新调整了约束，以便它们在更接近目标函数的尺度上变化。这有助于 fseminf 避免与在不同规模上变化的目标和约束相关的缩放问题。

求解优化问题

我们现在可以调用 fseminf 来求解问题。所有烟囱的高度必须至少为 10 米，我们使用之前指定的初始烟囱高度。请注意，下面 (1) 的 fseminf 的第三个输入参量表示只有一个半无限约束。

lb = 10*ones(size(h0));
[hsopt, sumh, exitflag] = fseminf(@(h)sum(h), h0, 1, ...
    @(h,s) airPollutionCon(h,s,theta0,U0), [], [], [], [], lb);

Local minimum possible. Constraints satisfied.

fseminf stopped because the predicted change in the objective function
is less than the value of the function tolerance and constraints 
are satisfied to within the value of the constraint tolerance.

fprintf('\nMinimum computed cumulative height of chimney stacks : %7.2f m\n', sumh);

Minimum computed cumulative height of chimney stacks : 3667.19 m

fseminf 计算出的最小累积高度远高于烟囱的初始总高度。我们将在示例后面的部分看到当问题中添加参数不确定性时最小累积高度如何变化。现在，让我们绘制烟囱的最佳高度。

检查 MATLAB 文件 plotChimneyStacks 以了解图表是如何生成的。

plotChimneyStacks(hsopt, 'Chimney Stack Optimal Height');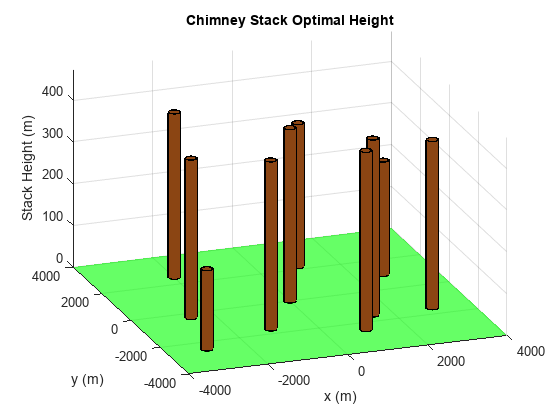

检查优化结果

回想一下，fseminf 通过确保约束的离散极大值低于指定的边界来确定半无限约束在任何地方都得到满足。通过绘制地面二氧化硫浓度与最佳烟囱高度的关系，我们能够验证半无限约束在任何地方都得到满足。

请注意，二氧化硫浓度在 (x, y) 平面的左上角达到最大值，即在 x = -20000m，y = 20000m 处。该点在下图中以蓝点标记，并通过计算该点的二氧化硫浓度进行验证。

检查 MATLAB 文件 plotSulfurDioxide 以了解图表是如何生成的。

titleStr = 'Optimal Sulfur Dioxide Concentration and its maximum (blue)';
xMaxSD = [-20000 20000];
plotSulfurDioxide(hsopt, theta0, U0, titleStr, xMaxSD);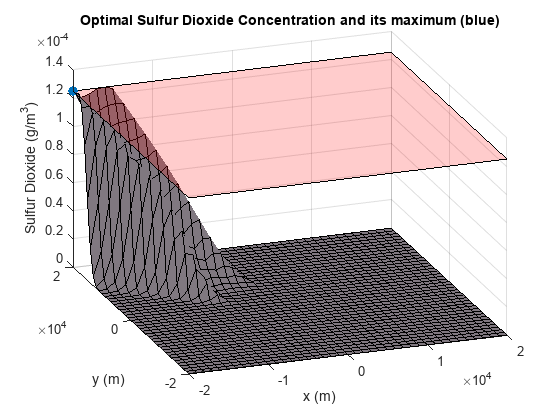

SO2Max = concSulfurDioxide(-20000, 20000, hsopt, theta0, U0);
fprintf('Sulfur Dioxide Concentration at x = -20000m, y = 20000m : %e g/m^3\n', SO2Max);

Sulfur Dioxide Concentration at x = -20000m, y = 20000m : 1.250000e-04 g/m^3

考虑环境因素的不确定性

二氧化硫浓度取决于几个环境因素，这些因素在上述问题中保持为固定值。两个环境因素是风速和风向。有关所有问题参数的更详细讨论，请参阅介绍中引用的参考资料。

我们可以研究系统随着风速和风向的变化。在本例的这一部分，我们要确保即使风向从 3.82 弧度变为 4.18 弧度并且平均风速在 5 到 6.2 米/秒之间变化，也能满足二氧化硫限值。

我们需要实施半无限约束来确保二氧化硫浓度不超过区域 R 内的限值。要求此约束对于所有风速和风向对都是可行的。

这样的约束将有四个“无限”变量（风速和风向以及地面的 xy 坐标）。但是，提供给 fseminf 的任何半无限约束最多只能有两个“无限”变量。

为了以适合 fseminf 的形式实现这一约束，我们回想一下上一个问题中最优烟囱高度处的 SO2 浓度。具体来说，SO2 浓度在 x = -20000m，y = 20000m 处取得最大值。为了减少“无限”变量的数量，我们假设当存在不确定性时，SO2 浓度也将在此时取其最大值。然后，我们要求此时的 SO2 浓度在所有风速和风向对中都低于 $0.000125g{m}^{-3}$

这意味着这个问题的“无限”变量是风速和风向。要了解如何实施此约束，请检查 MATLAB 文件 uncertainAirPollutionCon。

type uncertainAirPollutionCon.m

function [c, ceq, K, s] = uncertainAirPollutionCon(h, s)
%UNCERTAINAIRPOLLUTIONCON Constraint function for air pollution demo
% 
%   [C, CEQ, K, S] = UNCERTAINAIRPOLLUTIONCON(H, S) calculates the
%   constraints for the fseminf Optimization Toolbox (TM) demo. This
%   function first creates a grid of wind speed/direction points using the
%   supplied grid spacing, S. The following constraint is then calculated
%   over each point of the grid:
%
%   Sulfur Dioxide concentration at x = -20000m, y = 20000m <= 1.25e-4
%   g/m^3
%
%   See also AIRPOLLUTIONCON, AIRPOLLUTION

%   Copyright 2008 The MathWorks, Inc.

% Maximum allowed sulphur dioxide
maxsul = 1.25e-4; 

% Initial sampling interval
if nargin < 2 || isnan(s(1,1))
    s = [0.02 0.04]; 
end

% Define the grid that the "infinite" constraints will be evaluated over
w1x = 3.82:s(1,1):4.18; % Wind direction
w1y = 5.0:s(1,2):6.2;   % Wind speed
[t1,t2] = meshgrid(w1x,w1y);

% We assume the maximum SO2 concentration is at [x, y] = [-20000, 20000]
% for all wind speed/direction pairs. We evaluate the SO2 constraint over
% the [theta, U] grid at this point.
K = concSulfurDioxide(-20000, 20000, h, t1, t2) - maxsul;
 
% Rescale constraint to make it 0(1)
K = 1e4*K;

% No finite constraints
c = [];
ceq = [];

该约束函数可以分为与之前相同的三个部分：

1.定义约束评估的初始网格尺寸

注释“初始采样间隔”后面的代码初始化网格大小。

2.定义用于约束评估的网格

下一部分代码使用与初始问题中类似的构造创建一个网格（现在是风速和风向）。

3.计算网格上的约束

代码的其余部分计算风速/风向网格每个点的 SO2 浓度。然后将这些约束从上面的约束函数返回给 fseminf。

现在我们可以调用 fseminf 来求解考虑环境因素的不确定性的堆栈高度问题。

[hsopt2, sumh2, exitflag2] = fseminf(@(h)sum(h), h0, 1, ...
    @uncertainAirPollutionCon, [], [], [], [], lb);

Local minimum possible. Constraints satisfied.

fseminf stopped because the predicted change in the objective function
is less than the value of the function tolerance and constraints 
are satisfied to within the value of the constraint tolerance.

fprintf('\nMinimal computed cumulative height of chimney stacks with uncertainty: %7.2f m\n', sumh2);

Minimal computed cumulative height of chimney stacks with uncertainty: 3812.01 m

现在我们可以看看有和没有参数不确定性的问题的最小计算累积堆栈高度之间的差异。您应该能够看到，当问题中添加不确定性时，最小累积高度会增加。预期的高度增加使 SO2 浓度在指定范围内的所有风速/风向对中保持低于法定最高值。

我们可以通过检查二氧化硫图来确认二氧化硫浓度不超过感兴趣区域的限值。对于给定的 (x, y) 点，我们绘制了规定范围内风速和风向的最大 SO2 浓度。请注意，我们放大了 X-Y 平面的左上角。

titleStr = 'Optimal Sulfur Dioxide Concentration under Uncertainty';
thetaRange = 3.82:0.02:4.18;
URange = 5:0.2:6.2;
XRange = [-20000,-15000];
YRange = [15000,20000];
plotSulfurDioxideUncertain(hsopt2, thetaRange, URange, XRange, YRange, titleStr);

当问题定义不确定时，我们最终绘制烟囱的最佳高度。

plotChimneyStacks(hsopt2, 'Chimney Stack Optimal Height under Uncertainty');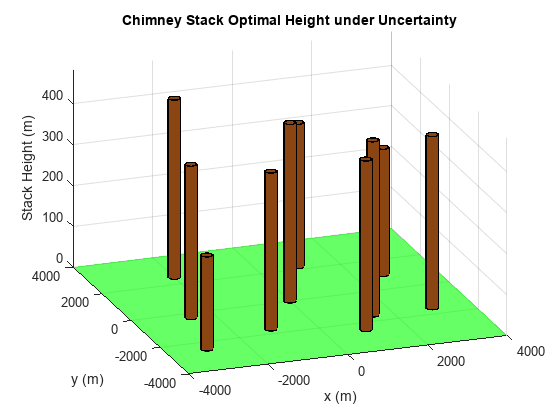

半无限规划算法 fseminf 有很多可用的选项。有关详细信息，请参阅《Optimization Toolbox™ 用户指南》，其中的“使用 Optimization Toolbox 求解器”一章中的“约束非线性优化：fseminf 问题表示和算法”。