Main Content

二维半无限约束

找到最小化 x 的值

f(x) = (x1 – 0.2)2 + (x2– 0.2)2 + (x3– 0.2)2,

其中

K1(x,w)=sin(w1x1)cos(w2x2)−11000(w1−50)2−sin(w1x3)−x3+...                 sin(w2x2)cos(w1x1)−11000(w2−50)2−sin(w2x3)−x3≤1.5,

对于范围内的所有 w1 和 w2 值

1 ≤ w1 ≤ 100,
1 ≤ w2 ≤ 100,

初始点为 x = [0.25,0.25,0.25]。

注意半无限约束是二维的，即矩阵。

首先，编写一个计算目标函数的文件。

function f = myfun(x,s)
% Objective function
f = sum((x-0.2).^2);

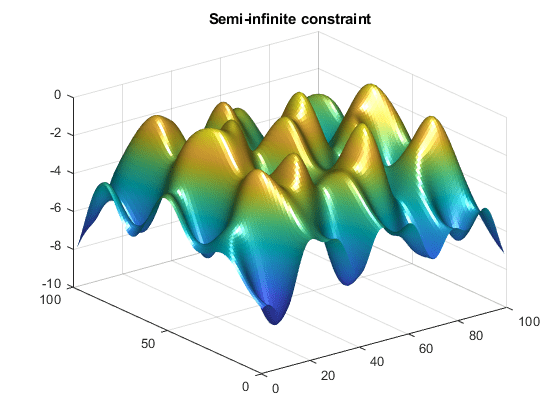
其次，为约束编写一个文件，名为 mycon.m。每次调用 mycon 时，包含绘制半无限约束的表面图的代码。这样您就可以看到在最小化 X 时约束如何变化。

function [c,ceq,K1,s] = mycon(X,s)
% Initial sampling interval
if isnan(s(1,1)),
   s = [2 2];
end

% Sampling set
w1x = 1:s(1,1):100;
w1y = 1:s(1,2):100;
[wx,wy] = meshgrid(w1x,w1y);

% Semi-infinite constraint 
K1 = sin(wx*X(1)).*cos(wx*X(2))-1/1000*(wx-50).^2 -...
       sin(wx*X(3))-X(3)+sin(wy*X(2)).*cos(wx*X(1))-...
       1/1000*(wy-50).^2-sin(wy*X(3))-X(3)-1.5;

% No finite nonlinear constraints
c = []; ceq=[];

% Mesh plot
m = surf(wx,wy,K1,'edgecolor','none','facecolor','interp');
camlight headlight
title('Semi-infinite constraint')
drawnow

接下来，调用优化程序。

x0 = [0.25, 0.25, 0.25];    % Starting guess
[x,fval] = fseminf(@myfun,x0,1,@mycon)

经过九次迭代后，解是

x
x =
    0.2523    0.1715    0.1938

解处的函数值为

fval
fval =
    0.0036

目标是最小化目标 f(x)，使得半无限约束满足 K1(x,w) ≤ 1.5。在解 x 处评估 mycon 并查看矩阵 K1 的最大元素表明该约束很容易满足。

[c,ceq,K1] = mycon(x,[0.5,0.5]);  % Sampling interval 0.5
max(max(K1))
ans =
   -0.0370

对 mycon 的调用产生了以下冲浪图，该图显示了 x 处的半无限约束。

Wavy surface less than or equal to zero, with some points attaining zero

另请参阅

相关主题