本页采用了机器翻译。点击此处可查看最新英文版本。

非光滑函数的光滑表示

为了求解原本不顺利的问题，有时可以添加辅助变量。例如，

f(x) = max(g(x),h(x))

即使 g(x) 和 h(x) 是平滑函数，也可能是非平滑函数，如以下函数所示。

g(x)=sin(x)h(x)=cos(x)f(x)=max(g(x),h(x)).

f(x) 在点 x = π/4 和 x = 5π/4 处是非平滑的。

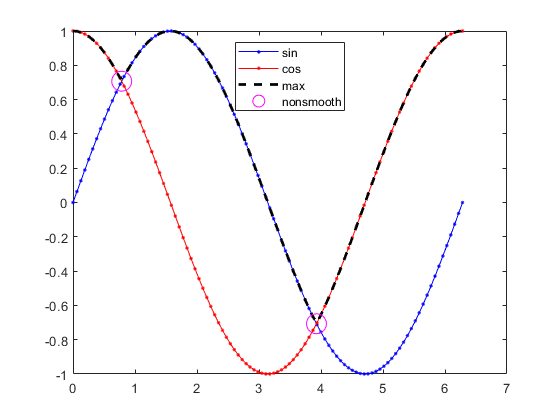
Max of sine and cosine is nonsmooth at x = pi/4, x = 5*pi/4

 用于创建图窗的代码

这种缺乏平滑度的情况会给 Optimization Toolbox™ 求解器带来问题，所有求解器都假设目标函数和非线性约束函数是连续可微的。所以，如果您尝试求解

x = mint(f(t)) 从点 x0 = 1 开始，

您不会获得退出标志 1，因为该解在局部最小点 x = π/4 处不可微。

fun1 = @sin;
fun2 = @cos;
fun = @(x)max(fun1(x),fun2(x));
[x1,fval1,eflag1] = fminunc(fun,1)
Local minimum possible.

fminunc stopped because it cannot decrease the objective function
along the current search direction.

<stopping criteria details>

x1 =

    0.7854


fval1 =

    0.7071


eflag1 =

     5

有时，您可以使用辅助变量将非光滑问题转变为光滑问题。对于前面的示例，考虑具有平滑约束的辅助变量 y

y≥g(x)y≥h(x).

考虑优化问题，受这些约束的影响，

minxy.

得到的解 x, y 就是原问题的解

minxf(x)=minxmax(g(x),h(x)).

这个表示采用基于问题的方法。

myvar = optimvar("myvar");
auxvar = optimvar("auxvar");
smprob = optimproblem("Objective",auxvar);
smprob.Constraints.cons1 = auxvar >= sin(myvar);
smprob.Constraints.cons2 = auxvar >= cos(myvar);
x0.myvar = 1;
x0.auxvar = 1;
[sol2,fval2,eflag2] = solve(smprob,x0)
Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

sol2 = 

  struct with fields:

    auxvar: 0.7071
     myvar: 0.7854


fval2 =

    0.7071


eflag2 = 

    OptimalSolution

fminimax 函数的表示也基于此概念；请参阅 目标达成方法。

另请参阅

|

主题