本页采用了机器翻译。点击此处可查看最新英文版本。

使用分布式数组通过直接方法求解线性方程组

打开实时脚本

此示例显示如何使用分布式数组的直接方法并行求解形式为 Ax=b 的线性方程组。

分布式数组非常适合大型数学计算，例如线性代数的大型问题。与存储在客户端内存中的数组相同，您可以使用 mldivide 来解决使用分布式数组定义的线性方程组，因此您无需更改代码。

分布式数组将数据从客户端工作区分发到本地计算机或集群中的并行池。每个工作单元将数组的一部分存储在其内存中，但也可以与其他工作单元通信以访问数组的所有段。分布式数组可以包含不同类型的数据，包括完整矩阵和稀疏矩阵。

求解线性方程的直接方法通常对系数矩阵 A 进行分解以计算解。mldivide 根据 A 的结构以及 A 是满的还是稀疏的，从一组直接求解器方法中选择一种。

此示例说明如何求解形式为 Ax=b 的简单线性方程组，并得到精确的已知解 x。该系统由矩阵 A 和列向量 b 定义。解 x 也是一个列向量。在这个示例中，系统使用满矩阵和稀疏矩阵来定义。对于使用分布式数组或客户端内存上的数组定义的系统，所需的代码是相同的。

有关如何使用迭代求解器和分布式数组的相关示例，请参阅 使用分布式数组通过迭代方法求解线性方程组。

解决全矩阵系统

首先将系数矩阵 A 定义为客户端内存中的变量 A，然后将该矩阵传递给 创建函数以创建相同矩阵的分布式版本 ADist。当您使用 distributed 函数时，MATLAB 会使用您的默认集群设置自动启动并行池。

n = 1e3;
A = randi(100,n,n);
ADist = distributed(A);

您现在可以定义右侧向量 b。在这个示例中，b 被定义为 A 的行和，这导致了 Ax=b 形式为 xexact=[1,...,1]T 的精确解。 

b = sum(A,2);
bDist = sum(ADist,2);

由于 sum 作用于分布式数组，因此 bDist 也是分布式的，其数据存储在并行池工作单元的内存中。最后，定义精确解，以便与使用直接数值方法获得的解进行比较。

xEx = ones(n,1);
xDistEx = ones(n,1,'distributed');

现在您已经定义了线性方程组，您可以使用 mldivide 直接求解该系统。在 MATLAB 中，您可以使用特殊运算符 mldivide 调用 \。您不需要更改代码来解决分布式系统，因为 mldivide 自动支持分布式数组。

一旦计算出解决方案，您就可以检查获得的结果 x 的每个元素与 xexact 的预期值之间的误差。

x = A\b;
err = abs(xEx-x);

xDist = ADist\bDist;
errDist = abs(xDistEx-xDist);

figure
subplot(2,1,1)
semilogy(err,'o');
title('System of Linear Equations with Full Matrices');
ylabel('Absolute Error');
xlabel('Element in x');
ylim([10e-17,10e-13])
subplot(2,1,2)
semilogy(errDist,'o');
title('System of Linear Equations with Distributed Full Matrices');
ylabel('Absolute Error');
xlabel('Element in x');
ylim([10e-17,10e-13])

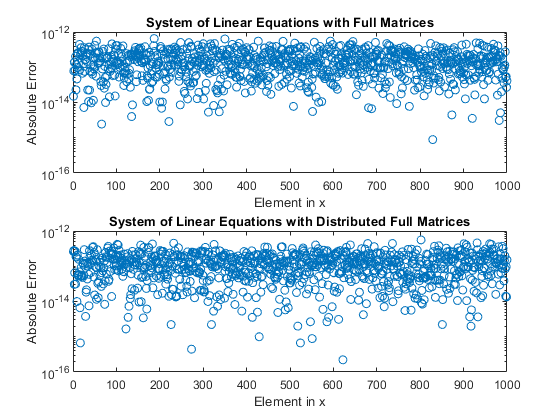
无论是对于分布式数组还是存储在客户端的数组，x 的计算结果和精确结果 xexact 之间的绝对误差都很小。对于两种数组类型来说，解决方案的精度大致相同。

mean(err)
ans = 1.6031e-13

mean(errDist)
ans =

   1.2426e-13

求解稀疏矩阵系统

分布式数组也可以包含稀疏数据。要创建系数矩阵 A，请使用 sprand 和 speye 直接生成随机数的稀疏矩阵加上稀疏单位矩阵。添加单位矩阵有助于防止创建 A 作为奇异矩阵或近奇异矩阵，这两个矩阵都很难分解。 

n = 1e3;
density = 0.2;
A = sprand(n,n,density) + speye(n);
ADist = distributed(A);

选择右侧向量 b 作为 A 的行和，可得到与全矩阵系统的解相同形式的精确解。 

b = sum(A,2);
bDist = sum(ADist,2);
xEx = ones(n,1);
xDistEx = ones(n,1,'distributed');

与全矩阵相同，您现在可以直接使用 mldivide 求解该线性方程组，并检查所得结果与其预期值之间的误差。

x = A\b;
err = abs(xEx-x);

xDist = ADist\bDist;
errDist = abs(xDistEx-xDist);

figure
subplot(2,1,1)
semilogy(err,'o');
title('System of Linear Equations with In-Client Sparse Matrices');
ylabel('Absolute Error');
xlabel('Element in x');
ylim([10e-17,10e-13])
subplot(2,1,2)
semilogy(errDist,'o');
title('System of Linear Equations with Distributed Sparse Matrices');
ylabel('Absolute Error');
xlabel('Element in x');
ylim([10e-17,10e-13])

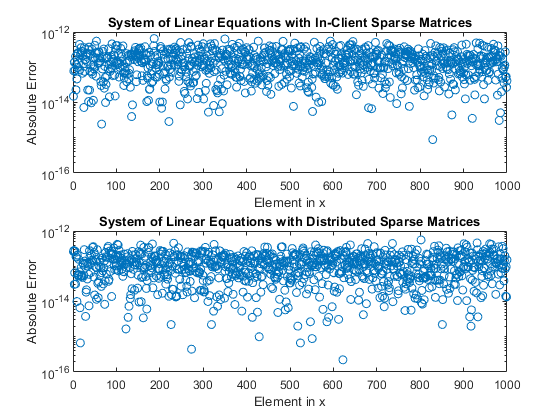
与全矩阵系统一样，使用客户端数组和分布式数组求解线性方程组可以得到具有相当精度的解。

mean(err)
ans = 1.6031e-13

mean(errDist)
ans =

   1.2426e-13

完成计算后，您可以删除并行池。gcp函数返回当前并行池对象，以便您可以删除当前池。

delete(gcp('nocreate'));

提高解决方案的效率

对于某些类型的大型稀疏系数矩阵 A，有比直接分解更有效的方法来解决您的系统。在这些情况下，迭代方法可能更有效地解决线性方程组。迭代方法生成一系列近似解，并收敛到最终结果。有关如何使用迭代方法求解具有大型稀疏输入矩阵的线性方程的示例，请参阅 使用分布式数组通过迭代方法求解线性方程组。

另请参阅

| |

主题