Main Content

interpolateHarmonicField

Interpolate electric or magnetic field in harmonic result at arbitrary spatial locations

Since R2022a

collapse all in page

Syntax

EHintrp = interpolateHarmonicField(harmonicresults,xq,yq)
EHintrp = interpolateHarmonicField(harmonicresults,xq,yq,zq)
EHintrp = interpolateHarmonicField(harmonicresults,querypoints)

Description

EHintrp = interpolateHarmonicField(harmonicresults,xq,yq) returns the interpolated electric or magnetic field values at the 2-D points specified in xq and yq.

example

EHintrp = interpolateHarmonicField(harmonicresults,xq,yq,zq) uses 3-D points specified in xq, yq, and zq.

example

EHintrp = interpolateHarmonicField(harmonicresults,querypoints) returns the interpolated electric or magnetic field values at the points specified in querypoints.

example

Examples

collapse all

Open Live Script

Solve a simple scattering problem and interpolate the x-component of the resulting electric field. A scattering problem computes the waves reflected by a square object illuminated by incident waves.

Specify the wave number k=ω/α as 4π.

k = 4*pi;

Represent the square surface with a diamond-shaped hole. Define a diamond in a square, place them in one matrix, and create a set formula that subtracts the diamond from the square.

square = [3; 4; -5; -5; 5; 5; -5; 5; 5; -5];
diamond = [2; 4; 2.1; 2.4; 2.7; 2.4; 1.5; 1.8; 1.5; 1.2];
gd = [square,diamond];
ns = char('square','diamond')';
sf = 'square - diamond';

Create the geometry.

g = decsg(gd,sf,ns);

Plot the geometry with the edge labels.

figure; 
pdegplot(g,EdgeLabels="on"); 
xlim([-6,6])
ylim([-6,6])

Figure contains an axes object. The axes object contains 9 objects of type line, text.

Create an femodel object for harmonic electromagnetic analysis with the electric field type. Include the geometry into the model.

model = femodel(AnalysisType="electricHarmonic", ...
                Geometry=g);

Specify the vacuum permittivity and permeability values as 1.

model.VacuumPermittivity = 1;
model.VacuumPermeability = 1;

Specify the relative permittivity, relative permeability, and conductivity of the material.

model.MaterialProperties = ...
    materialProperties(RelativePermittivity=1, ...
                       RelativePermeability=1, ...
                       ElectricalConductivity=0);

Apply the absorbing boundary condition on the edges of the square. Specify the thickness and attenuation rate for the absorbing region by using the Thickness, Exponent, and Scaling arguments.

ffbc = farFieldBC(Thickness=2,Exponent=4,Scaling=1);
model.EdgeBC(1:4) = edgeBC(FarField=ffbc);

Apply the boundary condition on the edges of the diamond.

innerBCFunc = @(location,~) [-exp(-1i*k*location.x); ...
                            zeros(1,length(location.x))];
model.EdgeBC(5:8) = edgeBC(ElectricField=innerBCFunc);

Generate a mesh.

model = generateMesh(model,Hmax=0.1);

Solve the harmonic analysis model for the frequency k = 4π.

R = solve(model,k);

Plot the real part of the x-component of the resulting electric field.

u = R.ElectricField;

figure
pdeplot(R.Mesh,XYData=real(u.Ex));
colormap(jet)

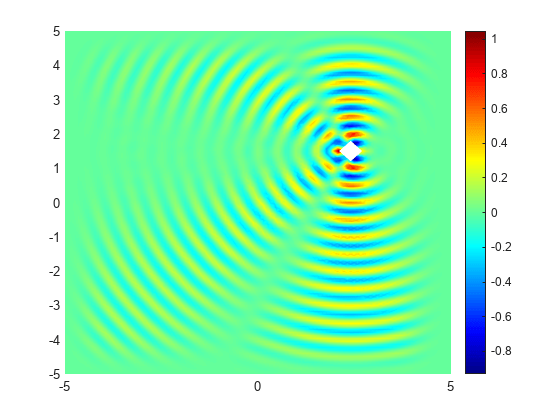
Figure contains an axes object. The axes object contains an object of type patch.

Interpolate the resulting electric field to a grid covering the portion of the geometry, for x and y from -1 to 4.

v = linspace(-1,4,101);
[X,Y] = meshgrid(v);
Eintrp = interpolateHarmonicField(R,X,Y);

Reshape Eintrp.Ex and plot the x-component of the resulting electric field.

EintrpX = reshape(Eintrp.ElectricField.Ex,size(X));

figure
surf(X,Y,real(EintrpX),LineStyle="none");
view(0,90)
colormap(jet)

Figure contains an axes object. The axes object contains an object of type surface.

Open Live Script

Interpolate the x-component of the magnetic field in a harmonic analysis of a 3-D model.

Create an femodel object for harmonic electromagnetic analysis with the magnetic field type. Include the geometry representing a plate with a hole into the model.

model = femodel(AnalysisType="magneticHarmonic", ...
                Geometry="PlateHoleSolid.stl");

Plot the geometry.

pdegplot(model,FaceLabels="on",FaceAlpha=0.3)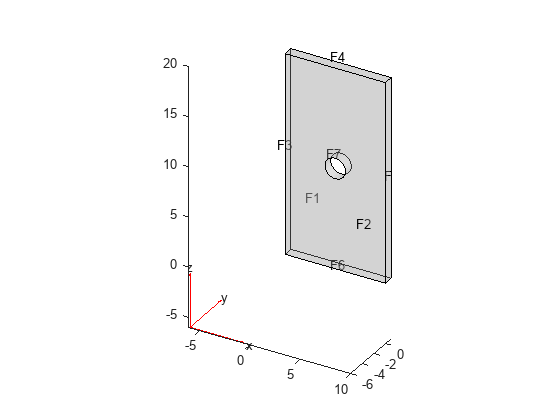

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Specify the vacuum permittivity and permeability values in the SI system of units.

model.VacuumPermittivity = 8.8541878128E-12;
model.VacuumPermeability = 1.2566370614E-6;

Specify the relative permittivity, relative permeability, and conductivity of the material.

model.MaterialProperties = ...
    materialProperties(RelativePermittivity=1, ...
                       RelativePermeability=6, ...
                       ElectricalConductivity=60);

Specify the current density for the entire geometry. For harmonic analysis with the magnetic field type, the toolbox uses the curl of the specified current density.

model.CellLoad = cellLoad(CurrentDensity=[1;1;1]);

Apply the absorbing boundary condition with a thickness of 0.1 on the side faces.

ffbc = farFieldBC(Thickness=0.1);
model.FaceBC(3:6) = faceBC(FarField=ffbc);

Specify the magnetic field on the face bordering the round hole in the center of the geometry.

model.FaceBC(7) = faceBC(MagneticField=[1000;0;0]);

Generate a mesh.

model = generateMesh(model);

Solve the model for a frequency of 50.

result = solve(model,50);

Plot the real part of the x-component of the resulting magnetic field.

u = result.MagneticField;
figure
pdeplot3D(result.Mesh,ColorMapData=real(u.Hx));
colormap jet
title("Real Part of x-Component of Magnetic Field")

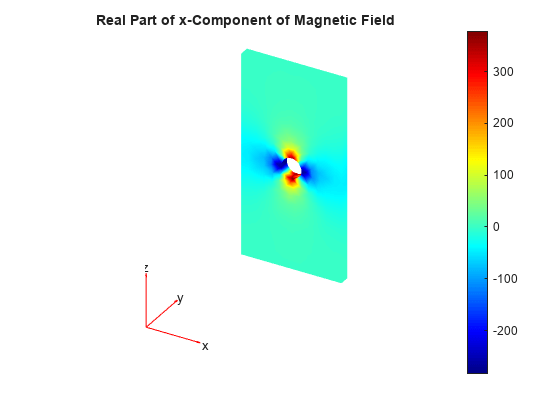
Figure contains an axes object. The hidden axes object with title Real Part of x-Component of Magnetic Field contains 5 objects of type patch, quiver, text.

Interpolate the resulting magnetic field to a grid covering the central portion of the geometry, for x, y, and z.

x = linspace(3,7,51);
y = linspace(0,1,51);
z = linspace(8,12,51);
[X,Y,Z] = meshgrid(x,y,z);

Hintrp = interpolateHarmonicField(result,X,Y,Z)
Hintrp = struct with fields:
    MagneticField: [1x1 FEStruct]

Reshape Hintrp.Hx and plot the x-component of the resulting magnetic field as a slice plot for y = 0.

HintrpX = reshape(Hintrp.MagneticField.Hx,size(X));

figure
slice(X,Y,Z,real(HintrpX),[],0,[],"cubic")
axis equal
colorbar
colormap(jet)

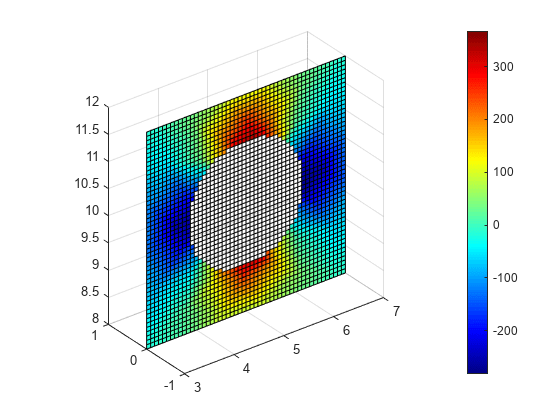
Figure contains an axes object. The axes object contains an object of type surface.

Alternatively, you can specify the grid by using a matrix of query points.

querypoints = [X(:),Y(:),Z(:)]';
Hintrp = interpolateHarmonicField(result,querypoints)
Hintrp = struct with fields:
    MagneticField: [1x1 FEStruct]

Input Arguments

collapse all

Solution of a harmonic electromagnetic problem, specified as a HarmonicResults object. Create harmonicresults using the solve function.

x-coordinate query points, specified as a real array. interpolateHarmonicField evaluates the electric or magnetic field at the 2-D coordinate points [xq(i) yq(i)] or at the 3-D coordinate points [xq(i) yq(i) zq(i)] for every index i.Therefore, xq, yq, and (if present) zq must have the same number of entries.

interpolateHarmonicField converts the query points to column vectors xq(:), yq(:), and (if present) zq(:). It returns electric or magnetic field values as a column vector of the same size. To ensure that the dimensions of the returned solution are consistent with the dimensions of the original query points, use reshape. For example, use EHintrpX = reshape(EHintrp.Ex,size(xq)).

Example: xq = [0.5 0.5 0.75 0.75]

Data Types: double

y-coordinate query points, specified as a real array. interpolateHarmonicField evaluates the electric or magnetic field at the 2-D coordinate points [xq(i) yq(i)] or at the 3-D coordinate points [xq(i) yq(i) zq(i)] for every index i. Therefore, xq, yq, and (if present) zq must have the same number of entries.

interpolateHarmonicField converts the query points to column vectors xq(:), yq(:), and (if present) zq(:). It returns electric or magnetic field values as a column vector of the same size. To ensure that the dimensions of the returned solution are consistent with the dimensions of the original query points, use reshape. For example, use EHintrpY = reshape(EHintrp.Ey,size(yq)).

Example: yq = [1 2 0 0.5]

Data Types: double

z-coordinate query points, specified as a real array. interpolateHarmonicField evaluates the electric or magnetic field at the 3-D coordinate points [xq(i) yq(i) zq(i)] for every index i. Therefore, xq, yq, and zq must have the same number of entries.

interpolateHarmonicField converts the query points to column vectors xq(:), yq(:), and zq(:). It returns electric or magnetic field values as a column vector of the same size. To ensure that the dimensions of the returned solution are consistent with the dimensions of the original query points, use reshape. For example, use EHintrpZ = reshape(EHintrp.Ez,size(zq)).

Example: zq = [1 1 0 1.5]

Data Types: double

Query points, specified as a real matrix with either two rows for a 2-D geometry or three rows for a 3-D geometry. interpolateHarmonicField evaluates the electric or magnetic field at the coordinate points querypoints(:,i) for every index i, so each column of querypoints contains exactly one 2-D or 3-D query point.

Example: For a 2-D geometry, querypoints = [0.5 0.5 0.75 0.75; 1 2 0 0.5]

Data Types: double

Output Arguments

collapse all

Electric or magnetic field at query points, returned as an FEStruct object with the properties representing the spatial components of the electric or magnetic field at the query points. For query points that are outside the geometry, EHintrp.Ex(i), EHintrp.Ey(i), EHintrp.Ez(i), EHintrp.Hx(i), EHintrp.Hy(i), and EHintrp.Hz(i) are NaN. Properties of an FEStruct object are read-only.

Version History

Introduced in R2022a

See Also

Objects

Functions