specifyCoefficients

Specify coefficients in PDE model

Syntax

specifyCoefficients(model,m=m,d=d,c=c,a=a,f=f)

specifyCoefficients(model,m=m,d=d,c=c,a=a,f=f,RegionType=RegionID)

CA = specifyCoefficients(___)

Description

specifyCoefficients(model,m=m,d=d,c=c,a=a,f=f) defines the PDE coefficients and includes them in model. You must specify coefficients: m, d, c, a, and f. This syntax applies coefficients to the entire geometry.

Note

Include a geometry in model before using specifyCoefficients.

example

specifyCoefficients(model,m=m,d=d,c=c,a=a,f=f,RegionType=RegionID) assigns coefficients for a specified geometry region.

example

CA = specifyCoefficients(___) returns a handle to the coefficient assignment object in model.

example

Examples

collapse all

Specify Poisson's Equation

Open Live Script

Specify the coefficients for Poisson's equation $- \nabla \cdot \nabla u = 1$ .

solvepde addresses equations of the form

$m \frac{\partial^{2} u}{\partial t^{2}} + d \frac{\partial u}{\partial t} - \nabla \cdot (c \nabla u) + a u = f$ .

Therefore, the coefficients for Poisson's equation are $m = 0$ , $d = 0$ , $c = 1$ , $a = 0$ , $f = 1$ . Include these coefficients in a PDE model of the L-shaped membrane.

model = createpde();
geometryFromEdges(model,@lshapeg);
specifyCoefficients(model,"m",0,...
                          "d",0,...
                          "c",1,...
                          "a",0,...
                          "f",1);

Specify zero Dirichlet boundary conditions, mesh the model, and solve the PDE.

applyBoundaryCondition(model,"dirichlet", ...
                             "Edge",1:model.Geometry.NumEdges, ...
                             "u",0);
generateMesh(model,"Hmax",0.25);
results = solvepde(model);

View the solution.

pdeplot(model,"XYData",results.NodalSolution)

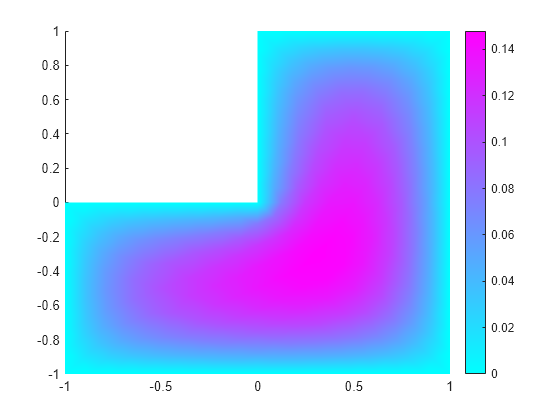
Figure contains an axes object. The axes object contains an object of type patch.

Coefficient Handle for Nonconstant Coefficients

Open Live Script

Specify coefficients for Poisson's equation in 3-D with a nonconstant source term, and obtain the coefficient object.

The equation coefficients are $m = 0$ , $d = 0$ , $c = 1$ , $a = 0$ . For the nonconstant source term, take $f = y^{2} \tanh (z) / 1000$ .

f = @(location,state)location.y.^2.*tanh(location.z)/1000;

Set the coefficients in a 3-D rectangular block geometry.

model = createpde();
importGeometry(model,"Block.stl");
CA = specifyCoefficients(model,"m",0,...
                               "d",0,...
                               "c",1,...
                               "a",0,...
                               "f",f)

CA = 
  CoefficientAssignment with properties:

    RegionType: 'cell'
      RegionID: 1
             m: 0
             d: 0
             c: 1
             a: 0
             f: @(location,state)location.y.^2.*tanh(location.z)/1000

Set zero Dirichlet conditions on face 1, mesh the geometry, and solve the PDE.

applyBoundaryCondition(model,"dirichlet","Face",1,"u",0);
generateMesh(model);
results = solvepde(model);

View the solution on the surface.

pdeplot3D(model,"ColorMapData",results.NodalSolution)

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

Specify Coefficients Depending on Subdomain

Open Live Script

Create a scalar PDE model with the L-shaped membrane as the geometry. Plot the geometry and subdomain labels.

model = createpde();
geometryFromEdges(model,@lshapeg);
pdegplot(model,"FaceLabels","on")
axis equal
ylim([-1.1,1.1])

Figure contains an axes object. The axes object contains 4 objects of type line, text.

Set the c coefficient to 1 in all domains, but the f coefficient to 1 in subdomain 1, 5 in subdomain 2, and -8 in subdomain 3. Set all other coefficients to 0.

specifyCoefficients(model,"m",0,"d",0,"c",1,"a",0,"f",1,"Face",1);
specifyCoefficients(model,"m",0,"d",0,"c",1,"a",0,"f",5,"Face",2);
specifyCoefficients(model,"m",0,"d",0,"c",1,"a",0,"f",-8,"Face",3);

Set zero Dirichlet boundary conditions to all edges. Create a mesh, solve the PDE, and plot the result.

applyBoundaryCondition(model,"dirichlet", ...
                             "Edge",1:model.Geometry.NumEdges, ...
                             "u",0);
generateMesh(model,"Hmax",0.25);
results = solvepde(model);
pdeplot(model,"XYData",results.NodalSolution)

Figure contains an axes object. The axes object contains an object of type patch.

Damped Cantilever Beam

Open Live Script

Perform transient analysis of a simple cantilever beam with and without damping. To include damping in the analysis, specify nonzero m and d coefficients.

Create a geometry representing a cantilever beam. The beam is 5 inches long and 0.1 inch thick.

height = 0.1;
width = 5;
gm = [3;4;0;width;width;0;0;0;height;height];
g = decsg(gm,'S1',('S1')');

Create a PDEModel object with two independent variables, and include a geometry in the model.

model = createpde(2);
geometryFromEdges(model,g);

Plot the geometry with edge labels.

pdegplot(model,EdgeLabels="on")

Figure contains an axes object. The axes object contains 5 objects of type line, text.

Specify that the left edge of the beam is a fixed boundary.

applyBoundaryCondition(model,"dirichlet",Edge=4,u=[0,0]);

Specify Young's modulus, Poisson's ratio, and the mass density of the beam assuming that it is made of steel.

E = 3.0e7;
nu = 0.3;
rho = 0.3/386;

Specify the PDE coefficients for the undamped model by setting the d coefficient to 0.

G = E/(2.*(1+nu));
mu = 2.0*G*nu/(1-nu);
specifyCoefficients(model, ...
                    m=rho, ...
                    d=0, ...
                    c=[2*G+mu;0;G;0;G;mu;0;G;0;2*G+mu], ...
                    a=0, ...
                    f=[0;0]);

Set the initial displacement to $(0; 10^{- 4} x^{2})$ and the initial velocity to (0; 0).

setInitialConditions(model,@(location) location.x.^2.*[0;0.0001],[0;0]);

Generate a mesh and solve the problem.

generateMesh(model);
tlist = 0:0.25/1000:0.25;
tres = solvepde(model,tlist);

Plot the undamped solution.

uu = tres.NodalSolution;
utip = uu(2,2,:);
plot(tlist,utip(:))

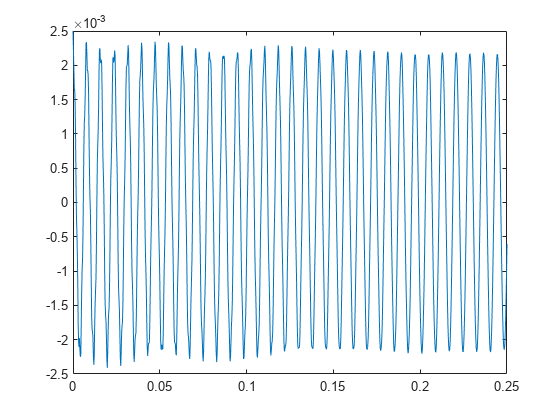
Figure contains an axes object. The axes object contains an object of type line.

Obtain assembled mass and stiffness matrices by calling assembleFEMatrices.

fem = assembleFEMatrices(model);

Now specify the coefficients for the beam model with Rayleigh damping. The d coefficient represents the damping matrix. The d coefficient is a linear combination of the mass matrix fem.M and the stiffness matrix fem.K.

alpha = 10;
beta = 0;
dampmat = alpha*fem.M + beta*fem.K;
specifyCoefficients(model, ...
                    m=rho, ...
                    d=dampmat, ...
                    c=[2*G+mu;0;G;0;G;mu;0;G;0;2*G+mu], ...
                    a=0, ...
                    f=[0;0]);

Solve the problem and plot the damped solution.

tres = solvepde(model,tlist);
uu = tres.NodalSolution;
utip = uu(2,2,:);
plot(tlist,utip(:))

Figure contains an axes object. The axes object contains an object of type line.

Input Arguments

collapse all

`model` — PDE model
`PDEModel` object

PDE model, specified as a PDEModel object.

Example: model = createpde

`m` — Second-order time derivative coefficient
scalar | column vector | function handle

Second-order time derivative coefficient, specified as a scalar, column vector, or function handle. For details on the sizes, and for details of the function handle form of the coefficient, see m, d, or a Coefficient for specifyCoefficients.

Specify 0 on the entire geometry if the term is not part of your problem. If this coefficient is zero in one subdomain of the geometry, it must be zero on the entire geometry.

Example: specifyCoefficients("m",@mcoef,"d",0,"c",1,"a",0,"f",1,"Face",1:4)

Data Types: double | function_handle
Complex Number Support: Yes

`d` — First-order time derivative coefficient
scalar | column vector | function handle

First-order time derivative coefficient, specified as a scalar, column vector, or function handle. For details on the sizes, and for details of the function handle form of the coefficient, see m, d, or a Coefficient for specifyCoefficients.

Note

If the m coefficient is nonzero, d must be 0 or a matrix, and not a function handle. See d Coefficient When m Is Nonzero.

Specify 0 on the entire geometry if the term is not part of your problem. If this coefficient is zero in one subdomain of the geometry, it must be zero on the entire geometry.

Example: specifyCoefficients("m",0,"d",@dcoef,"c",1,"a",0,"f",1,"Face",1:4)

Data Types: double | function_handle
Complex Number Support: Yes

`c` — Second-order space derivative coefficient
scalar | column vector | function handle

Second-order space derivative coefficient, specified as a scalar, column vector, or function handle. For details on the sizes, and for details of the function handle form of the coefficient, see c Coefficient for specifyCoefficients.

This coefficient must not be zero in one subdomain of the geometry while nonzero in another subdomain.

Example: specifyCoefficients("m",0,"d",0,"c",@ccoef,"a",0,"f",1,"Face",1:4)

Data Types: double | function_handle
Complex Number Support: Yes

`a` — Solution multiplier coefficient
scalar | column vector | function handle

Solution multiplier coefficient, specified as a scalar, column vector, or function handle. For details on the sizes, and for details of the function handle form of the coefficient, see m, d, or a Coefficient for specifyCoefficients.

Specify 0 if the term is not part of your problem. This coefficient can be zero in one subdomain and nonzero in another.

Example: specifyCoefficients("m",0,"d",0,"c",1,"a",@acoef,"f",1,"Face",1:4)

Data Types: double | function_handle
Complex Number Support: Yes

`f` — Source coefficient
scalar | column vector | function handle

Source coefficient, specified as a scalar, column vector, or function handle. For details on the sizes, and for details of the function handle form of the coefficient, see f Coefficient for specifyCoefficients.

Specify 0 if the term is not part of your problem. This coefficient can be zero in one subdomain and nonzero in another.

Example: specifyCoefficients("m",0,"d",0,"c",1,"a",0,"f",@fcoeff,"Face",1:4)

Data Types: double | function_handle
Complex Number Support: Yes

`RegionType` — Geometric region type
`Face` for a 2-D model | `Cell` for a 3-D model

Geometric region type, specified as Face or Cell.

Example: specifyCoefficients(m=0,d=0,c=1,a=0,f=10,Cell=2)

Data Types: char | string

`RegionID` — Geometric region ID
positive integer | vector of positive integers

Geometric region ID, specified as a positive integer or vector of positive integers. Find the region IDs by using pdegplot.

Example: specifyCoefficients(m=0,d=0,c=1,a=0,f=10,Cell=1:3)

Data Types: double

Output Arguments

collapse all

`CA` — Coefficient assignment
`CoefficientAssignment` object

Coefficient assignment, returned as a CoefficientAssignment object. See CoefficientAssignment Properties.

More About

collapse all

PDE Coefficients

solvepde solves PDEs of the form

$m \frac{\partial^{2} u}{\partial t^{2}} + d \frac{\partial u}{\partial t} - \nabla \cdot (c \nabla u) + a u = f$

solvepdeeig solves PDE eigenvalue problems of the form

$\begin{array}{l} - \nabla \cdot (c \nabla u) + a u = λ d u \\ or \\ - \nabla \cdot (c \nabla u) + a u = λ^{2} m u \end{array}$

specifyCoefficients defines the coefficients m, d, c, a, and f in the PDE model.

`d` Coefficient When `m` Is Nonzero

The d coefficient takes a special matrix form when m is nonzero. You must specify d as a matrix of a particular size, not as a function handle.

In the case of nonzero m, the d coefficient represents a damping matrix. To specify d, perform these two steps:

Assemble finite element matrices for the PDE problem with your original coefficients and d = 0 by calling assembleFEMatrices. Use the default "none" method for assembleFEMatrices.

model = createpde();
geometryFromEdges(model,@lshapeg);
generateMesh(model,Hmax=0.25);

specifyCoefficients(model,m=1,d=0,c=1,a=0,f=0,Face=1);
specifyCoefficients(model,m=1,d=0,c=1,a=0,f=2,Face=2);
specifyCoefficients(model,m=1,d=0,c=1,a=0,f=-8,Face=3);
results = assembleFEMatrices(model);

Define the d coefficient as a matrix of size results.M. Generally, d is either proportional to results.M or is a linear combination of results.M and results.K.

specifyCoefficients(model,m=1,d=0*results.M,c=1,a=0,f=0,Face=1);
specifyCoefficients(model,m=1,d=1*results.M, ... % nonzero d
                          c=1,a=0,f=2,Face=2);
specifyCoefficients(model,m=1,d=0*results.M,c=1,a=0,f=-8,Face=3);

For an example with nonzero m and d coefficients, see Damped Cantilever Beam.

Tips

For eigenvalue equations, the coefficients cannot depend on the solution u or its gradient.
You can transform a partial differential equation into the required form by using Symbolic Math Toolbox™. The pdeCoefficients (Symbolic Math Toolbox) function converts a PDE into the required form and extracts the coefficients into a structure that can be used by specifyCoefficients.
The pdeCoefficients function also can return a structure of symbolic expressions, in which case you need to use pdeCoefficientsToDouble (Symbolic Math Toolbox) to convert these expressions to double format before passing them to specifyCoefficients.

Version History

Introduced in R2016a

specifyCoefficients

Syntax

Description

Examples

Specify Poisson's Equation

Coefficient Handle for Nonconstant Coefficients

Specify Coefficients Depending on Subdomain

Damped Cantilever Beam

Input Arguments

`model` — PDE model
`PDEModel` object

`m` — Second-order time derivative coefficient
scalar | column vector | function handle

`d` — First-order time derivative coefficient
scalar | column vector | function handle

`c` — Second-order space derivative coefficient
scalar | column vector | function handle

`a` — Solution multiplier coefficient
scalar | column vector | function handle

`f` — Source coefficient
scalar | column vector | function handle

`RegionType` — Geometric region type
`Face` for a 2-D model | `Cell` for a 3-D model

`RegionID` — Geometric region ID
positive integer | vector of positive integers

Output Arguments

`CA` — Coefficient assignment
`CoefficientAssignment` object

More About

PDE Coefficients

`d` Coefficient When `m` Is Nonzero

Tips

Version History

See Also

Topics

specifyCoefficients

Syntax

Description

Examples

Specify Poisson's Equation

Coefficient Handle for Nonconstant Coefficients

Specify Coefficients Depending on Subdomain

Damped Cantilever Beam

Input Arguments

model — PDE model PDEModel object

m — Second-order time derivative coefficient scalar | column vector | function handle

d — First-order time derivative coefficient scalar | column vector | function handle

c — Second-order space derivative coefficient scalar | column vector | function handle

a — Solution multiplier coefficient scalar | column vector | function handle

f — Source coefficient scalar | column vector | function handle

RegionType — Geometric region type Face for a 2-D model | Cell for a 3-D model

RegionID — Geometric region ID positive integer | vector of positive integers

Output Arguments

CA — Coefficient assignment CoefficientAssignment object

More About

PDE Coefficients

d Coefficient When m Is Nonzero

Tips

Version History

See Also

Topics

`model` — PDE model
`PDEModel` object

`m` — Second-order time derivative coefficient
scalar | column vector | function handle

`d` — First-order time derivative coefficient
scalar | column vector | function handle

`c` — Second-order space derivative coefficient
scalar | column vector | function handle

`a` — Solution multiplier coefficient
scalar | column vector | function handle

`f` — Source coefficient
scalar | column vector | function handle

`RegionType` — Geometric region type
`Face` for a 2-D model | `Cell` for a 3-D model

`RegionID` — Geometric region ID
positive integer | vector of positive integers

`CA` — Coefficient assignment
`CoefficientAssignment` object

`d` Coefficient When `m` Is Nonzero