pdeCoefficientsToDouble

Create a symbolic PDE that represents the Laplacian of the variable u(x,y).

syms u(x,y) f
pdeeq = laplacian(u,[x y]) == f

pdeeq(x, y) = 
$$\frac{{\partial }^2}{\partial x^2}\mathrm{ }u\left(x,y\right)+\frac{{\partial }^2}{\partial y^2}\mathrm{ }u\left(x,y\right)=f$$

Extract the coefficients of the PDE as symbolic expressions and display their values.

symCoeffs = pdeCoefficients(pdeeq,u,'Symbolic',true);
structfun(@disp,symCoeffs)

$$0$$

$$0$$

$$\left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)$$

$$f$$

$$0$$

pdeCoefficients converts the symbolic PDE into a scalar PDE equation of the form

$$m\frac{{\partial }^{2}u}{\partial t^2}+d\frac{\partial u}{\partial t}-\nabla \cdot (c\nabla u)+au=f$$,

and extract the coefficients a, c, m, d, and f into the structure symCoeffs.

Choose a value for f. Since symCoeffs are symbolic objects, use pdeCoefficientsToDouble to convert the coefficients to double data type. The coefficients with double data type are valid inputs for the specifyCoefficients function in the PDE Toolbox.

symCoeffs = subs(symCoeffs,f,-3);
coeffs = pdeCoefficientsToDouble(symCoeffs)

coeffs = struct with fields:
    a: 0
    c: [4x1 double]
    m: 0
    d: 0
    f: -3

Solve a system of two second-order PDEs. You can solve the PDE system by extracting the PDE coefficients symbolically using pdeCoefficients, converting the coefficients to double-precision numbers using pdeCoefficientsToDouble, and specifying the coefficients in the PDE model using specifyCoefficients.

The system of PDEs represents the deflection of a clamped structural plate under a uniform pressure load. The system of PDEs with the dependent variables $$u_1$$ and $$u_2$$ is given by

$$-{\nabla }^2{u}_1+u_2=0$$,

$$-D{\nabla }^2{u}_2=p$$,

where $$D$$ is the bending stiffness of the plate given by

$$D=\frac{E{h}^3}{12(1-{\nu }^2)}$$,

and $$E$$ is the modulus of elasticity, $$\nu$$ is Poisson's ratio, $$h$$ is the plate thickness, $$u_1$$ is the transverse deflection of the plate, and $$p$$ is the pressure load.

Create a PDE model for the system of two equations.

model = createpde(2);

Create a square geometry. Specify the side length of the square. Then include the geometry in the PDE model.

len = 10.0;
gdm = [3 4 0 len len 0 0 0 len len]';
g = decsg(gdm,'S1',('S1')');
geometryFromEdges(model,g);

Specify the values of the physical parameters of the system. Let the external pressure $$p$$ be a symbolic variable pres that can take any value.

E = 1.0e6;
h_thick = 0.1;
nu = 0.3;
D = E*h_thick^3/(12*(1 - nu^2));
syms pres

Declare the PDE system as a system symbolic equations. Extract the coefficients of the PDE and return them in symbolic form.

syms u1(x,y) u2(x,y)
pdeeq = [-laplacian(u1) + u2; -D*laplacian(u2) - pres];
symCoeffs = pdeCoefficients(pdeeq,[u1 u2],'Symbolic',true)

symCoeffs = struct with fields:
    m: 0
    a: [2x2 sym]
    c: [4x4 sym]
    f: [2x1 sym]
    d: 0

Display the coefficients m, a, c, f, and d.

structfun(@disp,symCoeffs)

$$0$$

$$\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)$$

$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& \frac{25000}{273}& 0\\ 0& 0& 0& \frac{25000}{273}\end{array}\right)$$

$$\left(\begin{array}{c}0\\ \mathrm{pres}\end{array}\right)$$

$$0$$

Substitute a value for pres using the subs function. Since the outputs of subs are symbolic objects, use the pdeCoefficientsToDouble function to convert the coefficients to the double data type, which makes them valid inputs for the PDE Toolbox.

symCoeffs = subs(symCoeffs,pres,2);
coeffs = pdeCoefficientsToDouble(symCoeffs)

coeffs = struct with fields:
    a: [4x1 double]
    c: [16x1 double]
    m: 0
    d: 0
    f: [2x1 double]

Specify the PDE coefficients for the PDE model.

specifyCoefficients(model,'m',coeffs.m,'d',coeffs.d, ...
    'c',coeffs.c,'a',coeffs.a,'f',coeffs.f);

Specify spring stiffness. Specify boundary conditions by defining distributed springs on all four edges.

k = 1e7;
bOuter = applyBoundaryCondition(model,'neumann','Edge',(1:4), ...
    'g',[0 0],'q',[0 0; k 0]);

Specify the mesh size of the geometry and generate a mesh for the PDE model.

hmax = len/20;
generateMesh(model,'Hmax',hmax);

Solve the model.

res = solvepde(model);

Access the solution at the nodal locations.

u = res.NodalSolution;

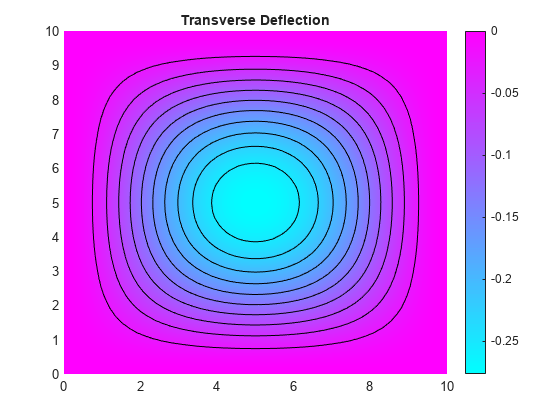
Plot the transverse deflection of the plate.

numNodes = size(model.Mesh.Nodes,2);
figure;
pdeplot(model,'XYData',u(1:numNodes),'contour','on')
title 'Transverse Deflection'

Find the transverse deflection at the plate center.

wMax = min(u(1:numNodes,1))

wMax = 
-0.2763

Compare the result with the deflection at the plate center computed analytically.

pres = 2;
wMax = -.0138*pres*len^4/(E*h_thick^3)

wMax = 
-0.2760

Since R2023a

Create a PDE system of four equations with four dependent variables, $\mathit{A}$, $\mathit{E}$, $\mathit{P}$, and $\mathit{T}$.

syms A(x,y,z,t) E(x,y,z,t) P(x,y,z,t) T(x,y,z,t)
eqn1 = diff(A,t) == -A*E*(-exp(T));
eqn2 = diff(P,t) == -P*E*(-exp(T));
eqn3 = diff(E,t) == -A*E*(-exp(T)) - P*E*(-exp(T));
eqn4 = diff(T,t) == laplacian(T,[x y z]) + A*E*(-exp(T)) + P*E*(-exp(T));
pdeeq = [eqn1; eqn2; eqn3; eqn4]

pdeeq(x, y, z, t) = 
$$\begin{array}{l}\left(\begin{array}{c}\frac{\partial }{\partial t}\mathrm{ }A\left(x,y,z,t\right)={\sigma }_2\\ \frac{\partial }{\partial t}\mathrm{ }P\left(x,y,z,t\right)={\sigma }_1\\ \frac{\partial }{\partial t}\mathrm{ }\text{E}\left(x,y,z,t\right)={\sigma }_2+{\sigma }_1\\ \frac{\partial }{\partial t}\mathrm{ }T\left(x,y,z,t\right)=\frac{{\partial }^2}{\partial x^2}\mathrm{ }T\left(x,y,z,t\right)+\frac{{\partial }^2}{\partial y^2}\mathrm{ }T\left(x,y,z,t\right)+\frac{{\partial }^2}{\partial z^2}\mathrm{ }T\left(x,y,z,t\right)-{\sigma }_2-{\sigma }_1\end{array}\right)\\ \\ \mathrm{where}\\ \\ \mathrm{ }{\sigma }_1={\mathrm{e}}^{T\left(x,y,z,t\right)}\hspace{0.17em}\text{E}\left(x,y,z,t\right)\hspace{0.17em}P\left(x,y,z,t\right)\\ \\ \mathrm{ }{\sigma }_2={\mathrm{e}}^{T\left(x,y,z,t\right)}\hspace{0.17em}A\left(x,y,z,t\right)\hspace{0.17em}\text{E}\left(x,y,z,t\right)\end{array}$$

Extract the coefficients of the PDE system as symbolic expressions. Specify the variable u to represent the dependent variables.

u = [A E P T];
symCoeffs = pdeCoefficients(pdeeq,u,'Symbolic',true)

symCoeffs = struct with fields:
    m: [4x4 sym]
    a: [4x4 sym]
    c: [12x12 sym]
    f: [4x1 sym]
    d: [4x4 sym]

Display the coefficients m, a, c, f, and d.

structfun(@disp,symCoeffs)

$$\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

$$\begin{array}{l}\left(\begin{array}{cccc}-{\sigma }_2& 0& 0& 0\\ 0& {\sigma }_1& 0& 0\\ -{\sigma }_2& {\sigma }_1& 0& 0\\ {\sigma }_2& {\mathrm{e}}^{T\left(x,y,z,t\right)}\hspace{0.17em}P\left(x,y,z,t\right)& 0& 0\end{array}\right)\\ \\ \mathrm{where}\\ \\ \mathrm{ }{\sigma }_1=-{\mathrm{e}}^{T\left(x,y,z,t\right)}\hspace{0.17em}P\left(x,y,z,t\right)\\ \\ \mathrm{ }{\sigma }_2={\mathrm{e}}^{T\left(x,y,z,t\right)}\hspace{0.17em}\text{E}\left(x,y,z,t\right)\end{array}$$

$$\left(\begin{array}{cccccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right)$$

$$\left(\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right)$$

$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right)$$

Convert the coefficients to the double data type so that they are valid inputs for the specifyCoefficients function in Partial Differential Equation Toolbox. Because the a coefficient in symCoeffs contains the dependent variables and is not constant, calling pdeCoefficientsToDouble(symCoeffs) without the second input argument can return an error. Instead, specify the second argument as the dependent variables u when using pdeCoefficientsToDouble.

coeffs = pdeCoefficientsToDouble(symCoeffs,u)

coeffs = struct with fields:
    a: @makeCoefficient/coefficientFunction
    c: [144x1 double]
    m: 0
    d: [16x1 double]
    f: 0