Neural Network for Beam Selection

This example uses:

This example shows how to use a neural network to reduce the overhead in the beam selection task. In the example, you use only the location of the receiver rather than knowledge of the communication channels. Instead of an exhaustive beam search over all the beam pairs, you can reduce beam sweeping overhead by searching among the selected $K$ beam pairs. Considering a system with a total of 70 beam pairs, simulation results show that the designed machine learning algorithm can achieve an accuracy of 90% by performing an exhaustive search over less than half of the beam pairs. For the simulation, the example considers an urban macrocell (UMa) scenario, as defined in TR 38.901 and TR 38.843.

Introduction

To enable millimeter wave (mmWave) communications, beam management techniques must be used due to the high pathloss and blockage experienced at high frequencies. Beam management is a set of Layer 1 (physical layer) and Layer 2 (medium access control) procedures to establish and retain an optimal beam pair (transmit beam and a corresponding receive beam) for good connectivity. For simulations of 5G New Radio (NR) beam management procedures, see the NR SSB Beam Sweeping (5G Toolbox) and NR Downlink Transmit-End Beam Refinement Using CSI-RS (5G Toolbox) examples.

This example considers beam selection procedures when a connection is established between the user equipment (UE) and access network node (gNB). In 5G NR, the beam selection procedure for initial access consists of beam sweeping, which requires exhaustive searches over all the beams on the transmitter and the receiver sides, and then selection of the beam pair offering the strongest reference signal received power (RSRP). Since mmWave communications require many antenna elements, implying many beams, an exhaustive search over all beams becomes computationally expensive and increases the initial access time.

To avoid repeatedly performing an exhaustive search and to reduce the communication overhead, machine learning has been applied to the beam selection problem. Typically, the beam selection problem is posed as a classification task, where the target output is the best beam pair index. The extrinsic information, including lidar, GPS signals, and roadside camera images, is used as input to the machine learning algorithms. Specifically, given this out-of-band information, a trained machine learning model recommends a set of $K$ good beam pairs. Instead of an exhaustive search over all the beam pairs, the simulation reduces beam sweeping overhead by searching only among the selected $K$ beam pairs.

This example uses a neural network to perform beam selection using only the 3D coordinates of the UE and a channel model compliant with the definition in TR 38.901. The example consists of these steps:

Generate a set of training samples, where each sample consists of a UE location and the true optimal beam pair index (found by performing exhaustive search over all the beam pairs at transmit and receive ends).
Design and train a neural network that uses the UE location as the input and the true optimal beam pair index as the correct label.
Run the neural network with a set of testing samples. During this phase, the neural network outputs $K$ good beam pairs.
Perform an exhaustive search over the $K$ good beam pairs from the above step. Select the beam pair with the highest average RSRP as the final predicted beam pair by the neural network.

The example measures the effectiveness of the proposed method using two metrics: average RSRP and top-K accuracy. This figure shows the main processing steps.

Generate Training and Test Data

In the prerecorded data, a channel is simulated where UEs are randomly distributed inside the first sector of a three-sector cell, as discussed in TR 38.901. The example uses the baseline system-level simulation assumptions for AI/ML from TR 38.843 Table 6.3.1-1. The number of transmit and receive beams depends on the half-power beamwidth. While minimizing the number of beams, the example selects enough beams to cover the full area. By default, the example considers ten transmit beams and seven receive beams, according to the antenna specifications defined in TR 38.843 Table 6.3.1-1. After the TR 38.901 channel is set up, the example considers 15,000 different UE locations in the training set and 500 different UE locations in the test set. For each location, the example performs SSB-based beam sweeping for an exhaustive search over all 70 beam pairs and determines the true optimal beam pair by picking the beam pair with the highest average RSRP.

To generate new training and test sets, you can adjust the useSavedData and SaveData checkboxes.

useSavedData = true;
saveData     = false;
if useSavedData
    load nnBS_prm.mat;              % Load beam selection system parameters
    load nnBS_TrainingData.mat;     % Load prerecorded training samples
    %   (input: receiver's location; output: optimal beam pair indices)
    load nnBS_TestData.mat;         % Load prerecorded test samples
else

Data Generation Parameters

Configure the scenario following the default values in TR 38.843 Table 6.3.1-1.

    prm.NCellID               = 1;
    prm.FrequencyRange        = 'FR2';
    prm.Scenario              = "UMa";

    prm.CenterFrequency       = 30e9; % Hz
    prm.SSBlockPattern        = "Case D"; % Case A/B/C/D/E

    % Number of transmitted blocks. Set it to empty to let the example use
    % the minimum number that ensures a full coverage of the 120-degree
    % sector without overlapping of beams or gaps in the coverage
    prm.NumSSBlocks           = [];

    prm.InterSiteDistance     = 200; % meters
    prm.PowerBSs              = 40; % dBm
    prm.UENoiseFigure         = 10; % UE receiver noise figure in dB

    % Define the method to compute the RSRP: |SSSonly| uses SSS alone and
    % |SSSwDMRS| uses SSS and PBCH DM-RS.
    prm.RSRPMode              = 'SSSwDMRS';

Antenna Array Configuration

    c = physconst('LightSpeed');        % Propagation speed
    prm.Lambda = c/prm.CenterFrequency; % Wavelength
    prm.ElevationSweep = false;         % Enable/disable elevation sweep

Define the transmit antenna array as a rectangular array with 4-by-8 cross-polarized elements, as defined in TR 38.901. The example considers the base station covering the first of a three-sector cell, as defined in TR 38.901 Table 7.8-1, where the first sector is centered at 30 degrees. Set the antenna sweep limits in azimuth to cover the entire 120-degree sector, considering that the antenna array points towards the center of the sector.

    % Transmit array
    prm.TransmitAntennaArray = phased.NRRectangularPanelArray(...
        Size=[4,8,1,1],...
        Spacing=[0.5,0.5,1,1]*prm.Lambda);

    % Transmit azimuth and elevation sweep limits in degrees
    prm.TxAZlim = [-60 60];
    prm.TxELlim = [-90 0];

Define the transmit antenna downtilt angle in degrees. The default value is defined in TR 38.843 Table 6.3.1-2.

    prm.TxDowntilt = 110;

Define the receive antenna array as a rectangular array with 1-by-4 omnidirectional cross-polarized elements, as defined in TR 38.901. Set the antenna sweep limits in azimuth to cover half of the entire 360-degree space, as the antenna array pattern is symmetrical and antenna elements are omnidirectional.

    % Receive array
    prm.ReceiveAntennaArray = phased.NRRectangularPanelArray(...
        Size=[1,4,1,1],...
        Spacing=[0.5,0.5,1,1]*prm.Lambda,...
        ElementSet={phased.ShortDipoleAntennaElement,...
        phased.ShortDipoleAntennaElement});
    % Ensure the two elements are cross polarized with +45 and -45 deg
    % polarization angles
    prm.ReceiveAntennaArray.ElementSet{1}.AxisDirection = "Custom";
    prm.ReceiveAntennaArray.ElementSet{1}.CustomAxisDirection = [0;  1; 1];
    prm.ReceiveAntennaArray.ElementSet{2}.AxisDirection = "Custom";
    prm.ReceiveAntennaArray.ElementSet{2}.CustomAxisDirection = [0; -1; 1];

    % Receive azimuth and elevation sweep limits in degrees
    prm.RxAZlim = [-90 90];
    prm.RxELlim = [0 90];

Validate the current parameter set.

    prm = validateParams(prm);

Generate Training Data

Set the number of UE locations for the training data. The hGenData38901Channel function randomly positions the specified number of UEs within the first sector boundaries of the cell.

    prmTrain = prm;
    prmTrain.NumUELocations = 15e3;
    prmTrain.Seed = 42; % Set random number generator seed for repeatability

Generate the training data for each UE location.

    disp("Generating training data...")
    [optBeamPairIdxTrain,rsrpMatTrain,dataTrain] = hGenData38901Channel(prmTrain);
    disp("Finished generating training data.")

Generate Testing Data

Set the number of UE locations for the testing data.

    prmTest = prm;
    prmTest.NumUELocations = 500;
    prmTest.Seed = 24; % Set random number generator seed for repeatability

Generate the testing data for each UE location.

    disp("Generating test data...")
    [optBeamPairIdxTest,rsrpMatTest,dataTest] = hGenData38901Channel(prmTest);
    disp("Finished generating test data.")

Save generated data.

    if saveData
        save('nnBS_prm.mat','prm');
        save('nnBS_TrainingData.mat','optBeamPairIdxTrain','rsrpMatTrain','dataTrain');
        save('nnBS_TestData.mat','optBeamPairIdxTest','rsrpMatTest','dataTest');
    end
end

Plot Transmitter and UE Locations

Plot training and testing data within the first sector of the cell, as defined in TR 38.901.

% Extract the UE and BS positions for training and testing data
positionsUE = {dataTrain.PosUE, dataTest.PosUE};
positionsBS = {dataTrain.PosBS, dataTest.PosBS};
plotLocations(positionsUE, positionsBS, prm.InterSiteDistance);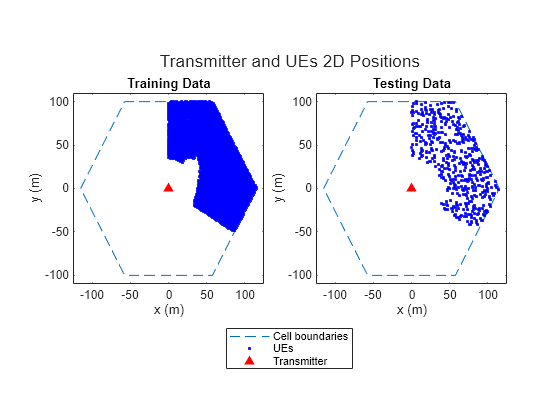

Data Processing and Visualization

Augment the categorical data so that the number of classes matches the possible number of beam pairs (although classes may have unequal number of elements). The augmentation is to ensure that the output of the neural network has the desired dimension.

Process Training Data

NumBeamPairs = prm.NumRxBeams*prm.NumTxBeams;
allBeamPairIdxCell = cellstr(string((1:NumBeamPairs)'));

% Create the categories from the optimal beam index data
optBeamPairIdxCellTrain = cellstr(string(optBeamPairIdxTrain));

% Augment the categories to be as many as the total number of beam pairs
optBeamPairIdxCellTrain = categorical(optBeamPairIdxCellTrain, allBeamPairIdxCell);

Process Testing Data

% Create the categories from the optimal beam index data
optBeamPairIdxCellTest = cellstr(string(optBeamPairIdxTest));

% Augment the categories to be as many as the total number of beam pairs
optBeamPairIdxCellTest = categorical(optBeamPairIdxCellTest, allBeamPairIdxCell);

Create Input/Output Data for Neural Network

% Use 10% of training data as validation data
valTrainDataLen = dataTrain.NumUELocations;
valDataLen = round(0.1*valTrainDataLen);
trainDataLen = valTrainDataLen-valDataLen;

% Randomly shuffle the training data such that the distribution of the
% extracted validation data is closer to the training data
rng(111)
shuffledIdx = randperm(dataTrain.NumUELocations);
optBeamPairIdxCellTrain = optBeamPairIdxCellTrain(shuffledIdx);
optBeamPairIdxTrain = optBeamPairIdxTrain(shuffledIdx);
rsrpMatTrain = rsrpMatTrain(:,:,shuffledIdx);
sampledLocMatTrain = dataTrain.PosUE(shuffledIdx, :);

% Create training input/output data
trainInput = sampledLocMatTrain(valDataLen+1:end, :);
trainOut = optBeamPairIdxCellTrain(valDataLen+1:end);

% Create validation input/output data
valInput = sampledLocMatTrain(1:valDataLen, :);
valOut = optBeamPairIdxCellTrain(1:valDataLen);

% Create test input/output data
testDataLen = dataTest.NumUELocations;
testInput = dataTest.PosUE;
testOut = optBeamPairIdxCellTest;

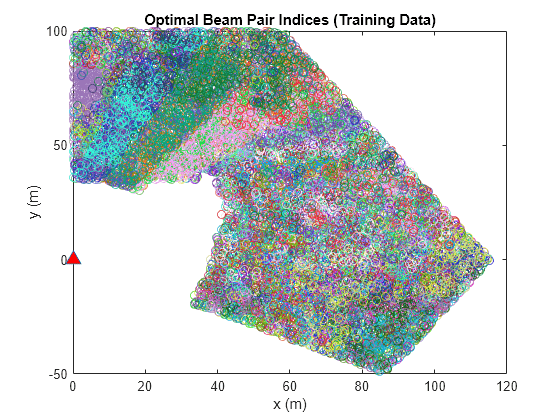
Plot Optimal Beam Pair Distribution for Training Data

Plot the location and the optimal beam pair for each training sample. Each color represents one beam pair index. Data points of the same color belong to the same class. To include each beam pair value, increase the training data set. The plot indicates the decision regions for the generated dataset used to train a classification neural network.

plotBeamPairsDist(sampledLocMatTrain,optBeamPairIdxTrain,dataTrain.PosBS,NumBeamPairs);

Figure contains an axes object. The axes object with title Optimal Beam Pair Indices (Training Data), xlabel x (m), ylabel y (m) contains 71 objects of type line. One or more of the lines displays its values using only markers

Optimal Beam Pair Histogram

Plot a histogram that shows how many times each beam pair is optimal. If some beam pairs are never optimal, try increasing the training and testing dataset by increasing the number of UE locations.

data = {trainOut, valOut, testOut};
plotBeamPairsHist(data,NumBeamPairs);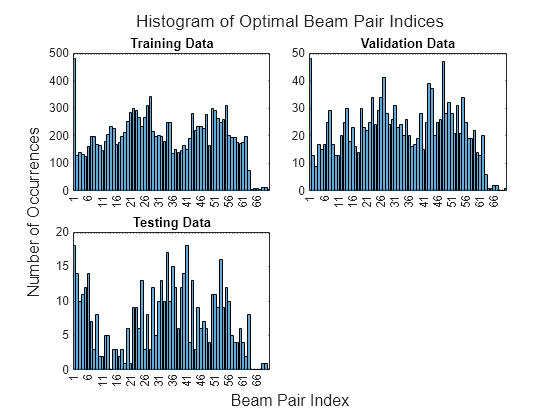

Figure contains 3 axes objects. Axes object 1 with title Training Data contains an object of type categoricalhistogram. Axes object 2 with title Validation Data contains an object of type categoricalhistogram. Axes object 3 with title Testing Data contains an object of type categoricalhistogram.

Design and Train Neural Network

Train a neural network with four hidden layers [5]. To enable training, select the doTraining checkbox.

This example weights the classes in the training data set. Classes that occur more frequently have smaller weights and classes that occur less frequently have larger weights. You can avoid weighting the classes by deselecting the useDiffClassWeights checkbox.

Modify the network to experiment with different designs. If you modify one of the provided data sets, you must retrain the network with the modified data sets. To use the trained network in subsequent runs, select the saveNet checkbox.

doTraining          = false;
useDiffClassWeights = true;
saveNet             = false;

if doTraining
    if useDiffClassWeights
        catCount = countcats(trainOut);
        catFreq = catCount/length(trainOut);
        nnzIdx = (catFreq ~= 0);
        medianCount = median(catFreq(nnzIdx));
        classWeights = 10*ones(size(catFreq));
        classWeights(nnzIdx) = medianCount./catFreq(nnzIdx);
        filename = 'nnBS_trainedNetwWeighting.mat';
    else
        classWeights = ones(1,NumBeamPairs);
        filename = 'nnBS_trainedNet.mat';
    end

    % Neural network design
    layers = [ ...
        featureInputLayer(3,'Name','input','Normalization','rescale-zero-one')

        fullyConnectedLayer(96,'Name','linear1')
        leakyReluLayer(0.01,'Name','leakyRelu1')

        fullyConnectedLayer(96,'Name','linear2')
        leakyReluLayer(0.01,'Name','leakyRelu2')

        fullyConnectedLayer(96,'Name','linear3')
        leakyReluLayer(0.01,'Name','leakyRelu3')

        fullyConnectedLayer(96,'Name','linear4')
        leakyReluLayer(0.01,'Name','leakyRelu4')

        fullyConnectedLayer(NumBeamPairs,'Name','linear5')
        softmaxLayer('Name','softmax')];

Set the maxEpochs to 50 and InitialLearnRate to 1e-4 to avoid overfitting the network to the training data. Use accuracyMetric (Deep Learning Toolbox) object and set NumTopKClasses to 30 to plot the Top-30 beams accuracy while training.

    maxEpochs = 50;
    miniBatchSize = 500;

    options = trainingOptions("adam", ...
        MaxEpochs=maxEpochs, ...
        MiniBatchSize=miniBatchSize, ...
        InitialLearnRate=1e-4, ...
        ValidationData={valInput,valOut}, ...
        ValidationFrequency=500, ...
        OutputNetwork="best-validation-loss", ...
        Shuffle="every-epoch", ...
        Plots="training-progress", ...
        Verbose=false, ...
        Metric=accuracyMetric(Name="Top30_Accuracy",NumTopKClasses=30));

    % Train the network
    net = trainnet(trainInput,trainOut,layers, ...
        @(x,t) crossentropy(x,t,classWeights,WeightsFormat='C'),options);

    if saveNet
        save(filename,'net');
    end
else
    if useDiffClassWeights
        load 'nnBS_trainedNetwWeighting.mat';
    else
        load 'nnBS_trainedNet.mat';
    end
end

The network reaches a 90% accuracy for the top-30 beam pairs after 50 epochs.

Compare Different Approaches: Top-K Accuracy

This section tests the trained network with unseen test data considering the top-K accuracy metric. The top-K accuracy metric has been widely used in the neural network-based beam selection task.

Given a receiver location, the neural network first outputs $K$ recommended beam pairs. Then it performs an exhaustive sequential search on these $K$ beam pairs and selects the one with the highest average RSRP as the final prediction. If the true optimal beam pair is the final selected beam pair, then a successful prediction occurs. Equivalently, a success occurs when the true optimal beam pair is one of the $K$ recommended beam pairs by the neural network.

To use as benchmarks, the example implements three other methods to find the optimal beam pair indices. Each method produces the $K$ recommended beam pairs.

KNN - For a test sample, this method first collects $K$ closest training samples based on GPS coordinates. The method then recommends all the beam pairs associated with these $K$ training samples. Since each training sample has a corresponding optimal beam pair, the number of beam pairs recommended is at most $K$ (some beam pairs might be the same).
Statistical Info [7] - This method first ranks all the beam pairs according to their relative frequency in the testing set, and then always selects the first $K$ beam pairs.
Random [7] - For a test sample, this method randomly chooses $K$ beam pairs.

The plot shows that for $K = 30$ , the accuracy is already more than 90%, which highlights the effectiveness of using the trained neural network for the beam selection task. When $K = 70$ , the Statistical Info scheme becomes an exhaustive search over all the 70 beam pairs. Hence the Statistical Info scheme achieves an accuracy of 100%. However, when $K = 70,$ KNN considers 70 closest training samples, and the number of distinct beam pairs from these samples is often less than 70. Hence, KNN does not achieve an accuracy of 100%.

rng(111)    % for repeatability of the "Random" policy
statisticCount = countcats(testOut);
predTestOutput = predict(net,testInput);

K = NumBeamPairs;
accNeural = zeros(1,K);
accKNN = zeros(1,K);
accStatistic = zeros(1,K);
accRandom = zeros(1,K);
for k = 1:K
    predCorrectNeural = zeros(testDataLen,1);
    predCorrectKNN = zeros(testDataLen,1);
    predCorrectStats = zeros(testDataLen,1);
    predCorrectRandom = zeros(testDataLen,1);
    knnIdx = knnsearch(trainInput,testInput,'K',k);

    for n = 1:testDataLen
        trueOptBeamIdx = double(testOut(n));

        % Neural Network
        [~, topKPredOptBeamIdx] = maxk(predTestOutput(n, :),k);
        if any(topKPredOptBeamIdx == trueOptBeamIdx)
            % if true, then the true correct index belongs to one of the K predicted indices
            predCorrectNeural(n,1) = 1;
        end

        % KNN
        neighborsIdxInTrainData = knnIdx(n,:);
        topKPredOptBeamIdx= optBeamPairIdxTrain(neighborsIdxInTrainData);
        if any(topKPredOptBeamIdx == trueOptBeamIdx)
            % if true, then the true correct index belongs to one of the K predicted indices
            predCorrectKNN(n,1) = 1;
        end

        % Statistical Info
        [~, topKPredOptBeamIdx] = maxk(statisticCount,k);
        if any(topKPredOptBeamIdx == trueOptBeamIdx)
            % if true, then the true correct index belongs to one of the K predicted indices
            predCorrectStats(n,1) = 1;
        end

        % Random
        topKPredOptBeamIdx = randperm(NumBeamPairs,k);
        if sum(topKPredOptBeamIdx == trueOptBeamIdx) > 0
            % if true, then the true correct index belongs to one of the K predicted indices
            predCorrectRandom(n,1) = 1;
        end

    end

    accNeural(k)    = sum(predCorrectNeural)/testDataLen*100;
    accKNN(k)       = sum(predCorrectKNN)/testDataLen*100;
    accStatistic(k) = sum(predCorrectStats)/testDataLen*100;
    accRandom(k)    = sum(predCorrectRandom)/testDataLen*100;

end

Plot the results.

results = {accNeural, accKNN, accStatistic, accRandom};
plotResults(results,K);
ylabel("Top-$K$ Accuracy (\%)",Interpreter="latex");
legend("Neural Network","KNN","Statistical Info","Random",Location="best");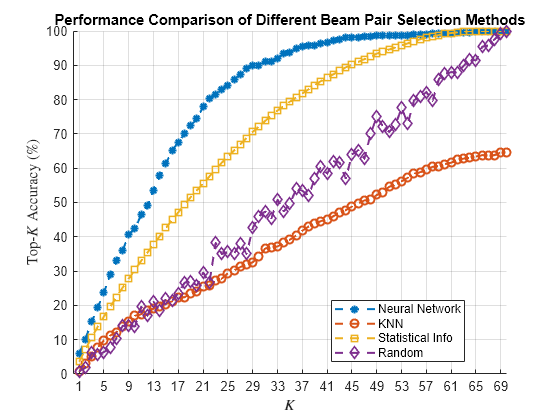

$Figure contains an axes object. The axes object with title Performance Comparison of Different Beam Pair Selection Methods, xlabel $K$, ylabel Top-$K$ blank Accuracy blank (\%) contains 4 objects of type line. These objects represent Neural Network, KNN, Statistical Info, Random.$

Compare Different Approaches: Average RSRP

Using unseen test data, compute the average RSRP achieved by the neural network and the three benchmarks.

rng(111)    % for repeatability of the "Random" policy
K = NumBeamPairs;
rsrpOptimal = zeros(1,K);
rsrpNeural = zeros(1,K);
rsrpKNN = zeros(1,K);
rsrpStatistic = zeros(1,K);
rsrpRandom = zeros(1,K);
for k = 1:K
    rsrpSumOpt = 0;
    rsrpSumNeural = 0;
    rsrpSumKNN = 0;
    rsrpSumStatistic = 0;
    rsrpSumRandom = 0;

    knnIdx = knnsearch(trainInput,testInput,'K',k);

    for n = 1:testDataLen
        % Exhaustive Search
        trueOptBeamIdx = testOut(n);
        rsrp = rsrpMatTest(:,:,n);
        if ~isinf(rsrp(trueOptBeamIdx))
            rsrpSumOpt = rsrpSumOpt + rsrp(trueOptBeamIdx);
        end

        % Neural Network
        [~, topKPredOptCatIdx] = maxk(predTestOutput(n, :),k);
        if ~isinf(max(rsrp(topKPredOptCatIdx)))
            rsrpSumNeural = rsrpSumNeural + max(rsrp(topKPredOptCatIdx));
        end

        % KNN
        neighborsIdxInTrainData = knnIdx(n,:);
        topKPredOptBeamIdxKNN = optBeamPairIdxTrain(neighborsIdxInTrainData);
        if ~isinf(max(rsrp(topKPredOptBeamIdxKNN)))
            rsrpSumKNN = rsrpSumKNN + max(rsrp(topKPredOptBeamIdxKNN));
        end

        % Statistical Info
        [~, topKPredOptCatIdxStat] = maxk(statisticCount,k);
        if ~isinf(max(rsrp(topKPredOptCatIdxStat)))
            rsrpSumStatistic = rsrpSumStatistic + max(rsrp(topKPredOptCatIdxStat));
        end

        % Random
        topKPredOptBeamIdxRand = randperm(NumBeamPairs,k);
        if ~isinf(max(rsrp(topKPredOptBeamIdxRand)))
            rsrpSumRandom = rsrpSumRandom + max(rsrp(topKPredOptBeamIdxRand));
        end
    end
    rsrpOptimal(k)  = rsrpSumOpt/testDataLen;
    rsrpNeural(k)   = rsrpSumNeural/testDataLen;
    rsrpKNN(k)      = rsrpSumKNN/testDataLen;
    rsrpStatistic(k) = rsrpSumStatistic/testDataLen;
    rsrpRandom(k)   = rsrpSumRandom/testDataLen;
end

Plot the results.

results = {rsrpNeural, rsrpKNN, rsrpStatistic, rsrpRandom, rsrpOptimal};
plotResults(results,K);
ylabel("Average RSRP");
legend("Neural Network","KNN","Statistical Info","Random","Exhaustive Search",Location="best");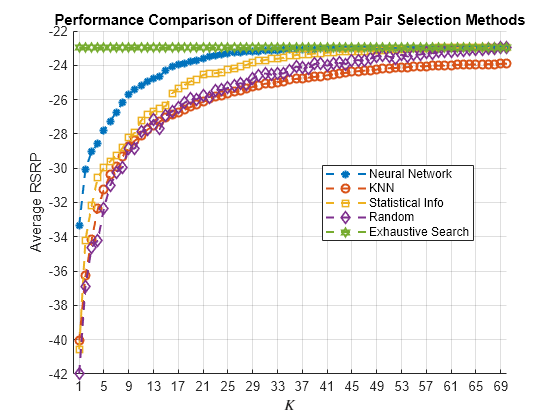

Figure contains an axes object. The axes object with title Performance Comparison of Different Beam Pair Selection Methods, xlabel $K$, ylabel Average RSRP contains 5 objects of type line. These objects represent Neural Network, KNN, Statistical Info, Random, Exhaustive Search.

Compare the end values for the optimal, neural network, and KNN approaches.

table(rsrpOptimal(end-3:end)', rsrpNeural(end-3:end)', rsrpKNN(end-3:end)', VariableNames=["Optimal","Neural Network","KNN"])

ans=4×3 table
    Optimal    Neural Network      KNN  
    _______    ______________    _______

    -22.975       -22.978        -23.934
    -22.975       -22.978        -23.931
    -22.975       -22.975         -23.92
    -22.975       -22.975        -23.909

The performance gap between KNN and the optimal methods indicates that the KNN might not perform well even when a larger set of beam pairs is considered, say, 256.

Conclusion and Further Exploration

This example describes the application of a neural network to the beam selection task for a 5G NR system. You can design and train a neural network that outputs a set of $K$ good beam pairs. Beam sweeping overhead can be reduced by an exhaustive search only on those selected $K$ beam pairs.

The example enables you to specify the number of UE locations in the TR 38.901 channel. To see the impact of the channel on the beam selection, experiment with different scenarios, antenna elevation sweeping, and number of transmit and receive beams. The example also provides presaved datasets that can be used to experiment with different network structures and training hyperparameters.

From simulation results, for the prerecorded TR 38.901 channel for 70 beam pairs, the proposed algorithm achieves a top-K accuracy of 90% when $K = 30$ . This result demonstrates that by using the neural network, you can perform the exhaustive search over less than half of all the beam pairs, which reduces the beam sweeping overhead by more than 50%. Experiment with varying other system parameters to see the efficacy of the network by regenerating data, then retraining and retesting the network.

References

3GPP TR 38.802, "Study on New Radio access technology physical layer aspects." 3rd Generation Partnership Project; Technical Specification Group Radio Access Network.
3GPP TR 38.843, "Study on Artificial Intelligence (AI)/Machine Learning (ML) for NR air interface" 3rd Generation Partnership Project; Technical Specification Group Radio Access Network.
3GPP TR 38.901, "Study on channel model for frequencies from 0.5 to 100 GHz" 3rd Generation Partnership Project; Technical Specification Group Radio Access Network.
Klautau, A., González-Prelcic, N., and Heath, R. W., "LIDAR data for deep learning-based mmWave beam-selection," IEEE Wireless Communications Letters, vol. 8, no. 3, pp. 909–912, Jun. 2019.
Heng, Y., and Andrews, J. G., "Machine Learning-Assisted Beam Alignment for mmWave Systems," 2019 IEEE Global Communications Conference (GLOBECOM), 2019, pp. 1-6, doi: 10.1109/GLOBECOM38437.2019.9013296.
Klautau, A., Batista, P., González-Prelcic, N., Wang, Y., and Heath, R. W., "5G MIMO Data for Machine Learning: Application to Beam-Selection Using Deep Learning," 2018 Information Theory and Applications Workshop (ITA), 2018, pp. 1-9, doi: 10.1109/ITA.2018.8503086.
Matteo, Z., <https://github.com/ITU-AI-ML-in-5G-Challenge/PS-012-ML5G-PHY-Beam-Selection_BEAMSOUP> (This is the team achieving the highest test score in the ITU Artificial Intelligence/Machine Learning in 5G Challenge in 2020).
Sim, M. S., Lim, Y., Park, S. H., Dai, L., and Chae, C., "Deep Learning-Based mmWave Beam Selection for 5G NR/6G With Sub-6 GHz Channel Information: Algorithms and Prototype Validation," IEEE Access, vol. 8, pp. 51634-51646, 2020.

Local Function

function prm = validateParams(prm) %#ok<*DEFNU>
    % Validate user specified parameters and return updated parameters
    %
    % Only cross-dependent checks are made for parameter consistency.

    if strcmpi(prm.FrequencyRange,'FR1')
        if prm.CenterFrequency > 7.125e9 || prm.CenterFrequency < 410e6
            error(['Specified center frequency is outside the FR1 ', ...
                'frequency range (410 MHz - 7.125 GHz).']);
        end
        if strcmpi(prm.SSBlockPattern,'Case D') ||  ...
                strcmpi(prm.SSBlockPattern,'Case E')
            error(['Invalid SSBlockPattern for selected FR1 frequency ' ...
                'range. SSBlockPattern must be one of ''Case A'' or ' ...
                '''Case B'' or ''Case C'' for FR1.']);
        end
        if (prm.CenterFrequency <= 3e9) && (length(prm.SSBTransmitted)~=4)
            error(['SSBTransmitted must be a vector of length 4 for ' ...
                'center frequency less than or equal to 3GHz.']);
        end
        if (prm.CenterFrequency > 3e9) && (length(prm.SSBTransmitted)~=8)
            error(['SSBTransmitted must be a vector of length 8 for ', ...
                'center frequency greater than 3GHz and less than ', ...
                'or equal to 7.125GHz.']);
        end
    else % 'FR2'
        if prm.CenterFrequency > 52.6e9 || prm.CenterFrequency < 24.25e9
            error(['Specified center frequency is outside the FR2 ', ...
                'frequency range (24.25 GHz - 52.6 GHz).']);
        end
        if ~(strcmpi(prm.SSBlockPattern,'Case D') || ...
                strcmpi(prm.SSBlockPattern,'Case E'))
            error(['Invalid SSBlockPattern for selected FR2 frequency ' ...
                'range. SSBlockPattern must be either ''Case D'' or ' ...
                '''Case E'' for FR2.']);
        end
    end

    % Verify that there are multiple TX and Rx antennas
    prm.NumTx = getNumElements(prm.TransmitAntennaArray);
    prm.NumRx = getNumElements(prm.ReceiveAntennaArray);
    if prm.NumTx==1 || prm.NumRx==1
        error(['Number of transmit or receive antenna elements must be', ...
            ' greater than 1.']);
    end

    % Number of beams at transmit end
    % Assume a number of beams so that the beams span the entire 120-degree
    % sector, with a maximum of 64 beams, as mentioned in TR 38.843 Table
    % 6.3.1-1
    % Assume the number of transmitted blocks is the same as the number of
    % beams at transmit end
    if prm.FrequencyRange=="FR1"
        maxNumSSBBlocks = 8;
    else % FR2
        maxNumSSBBlocks = 64;
    end
    if isempty(prm.NumSSBlocks)
        % The number of blocks/beams is automatically generated as the
        % minimum need to span the 120-degree sector
        azTxBW = beamwidth(prm.TransmitAntennaArray,prm.CenterFrequency,Cut='Azimuth');
        numAZTxBeams = round(diff(prm.TxAZlim)/azTxBW);

        if prm.ElevationSweep
            % If elevation sweep is enabled, consider elevation as well in
            % the computation of the number of blocks/beams needed.
            elTxBW = beamwidth(prm.TransmitAntennaArray,prm.CenterFrequency,'Cut','Elevation');
            numELTxBeams = round(diff(prm.TxELlim)/elTxBW);
        else
            numELTxBeams = 1;
        end

        prm.NumTxBeams = min(numAZTxBeams*numELTxBeams, maxNumSSBBlocks);
        prm.NumSSBlocks = prm.NumTxBeams;
    else
        % The number of blocks/beams is defined by the user
        if prm.NumSSBlocks>maxNumSSBBlocks
            error("Invalid number of SSB blocks. For " + prm.FrequencyRange + ...
                ", there can be only up to " + maxNumSSBBlocks + " blocks.");
        end
        prm.NumTxBeams = prm.NumSSBlocks;
    end
    prm.SSBTransmitted = [ones(1,prm.NumTxBeams) zeros(1,maxNumSSBBlocks-prm.NumTxBeams)];

    % Number of beams at receive end
    % Assume a number of beams so that the beams cover the full azimuth
    % sweep, with a maximum of 8 beams, as mentioned in TR 38.843 Table
    % 6.3.1-1.
    azRxBW = beamwidth(prm.ReceiveAntennaArray,prm.CenterFrequency,Cut='Azimuth');
    numAZRxBeams = round(diff(prm.RxAZlim)/azRxBW);
    if prm.ElevationSweep
        % If elevation sweep is enabled, consider elevation as well in
        % the computation of the number of blocks/beams needed.
        elRxBW = beamwidth(prm.ReceiveAntennaArray,prm.CenterFrequency,'Cut','Elevation');
        numELRxBeams = round(diff(prm.RxELlim)/elRxBW);
    else
        numELRxBeams = 1;
    end
    prm.NumRxBeams = min(numAZRxBeams*numELRxBeams, 8);

    % Select SCS based on SSBlockPattern
    switch lower(prm.SSBlockPattern)
        case 'case a'
            scs = 15;
            cbw = 10;
            scsCommon = 15;
        case {'case b', 'case c'}
            scs = 30;
            cbw = 25;
            scsCommon = 30;
        case 'case d'
            scs = 120;
            cbw = 100;
            scsCommon = 120;
        case 'case e'
            scs = 240;
            cbw = 200;
            scsCommon = 120;
    end
    prm.SCS = scs;
    prm.ChannelBandwidth = cbw;
    prm.SubcarrierSpacingCommon = scsCommon;

    % Set up SSBurst configuration
    txBurst = nrWavegenSSBurstConfig;
    txBurst.BlockPattern = prm.SSBlockPattern;
    txBurst.TransmittedBlocks = prm.SSBTransmitted;
    txBurst.Period = 20;
    txBurst.SubcarrierSpacingCommon = prm.SubcarrierSpacingCommon;
    prm.TxBurst = txBurst;
end

function plotLocations(positionsUE,positionsBS,ISD)
    % Plot UE and BS 2D locations within the cell boundaries

    % Compute the cell boundaries
    [sitex,sitey] = h38901Channel.sitePolygon(ISD);

    % Plot training and testing data
    t = tiledlayout(TileSpacing="compact", GridSize=[1,2]);
    titles = ["Training Data", "Testing Data"];
    for idx = 1:numel(titles)
        nexttile
        plot(sitex,sitey,'--');
        box on;
        hold on;
        plot(positionsUE{idx}(:,1), positionsUE{idx}(:,2), 'b.');
        plot(positionsBS{idx}(:,1), positionsBS{idx}(:,2), '^', MarkerEdgeColor='r', MarkerFaceColor='r');
        xlabel("x (m)");
        ylabel("y (m)");
        xlim([min(sitex)-10 max(sitex)+10]);
        ylim([min(sitey)-10 max(sitey)+10]);
        axis('square');
        title(titles(idx));
    end
    title(t, "Transmitter and UEs 2D Positions");
    l = legend("Cell boundaries","UEs","Transmitter");
    l.Layout.Tile = "south";
end

function plotBeamPairsDist(sampledLocMat,avgOptBeamPairIdxScalar,PosBS,NumBeamPairs)
    % Plot the optimal beam pair distribution across the UE locations

    figure
    rng(111) % for colors in plot
    color = rand(NumBeamPairs, 3);
    uniqueOptBeamPairIdx = unique(avgOptBeamPairIdxScalar);
    hold on;
    for n = 1:length(uniqueOptBeamPairIdx)
        beamPairIdx = find(avgOptBeamPairIdxScalar == uniqueOptBeamPairIdx(n));
        locX = sampledLocMat(beamPairIdx, 1);
        locY = sampledLocMat(beamPairIdx, 2);
        plot(locX, locY, LineStyle="none", Marker="o", MarkerEdgeColor=color(n, :));
    end
    box on;
    plot(PosBS(:,1), PosBS(:,2), LineStyle="none", Marker="^", MarkerFaceColor="r", MarkerSize=10);
    hold off;
    xlabel("x (m)");
    ylabel("y (m)");
    title("Optimal Beam Pair Indices (Training Data)");
end

function plotBeamPairsHist(data,NumBeamPairs)
    % Plot the optimal beam pair histogram

    t = tiledlayout(TileSpacing="compact", GridSize=[2,2]);
    titles = ["Training Data", "Validation Data", "Testing Data"];
    labelIdx = 1:NumBeamPairs;
    labelIdx(1:5:end) = [];
    labels = cell(1, numel(labelIdx));
    labels(:) = {""};
    for idx = 1:numel(titles)
        ax = nexttile;
        histogram(data{idx});
        ax.XTickLabel(labelIdx) = labels;
        title(titles(idx));
    end
    title(t, "Histogram of Optimal Beam Pair Indices");
    xlabel(t, "Beam Pair Index");
    ylabel(t, "Number of Occurrences");
end

function plotResults(results,K)
    % Plot the results from the comparison of different beam pair selection
    % methods

    figure
    lineWidth = 1.5;
    markerStyle = ["*","o","s","d","h"];
    hold on
    for idx = 1:numel(results)
        plot(1:K,results{idx},LineStyle="--",LineWidth=lineWidth,Marker=markerStyle(idx));
    end
    hold off
    grid on
    xticks(1:4:K)
    xlabel("$K$",Interpreter="latex");
    title("Performance Comparison of Different Beam Pair Selection Methods");
end