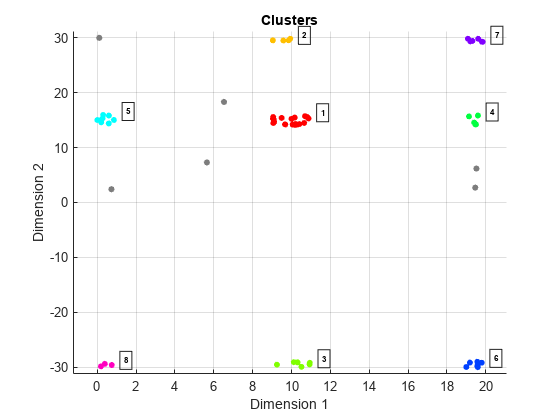
clusterDBSCAN

Density-based algorithm for clustering data

Since R2021a

Description

clusterDBSCAN clusters data points belonging to a P-dimensional feature space using the density-based spatial clustering of applications with noise (DBSCAN) algorithm. The clustering algorithm assigns points that are close to each other in feature space to a single cluster. For example, a radar system can return multiple detections of an extended target that are closely spaced in range, angle, and Doppler. clusterDBSCAN assigns these detections to a single detection.

The DBSCAN algorithm assumes that clusters are dense regions in data space separated by regions of lower density and that all dense regions have similar densities.
To measure density at a point, the algorithm counts the number of data points in a neighborhood of the point. A neighborhood is a P-dimensional ellipse (hyperellipse) in the feature space. The radii of the ellipse are defined by the P-vector ε. ε can be a scalar, in which case, the hyperellipse becomes a hypersphere. Distances between points in feature space are calculated using the Euclidean distance metric. The neighborhood is called an ε-neighborhood. The value of ε is defined by the Epsilon property. Epsilon can either be a scalar or P-vector:
- A vector is used when different dimensions in feature space have different units.
- A scalar applies the same value to all dimensions.
Clustering starts by finding all core points. If a point has a sufficient number of points in its ε-neighborhood, the point is called a core point. The minimum number of points required for a point to become a core point is set by the MinNumPoints property.
The remaining points in the ε-neighborhood of a core point can be core points themselves. If not, they are border points. All points in the ε-neighborhood are called directly density reachable from the core point.
If the ε-neighborhood of a core point contains other core points, the points in the ε-neighborhoods of all the core points merge together to form a union of ε-neighborhoods. This process continues until no more core points can be added.
- All points in the union of ε-neighborhoods are density reachable from the first core point. In fact, all points in the union are density reachable from all core points in the union.
- All points in the union of ε-neighborhoods are also termed density connected even though border points are not necessarily reachable from each other. A cluster is a maximal set of density-connected points and can have an arbitrary shape.
Points that are not core or border points are noise points. They do not belong to any cluster.
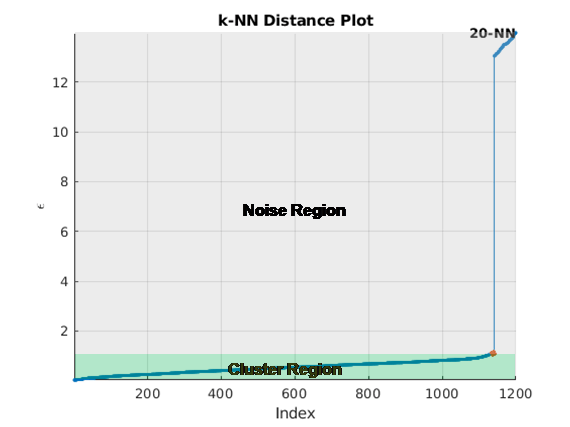
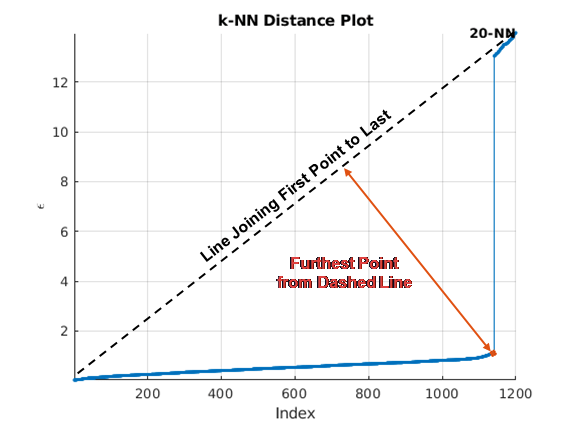
The clusterDBSCAN object can estimate ε using a k-nearest neighbor search, or you can specify values. To let the object estimate ε, set the EpsilonSource property to 'Auto'.
The clusterDBSCAN object can disambiguate data containing ambiguities. Range and Doppler are examples of possibly ambiguous data. Set EnableDisambiguation property to true to disambiguate data.

To cluster detections:

Create the clusterDBSCAN object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

clusterer = clusterDBSCAN

clusterer = clusterDBSCAN(Name,Value)

Description

clusterer = clusterDBSCAN creates a clusterDBSCAN object, clusterer, with default property values.

example

clusterer = clusterDBSCAN(Name,Value) creates a clusterDBSCAN object, clusterer, with each specified Property Name set to the corresponding Value. You can specify additional pairs of arguments in any order as Name1=Value1,...,NameN=ValueN. Any unspecified properties take default values. For example,

clusterer = clusterDBSCAN(MinNumPoints=3,Epsilon=2, ...
EnableDisambiguation=true,AmbiguousDimension=[1 2]);

creates a clusterer object with the EnableDisambiguation property set to true and the AmbiguousDimension set to [1,2].

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

`EpsilonSource` — Source of epsilon
`'Property'` (default) | `'Auto'`

Source of epsilon values defining an ε-neighborhood, specified as 'Property' or 'Auto'.

When you set the EpsilonSource property to 'Property', ε is obtained from the Epsilon property.
When you set the EpsilonSource property to 'Auto', ε is estimated automatically using a k-nearest neighbor (k-NN) search over a range of k values from k_min to k_max.

$\begin{array}{l} k_{\min} = MinNumPoints - 1 \\ k_{\max} = MaxNumPoints - 1 \end{array}$
The subtraction of one is needed because the number of neighbors of a point does not include the point itself, whereas MinNumPoints and MaxNumPoints refer to the total number of points in a neighborhood.

Data Types: char | string

`Epsilon` — Radius for neighborhood search
`10.0` (default) | positive scalar | positive, real-valued 1-by-P row vector

Radius for a neighborhood search, specified as a positive scalar or positive, real-valued 1-by-P row vector. P is the number of features in the input data, X.

Epsilon defines the radii of an ellipse around any point to create an ε-neighborhood. When Epsilon is a scalar, the same radius applies to all feature dimensions. You can apply different epsilon values for different features by specifying a positive, real-valued 1-by-P row vector. A row vector creates a multidimensional ellipse (hyperellipse) search area, useful when the data features have different physical meanings, such as range and Doppler. See Estimate Epsilon for more information about this property.

You can use the clusterDBSCAN.estimateEpsilon or clusterDBSCAN.discoverClusters object functions to help estimate a scalar value for epsilon.

Example: [11 21.0]

Tunable: Yes

Dependencies

To enable this property, set the EpsilonSource property to 'Property'.

Data Types: double

`MinNumPoints` — Minimum number of points required for cluster
`3` (default) | positive integer

The minimum number of points in a cluster, specified as a positive integer. MinNumPoints is the minimum number of points in an ε-neighborhood of a point for that point to become a core point. The purpose of MinNumPoints is to smooth the density estimate. See Choosing the Minimum Number of Points for more information. When the object automatically estimates epsilon using a k-NN search, the starting value of k (k_min) is MinNumPoints - 1.

Example: 5

Data Types: double

`MaxNumPoints` — Set end of k-NN search range
`10` (default) | positive integer

Set end of k-NN search range, specified as a positive integer. When the object automatically estimates epsilon using a k-NN search, the ending value of k (k_max) is MaxNumPoints - 1.

Example: 13

Dependencies

To enable this property, set the EpsilonSource property to 'Auto'.

Data Types: double

`EpsilonHistoryLength` — Length of cluster threshold epsilon history
`10` (default) | positive integer

Length of the stored epsilon history, specified as a positive integer. When set to one, the history is memory-less, meaning that each epsilon estimate is immediately used and no moving-average smoothing occurs. When greater than one, epsilon is averaged over the history length specified.

Example: 5

Dependencies

To enable this property, set the EpsilonSource property to 'Auto'.

Data Types: double

`EnableDisambiguation` — Enable disambiguation of dimensions
`false` (default) | `true`

Switch to enable disambiguation of dimensions, specified as false or true. When true, clustering can occur across boundaries defined by the input amblims at execution. Use the AmbiguousDimensions property to specify the column indices of X in which ambiguities can occur. You can disambiguate up to two dimensions. Turning on disambiguation is not recommended for large data sets.

Data Types: logical

`AmbiguousDimension` — Indices of ambiguous dimensions
`1` (default) | positive integer | 1-by-2 vector of positive integers

Indices of ambiguous dimensions, specified as a positive integer or 1-by-2 vector of positive integers. This property specifies the column of X in which to apply disambiguation. A positive integer indicates a single ambiguous dimension in the input data matrix X. A 1-by-2 row vector specifies two ambiguous dimensions. The size and order of AmbiguousDimension must be consistent with the object input amblims.

Example: [3 4]

Dependencies

To enable this property, set the EnableDisambiguation property to true.

Data Types: double

Usage

Syntax

idx = clusterer(X)

[idx,clusterids] = clusterer(X)

[___] = clusterer(X,amblims)

[___] = clusterer(X,update)

[___] = clusterer(X,amblims,update)

Description

idx = clusterer(X) clusters the points in the input data, X. idx contains a list of IDs identifying the cluster to which each row of X belongs. Noise points are assigned as '–1'.

example

[idx,clusterids] = clusterer(X) also returns an alternate set of cluster IDs, clusterids, for use in the phased.RangeEstimator and phased.DopplerEstimator objects. clusterids assigns a unique ID to each noise point.

example

[___] = clusterer(X,amblims) also specifies the minimum and maximum ambiguity limits, amblims, to apply to the data.

To enable this syntax, set the EnableDisambiguation property to true.

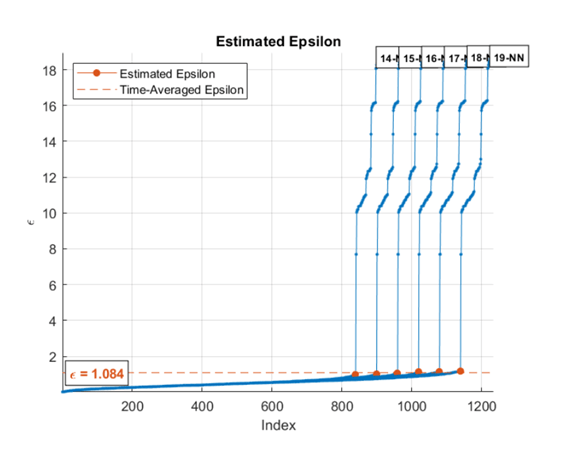
[___] = clusterer(X,update) automatically estimates epsilon from the input data matrix, X, when update is set to true. The estimation uses a k-NN search to create a set of search curves. For more information, see Estimate Epsilon. The estimate is an average of the L most recent Epsilon values where L is specified in EpsilonHistoryLength

To enable this syntax, set the EpsilonSource property to 'Auto', optionally set the MaxNumPoints property, and also optionally set the EpsilonHistoryLength property.

[___] = clusterer(X,amblims,update) sets ambiguity limits and estimates epsilon when update is set to true. To enable this syntax, set EnableDisambiguation to true and set EpsilonSource to 'Auto'.

Input Arguments

expand all

`X` — Input feature data
real-valued N-by-P matrix

Input feature data, specified as a real-valued N-by-P matrix, where N is the number of points and P is the clustering dimension. The N rows correspond to feature points in a P-dimensional feature space. The P columns contain the values of the features over which clustering takes place. The DBSCAN algorithm can cluster any type of data with appropriate MinNumPoints and Epsilon property settings. For example, a two-column input can contain the xy Cartesian coordinates, or range and Doppler.

Data Types: double

`amblims` — Ambiguity limits
1-by-2 real-valued vector (default) | 2-by-2 real-valued matrix

Ambiguity limits, specified as a real-valued 1-by-2 vector or real-valued 2-by-2 matrix. For a single ambiguity dimension, specify the limits as a 1-by-2 vector [MinAmbiguityLimitDimension1,MaxAmbiguityLimitDimension1]. For two ambiguity dimensions, specify the limits as a 2-by-2 matrix [MinAmbiguityLimitDimension1, MaxAmbiguityLimitDimension1; MinAmbiguityLimitDimension2,MaxAmbiguityLimitDimension2]. Ambiguity limits allow clustering across boundaries to ensure that ambiguous detections are appropriately clustered.

The ambiguous columns of X are defined in the AmbiguousDimension property. amblims defines the minimum and maximum ambiguity limits in the same units as the data in the AmbiguousDimension columns of X.

Example: [0 20; -40 40]

Dependencies

To enable this argument, set EnableDisambiguation to true and set the AmbiguousDimension property.

Data Types: double

`update` — Enable automatic update of epsilon
`false` (default) | `true`

Enable automatic update of the epsilon estimate, specified as false or true.

When true, the epsilon threshold is first estimated as the average of the knees of k-NN search curves. The estimate is then added to a buffer whose length L is set in the EpsilonHistoryLength property. The final epsilon that is used is calculated as the average of the L-length epsilon history buffer. If EpsilonHistoryLength is set to 1, the estimate is memory-less. Memory-less means that each epsilon estimate is immediately used and no moving-average smoothing occurs.
When false, a previous epsilon estimate is used. Estimating epsilon is computationally intensive and not recommended for large data sets.

Dependencies

To enable this argument, set the EpsilonSource property to 'Auto' and specify the MaxNumPoints property.

Data Types: double

Output Arguments

expand all

`idx` — Cluster indices
N-by-1 integer-valued column vector

Cluster indices, returned as an integer-valued N-by-1 column vector. idx represents the clustering results of the DBSCAN algorithm. Positive idx values correspond to clusters that satisfy the DBSCAN clustering criteria. A value of '-1' indicates a DBSCAN noise point.

Data Types: double

`clusterids` — Alternative cluster IDs
1-by-N integer-valued row vector

Alternative cluster IDs, returned as a 1-by-N row vector of positive integers. Each value is a unique identifier indicating a hypothetical target cluster. This argument contains unique positive cluster IDs for all points including noise. In contrast, the idx output argument labels noise points with '–1'. Use clusterids as the input to Phased Array System Toolbox™ objects such as phased.RangeEstimator and phased.DopplerEstimator.

Data Types: double

Object Functions

To use an object function, specify the System object™ as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

Specific to `clusterDBSCAN`

`clusterDBSCAN.discoverClusters`	Find cluster hierarchy in data
`clusterDBSCAN.estimateEpsilon`	Estimate neighborhood clustering threshold
`clusterDBSCAN.plot`	Plot clusters

Common to All System Objects

`step`	Run System object algorithm
`release`	Release resources and allow changes to System object property values and input characteristics
`reset`	Reset internal states of System object

Examples

collapse all

Cluster Detections in Range and Doppler

Open Live Script

Create detections of extended objects with measurements in range and Doppler. Assume the maximum unambiguous range is 20 m and the unambiguous Doppler span extends from $- 30$ Hz to $30$ Hz. Data for this example is contained in the dataClusterDBSCAN.mat file. The first column of the data matrix represents range, and the second column represents Doppler.

The input data contains the following extended targets and false alarms:

an unambiguous target located at $(10, 15)$
an ambiguous target in Doppler located at $(10, - 30)$
an ambiguous target in range located at $(20, 15)$
an ambiguous target in range and Doppler located at $(20, 30)$
5 false alarms

Create a clusterDBSCAN object and specify that disambiguation is not performed by setting EnableDisambiguation to false. Solve for the cluster indices.

load('dataClusterDBSCAN.mat');
cluster1 = clusterDBSCAN('MinNumPoints',3,'Epsilon',2, ...
    'EnableDisambiguation',false);
idx = cluster1(x);

Use the clusterDBSCAN plot object function to display the clusters.

plot(cluster1,x,idx)

Figure Clusters contains an axes object. The axes object with title Clusters, xlabel Dimension 1, ylabel Dimension 2 contains 10 objects of type line, scatter, text. One or more of the lines displays its values using only markers

The plot indicates that there are eight apparent clusters and six noise points. The 'Dimension 1' label corresponds to range and the 'Dimension 2' label corresponds to Doppler.

Next, create another clusterDBSCAN object and set EnableDisambiguation to true to specify that clustering is performed across the range and Doppler ambiguity boundaries.

cluster2 = clusterDBSCAN('MinNumPoints',3,'Epsilon',2, ...
    'EnableDisambiguation',true,'AmbiguousDimension',[1 2]);

Perform the clustering using ambiguity limits and then plot the clustering results. The DBSCAN clustering results correctly show four clusters and five noise points. For example, the points at ranges close to zero are clustered with points near 20 m because the maximum unambiguous range is 20 m.

amblims = [0 maxRange; minDoppler maxDoppler];
idx = cluster2(x,amblims);
plot(cluster2,x,idx)

Figure Clusters contains an axes object. The axes object with title Clusters, xlabel Dimension 1, ylabel Dimension 2 contains 6 objects of type line, scatter, text. One or more of the lines displays its values using only markers

Effect of Epsilon on Clustering

Open Live Script

Cluster two-dimensional Cartesian position data using clusterDBSCAN. To illustrate how the choice of epsilon affects clustering, compare the results of clustering with Epsilon set to 1 and Epsilon set to 3.

Create random target position data in xy Cartesian coordinates.

x = [rand(20,2)+12; rand(20,2)+10; rand(20,2)+15];
plot(x(:,1),x(:,2),'.')

Figure contains an axes object. The axes contains a line object which displays its values using only markers.

Create a clusterDBSCAN object with the Epsilon property set to 1 and the MinNumPoints property set to 3.

clusterer = clusterDBSCAN('Epsilon',1,'MinNumPoints',3);

Cluster the data when Epsilon equals 1.

idxEpsilon1 = clusterer(x);

Cluster the data again but with Epsilon set to 3. You can change the value of Epsilon because it is a tunable property.

clusterer.Epsilon = 3;
idxEpsilon2 = clusterer(x);

Plot the clustering results side-by-side. Do this by passing in the axes handles and titles into the plot method. The plot shows that for Epsilon set to 1, three clusters appear. When Epsilon is 3, the two lower clusters are merged into one.

hAx1 = subplot(1,2,1);
plot(clusterer,x,idxEpsilon1, ...
    'Parent',hAx1,'Title','Epsilon = 1')
hAx2 = subplot(1,2,2);
plot(clusterer,x,idxEpsilon2, ...
    'Parent',hAx2,'Title','Epsilon = 3')

Figure contains 2 axes objects. Axes object 1 with title Epsilon = 1, xlabel Dimension 1, ylabel Dimension 2 contains 4 objects of type scatter, text. Axes object 2 with title Epsilon = 3, xlabel Dimension 1, ylabel Dimension 2 contains 3 objects of type scatter, text.

Algorithms

expand all

Clustering Algorithm

Clustering Overview

This section illustrates the basic principles of cluster formation. The figure shows points in a two-dimensional feature space. The clusters are compact and well-separated. A few noise points appear.

Clusters Formed from a Single ε-Neighborhood

Clusters start from core points. The first step in the algorithm is identifying all core points.
The figure here shows the point P₁ and its ε-neighborhood N_ε(P₁). The ε-neighborhood has eight points (including itself) within a radius ε. Using the MinNumPoints property to set the threshold to 8 means that P₁ is a core point. The blue points that lie within N_ε are called border points. These border points are directly density reachable from the core point P₁.
No other points in the figure have enough neighboring points in their ε-neighborhood to become a core point. P₂ is not a core point because it has only five points within its neighborhood. P₂ is directly density reachable from P₁. The reverse is not true because P₂ is not a core point. The one-way arrow connecting the two points shows this asymmetry.
Points that fall outside N_ε(P₁) are noise points (red) and do not belong to the cluster.
Because no other points are core points, the core point and border points are a maximal set of density-connected points and therefore form a cluster.

Cluster of Points from Two ε-Neighborhoods

The next figure shows a larger set of points containing two core points, P₁ and P₂. P₂ is a border point of P₁ but P₂ also has enough points in its own neighborhood to become a core point. Because they are both core points, P₁ is directly density reachable from P₂, and P₁ is directly density reachable from P₂. The two-way arrow connecting them shows this symmetry.
P₃ is directly density reachable from P₂ but not from P₁ (as indicated by the one-way arrow). However, P₃ is called simply density reachable from P₁.
Because no other points are core points, the two core points and their border points form a maximal set of density-connected points and form one cluster.

Cluster Points in Adjacent ε-Neighborhoods

This process of growing a cluster can be extended from core point to core point until there are no more core points to add. The core points and the border points belong to the same cluster. In general, a point P_n is density reachable from point P₁ when there is a chain of core points, P₁,P₂, P₃, …, P_n-1 such that each core point P_i₊₁ is directly density reachable from P_i, and P_n is directly density reachable from P_n_-1.

Density Connectivity

The next figure illustrates some properties of density connectivity.

A cluster can have multiple branching chains, for example (P₁, P₂, P₃, P₄) and (P₁, P₂, P₅, P₆).
Two points, P₆ and P₄, are density connected when there is a third point P₂ such that P₆ and P₄ are density reachable from P₂.
Two density connected points are not necessarily density reachable from one another.
A maximal set of density connected points define a cluster. It does not matter which core point is the starting core point.
All points in a cluster are density reachable from all core points.

Estimate Epsilon

DBSCAN clustering requires a value for the neighborhood size parameter ε. The clusterDBSCAN object and the clusterDBSCAN.estimateEpsilon function use a k-nearest-neighbor search to estimate a scalar epsilon. Let D be the distance of any point P to its k^th nearest neighbor. Define a D_k(P)-neighborhood as a neighborhood surrounding P that contains its k-nearest neighbors. There are k + 1 points in the D_k(P)-neighborhood including the point P itself. An outline of the estimation algorithm is:

For each point, find all the points in its D_k(P)-neighborhood
Accumulate the distances in all D_k(P)-neighborhoods for all points into a single vector.
Sort the vector by increasing distance.
Plot the sorted k-dist graph, which is the sorted distance against point number.
Find the knee of the curve. The value of the distance at that point is an estimate of epsilon.

The figure here shows distance plotted against point index for k = 20. The knee occurs at approximately 1.5. Any points below this threshold belong to a cluster. Any points above this value are noise.

There are several methods to find the knee of the curve. clusterDBSCAN and clusterDBSCAN.estimateEpsilon first define the line connecting the first and last points of the curve. The ordinate of the point on the sorted k-dist graph furthest from the line and perpendicular to the line defines epsilon.

When you specify a range of k values, the algorithm averages the estimate epsilon values for all curves. This figure shows that epsilon is fairly insensitive to k for k ranging from 14 through 19.

To create a single k-NN distance graph, set the MinNumPoints property equal to the MaxNumPoints property.

Choosing the Minimum Number of Points

The purpose of MinNumPoints is to smooth the density estimates. Because a cluster is a maximal set of density-connected points, choose smaller values when the expected number of detections in a cluster is unknown. However, smaller values make the DBSCAN algorithm more susceptible to noise. A general guideline for choosing MinNumPoints is:

Generally, set MinNumPoints = 2P where P is the number of feature dimensions in X.
For data sets that have one or more of the following properties:
- many noise points
- large number of points, N
- large dimensionality, P
- many duplicates
increasing MinNumPoints can often improve clustering results.

Ambiguous Data

The clustering algorithm is general enough to process ambiguities in any feature, but applying clustering to range and Doppler ambiguities in radar are important applications.

Range Ambiguity

The time delay between pulse transmission and reception determines the range, R, of a target. R is proportional to time delay, t, by

$R = \frac{c t}{2}$

where c is the speed of light. Time is measured from the transmission time of the pulse. If only one pulse is transmitted, the equation accurately determines the range.

Often, the radar transmits multiple pulses spaced at intervals T, the pulse repetition interval (PRI). Range ambiguities occur when the echoes from one pulse are not received before the next pulse is transmitted. Range is computed from the time difference of the arrival of the received pulse from the transmission time of the most recent transmitted pulse. Therefore the range can be incorrect by some integer multiple of the unambiguous range. The unambiguous range of a radar system is the maximum range at which a target can be located to guarantee that the reflected pulse from that target corresponds to the most recent transmitted pulse. The PRI determines the unambiguous range.

$R_{\max} = \frac{c T}{2}$

The range of a detection less than R_max is an unambiguous range. Range disambiguation clusters detections that cross ambiguous range boundaries.

Turn on disambiguation by setting the EnableDisambiguation to true. Then, use the AmbiguousDimension property to select the column in the input data corresponding to range. Set the actual ambiguity limits for range using the amblims argument at execution time.

Doppler Ambiguity

Doppler aliasing occurs when echoes arrive from targets that move fast enough for the Doppler frequency to exceed the pulse repetition frequency (PRF). If the Doppler shift is greater than ½ PRF or less than –½ PRF, the Doppler shift is aliased into the range (–½ PRF, ½ PRF). This range is called the unambiguous Doppler. Turn on disambiguation by setting the EnableDisambiguation to true. Then, use the AmbiguousDimension property to select the column in the input data corresponding to Doppler. Set the actual ambiguity limits for Doppler using the amblims argument at execution time. Doppler ambiguity implies radial speed ambiguity as well. Make sure that amblims matches the interpretation of the feature.

References

[1] Ester M., Kriegel H.-P., Sander J., and Xu X. "A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise". Proc. 2nd Int. Conf. on Knowledge Discovery and Data Mining, Portland, OR, AAAI Press, 1996, pp. 226-231.

[2] Erich Schubert, Jörg Sander, Martin Ester, Hans-Peter Kriegel, and Xiaowei Xu. 2017. "DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN". ACM Trans. Database Syst. 42, 3, Article 19 (July 2017), 21 pages.

[3] Dominik Kellner, Jens Klappstein and Klaus Dietmayer, "Grid-Based DBSCAN for Clustering Extended Objects in Radar Data", 2012 IEEE Intelligent Vehicles Symposium.

[4] Thomas Wagner, Reinhard Feger, and Andreas Stelzer, "A Fast Grid-Based Clustering Algorithm for Range/Doppler/DoA Measurements", Proceedings of the 13th European Radar Conference.

[5] Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel, Jörg Sander, "OPTICS: Ordering Points To Identify the Clustering Structure", Proc. ACM SIGMOD’99 Int. Conf. on Management of Data, Philadelphia PA, 1999.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2021a

clusterDBSCAN

Description

Creation

Syntax

Description

Properties

EpsilonSource — Source of epsilon 'Property' (default) | 'Auto'

Epsilon — Radius for neighborhood search 10.0 (default) | positive scalar | positive, real-valued 1-by-P row vector

Dependencies

MinNumPoints — Minimum number of points required for cluster 3 (default) | positive integer

MaxNumPoints — Set end of k-NN search range 10 (default) | positive integer

Dependencies

EpsilonHistoryLength — Length of cluster threshold epsilon history 10 (default) | positive integer

Dependencies

EnableDisambiguation — Enable disambiguation of dimensions false (default) | true

AmbiguousDimension — Indices of ambiguous dimensions 1 (default) | positive integer | 1-by-2 vector of positive integers

Dependencies

Usage

Syntax

Description

Input Arguments

X — Input feature data real-valued N-by-P matrix

amblims — Ambiguity limits 1-by-2 real-valued vector (default) | 2-by-2 real-valued matrix

Dependencies

update — Enable automatic update of epsilon false (default) | true

Dependencies

Output Arguments

idx — Cluster indices N-by-1 integer-valued column vector

clusterids — Alternative cluster IDs 1-by-N integer-valued row vector

Object Functions

Specific to clusterDBSCAN

Common to All System Objects

Examples

Cluster Detections in Range and Doppler

Effect of Epsilon on Clustering

Algorithms

Clustering Algorithm

Estimate Epsilon

Choosing the Minimum Number of Points

Ambiguous Data

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Version History

See Also

`EpsilonSource` — Source of epsilon
`'Property'` (default) | `'Auto'`

`Epsilon` — Radius for neighborhood search
`10.0` (default) | positive scalar | positive, real-valued 1-by-P row vector

`MinNumPoints` — Minimum number of points required for cluster
`3` (default) | positive integer

`MaxNumPoints` — Set end of k-NN search range
`10` (default) | positive integer

`EpsilonHistoryLength` — Length of cluster threshold epsilon history
`10` (default) | positive integer

`EnableDisambiguation` — Enable disambiguation of dimensions
`false` (default) | `true`

`AmbiguousDimension` — Indices of ambiguous dimensions
`1` (default) | positive integer | 1-by-2 vector of positive integers

`X` — Input feature data
real-valued N-by-P matrix

`amblims` — Ambiguity limits
1-by-2 real-valued vector (default) | 2-by-2 real-valued matrix

`update` — Enable automatic update of epsilon
`false` (default) | `true`

`idx` — Cluster indices
N-by-1 integer-valued column vector

`clusterids` — Alternative cluster IDs
1-by-N integer-valued row vector

Specific to `clusterDBSCAN`

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.