Main Content

clusterDBSCAN.estimateEpsilon

Estimate neighborhood clustering threshold

Since R2021a

collapse all in page

Syntax

epsilon = clusterDBSCAN.estimateEpsilon(X,MinNumPoints,MaxNumPoints)
clusterDBSCAN.estimateEpsilon(X,MinNumPoints,MaxNumPoints)

Description

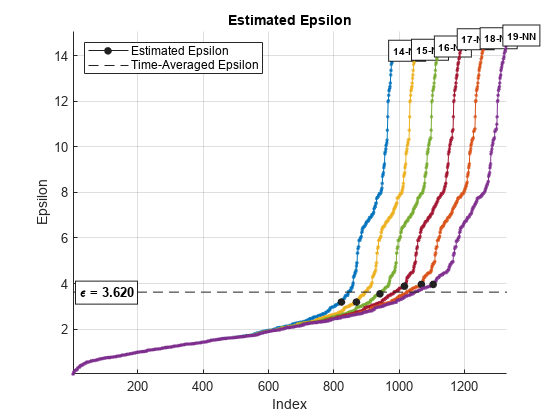
epsilon = clusterDBSCAN.estimateEpsilon(X,MinNumPoints,MaxNumPoints) returns an estimate of the neighborhood clustering threshold, epsilon, used in the density-based spatial clustering of applications with noise (DBSCAN) algorithm. epsilon is computed from input data X using a k-nearest neighbor (k-NN) search. MinNumPoints and MaxNumPoints set a range of k-values for which epsilon is calculated. The range extends from MinNumPoints – 1 through MaxNumPoints – 1. k is the number of neighbors of a point, which is one less than the number of points in a neighborhood.

example

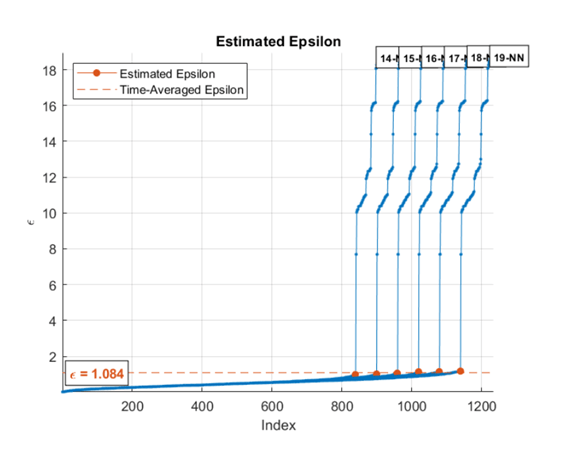
clusterDBSCAN.estimateEpsilon(X,MinNumPoints,MaxNumPoints) displays a figure showing the k-NN search curves and the estimated epsilon. The neighborhood clustering threshold, epsilon, is used in the density-based spatial clustering of applications with noise (DBSCAN) algorithm. epsilon is computed from input data X using a k-nearest neighbor (k-NN) search. MinNumPoints and MaxNumPoints set a range of k-values for which epsilon is calculated. The range extends from MinNumPoints – 1 through MaxNumPoints – 1. k is the number of neighbors of a point, which is one less than the number of points in a neighborhood.

example

Examples

collapse all

Open Live Script

Create simulated target data and use the clusterDBSCAN.estimateEpsilon function to calculate an appropriate epsilon threshold.

Create the target data as xy Cartesian coordinates.

X = [randn(20,2) + [11.5,11.5]; randn(20,2) + [25,15]; ...
    randn(20,2) + [8,20]; 10*rand(10,2) + [20,20]];

Set the range of values for the k-NN search.

minNumPoints = 15;
maxNumPoints = 20;

Estimate the clustering threshold epsilon and display its value on a plot.

clusterDBSCAN.estimateEpsilon(X,minNumPoints,maxNumPoints)

Figure Estimated Epsilon contains an axes object. The axes object with title Estimated Epsilon, xlabel Index, ylabel Epsilon contains 20 objects of type line, text. These objects represent Estimated Epsilon, Time-Averaged Epsilon.

Use the estimated Epsilon value, 3.62, in the clusterDBSCAN clusterer. Then, plot the clusters.

clusterer = clusterDBSCAN('MinNumPoints',6,'Epsilon',3.62, ...
    'EnableDisambiguation',false);
[idx,cidx] = clusterer(X);
plot(clusterer,X,idx)

Figure Clusters contains an axes object. The axes object with title Clusters, xlabel Dimension 1, ylabel Dimension 2 contains 5 objects of type line, scatter, text. One or more of the lines displays its values using only markers

Input Arguments

collapse all

Input feature data, specified as a real-valued N-by-P matrix. The N rows correspond to feature points in a P-dimensional feature space. The P columns contain the values of the features over which clustering takes place. The DBSCAN algorithm can cluster any type of data with appropriate MinNumPoints and Epsilon settings. For example, a two-column input can contain the xy Cartesian coordinates, or range and Doppler.

Data Types: double

The starting value of the k-NN search range, specified as a positive integer. MinNumPoints is used to specify the starting value of k in the k-NN search range. The starting value of k is one less than MinNumPoints.

Example: 10

Data Types: double

The end value of k-NN search range, specified as a positive integer. MaxNumPoints is used to specify the ending value of k in the k-NN search range. The ending value of k is one less than MaxNumPoints.

Output Arguments

collapse all

Estimated epsilon, returned as a positive scalar.

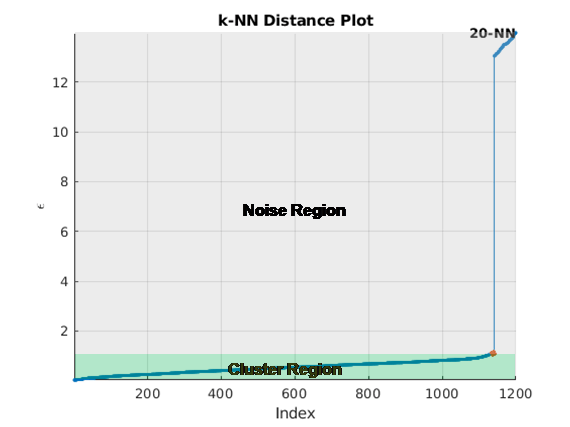
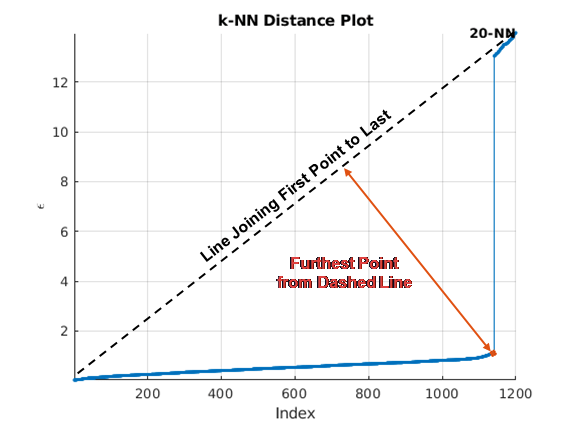
Algorithms

collapse all

Estimate Epsilon

DBSCAN clustering requires a value for the neighborhood size parameter ε. The clusterDBSCAN object and the clusterDBSCAN.estimateEpsilon function use a k-nearest-neighbor search to estimate a scalar epsilon. Let D be the distance of any point P to its kth nearest neighbor. Define a Dk(P)-neighborhood as a neighborhood surrounding P that contains its k-nearest neighbors. There are k + 1 points in the Dk(P)-neighborhood including the point P itself. An outline of the estimation algorithm is:

  • For each point, find all the points in its Dk(P)-neighborhood

  • Accumulate the distances in all Dk(P)-neighborhoods for all points into a single vector.

  • Sort the vector by increasing distance.

  • Plot the sorted k-dist graph, which is the sorted distance against point number.

  • Find the knee of the curve. The value of the distance at that point is an estimate of epsilon.

The figure here shows distance plotted against point index for k = 20. The knee occurs at approximately 1.5. Any points below this threshold belong to a cluster. Any points above this value are noise.

There are several methods to find the knee of the curve. clusterDBSCAN and clusterDBSCAN.estimateEpsilon first define the line connecting the first and last points of the curve. The ordinate of the point on the sorted k-dist graph furthest from the line and perpendicular to the line defines epsilon.

When you specify a range of k values, the algorithm averages the estimate epsilon values for all curves. This figure shows that epsilon is fairly insensitive to k for k ranging from 14 through 19.

To create a single k-NN distance graph, set the MinNumPoints property equal to the MaxNumPoints property.

Choosing the Minimum and Maximum Number of Points

The purpose of MinNumPoints is to smooth the density estimates. Because a cluster is a maximal set of density-connected points, choose smaller values when the expected number of detections in a cluster is unknown. However, smaller values make the DBSCAN algorithm more susceptible to noise. A general guideline for choosing MinNumPoints is:

  • Generally, set MinNumPoints = 2P where P is the number of feature dimensions in X.

  • For data sets that have one or more of the following properties:

    • many noise points

    • large number of points, N

    • large dimensionality, P

    • many duplicates

    increasing MinNumPoints can often improve clustering results.

Extended Capabilities

Version History

Introduced in R2021a

See Also

| |