Main Content

Model Platform Motion Using Trajectory Objects

This topic introduces how to use three different trajectory objects to model platform trajectories, and how to choose between them.

Introduction

Radar Toolbox™ provides three System objects that you can use to model trajectories of platforms including ground vehicles, ships, aircraft, and spacecraft. You can choose between these trajectory objects based on the available trajectory information and the distance span of the trajectory.

  • waypointTrajectory (Sensor Fusion and Tracking Toolbox) — Defines a trajectory using a few waypoints in Cartesian coordinates that the trajectory must pass through. The trajectory assumes the reference frame is a fixed North-East-Down (NED) or East-North-Up (ENU) frame. Since the trajectory interpolation assumes that the gravitational acceleration expressed in the trajectory reference frame is constant, waypointTrajectory is typically used for a trajectory defined within an area that spans only tens or hundreds of kilometers.

  • geoTrajectory (Sensor Fusion and Tracking Toolbox) — Defines a trajectory using a few waypoints in geodetic coordinates (latitude, longitude, and altitude) that the trajectory must pass through. Since the waypoints are expressed in geodetic coordinates, geoTrajectory is typically used for a trajectory from hundreds to thousands of kilometers of distance span.

  • kinematicTrajectory (Sensor Fusion and Tracking Toolbox) — Defines a trajectory using kinematic properties, such as acceleration and angular acceleration, expressed in the platform body frame. You can use kinematicTrajectory to generate a trajectory of any distance span as long as the kinematic information of the trajectory is available. The object assumes a Cartesian coordinate reference frame.

The two waypoint-based trajectory objects (waypointTrajectory and geoTrajectory) can automatically calculate the linear velocity information of the platform, but you can also explicitly specify the linear velocity using the Velocity property or a combination of the Course, GroundSpeed, and ClimbRate properties.

The trajectory of a platform is composed of rotational motion and translational motion. By default, the two waypoint-based trajectory objects (waypointTrajectory and geoTrajectory) automatically generate the orientation of the platform at each waypoint by aligning the yaw angle with the path of the trajectory, but you can explicitly specify the orientation using the Orientation property. Alternately, you can use the AutoPitch and AutoBank properties to enable automatic pitch and roll angles, respectively. For kinematicTrajectory, you need to use the Orientation property and the angular velocity input to specify the rotational motion of the trajectory.

waypointTrajectory

The waypointTrajectory System object defines a trajectory that smoothly passes through waypoints expressed in Cartesian coordinates. Generally, you can use waypointTrajectory to model vehicles travelling within hundreds of kilometers. These vehicles include automobiles, surface marine craft, and commercial aircraft (helicopters, planes, and quadcopters). You can choose the reference frame as a fixed ENU or NED frame using the ReferenceFrame property. For more details on how the object generates the trajectory, see the Algorithms (Sensor Fusion and Tracking Toolbox) section of waypointTrajectory.

waypointTrajectory Example for Aircraft Landing

Open Live Script

Define the trajectory of a landing aircraft using a waypointTrajectory object.

waypoints = [-421 -384 2000;
    47 -294 1600;
    1368 174 1300;
    995 1037 900;
    -285 293 600;
    -1274 84 350;
    -2328 101 150;
    -3209 83 0];
timeOfArrival =  [0; 16.71; 76.00; 121.8; 204.3; 280.31; 404.33; 624.6];
aircraftTraj = waypointTrajectory(waypoints,timeOfArrival);

Create a theaterPlot object to visualize the trajectory and the aircraft.

minCoords = min(waypoints);
maxCoords = max(waypoints);
tp = theaterPlot('XLimits',1.2*[minCoords(1) maxCoords(1)], ...
    'YLimits',1.2*[minCoords(2) maxCoords(2)], ...
    'ZLimits',1.2*[minCoords(3) maxCoords(3)]);

% Create a trajectory plotter and a platform plotter
tPlotter = trajectoryPlotter(tp,'DisplayName','Trajectory');
pPlotter = platformPlotter(tp,'DisplayName','Aircraft');

Obtain the Cartesian waypoints of the trajectory using the lookupPose object function.

sampleTimes = timeOfArrival(1):timeOfArrival(end);
numSteps = length(sampleTimes);
[positions,orientations] = lookupPose(aircraftTraj,sampleTimes);
plotTrajectory(tPlotter,{positions})
axis equal

Plot the platform motion using an airplane mesh object.

mesh = scale(rotate(tracking.scenario.airplaneMesh,[0 0 180]),15); % Exaggerated scale for better visualization
view(20.545,-20.6978)
for i = 1:numSteps
    plotPlatform(pPlotter,positions(i,:),mesh,orientations(i))
    % Uncomment the next line to slow the aircraft motion animation
    % pause(1e-7)
end

In the animation, the yaw angle of the aircraft aligns with the trajectory by default.

Create a second aircraft trajectory with the same waypoints as the first aircraft trajectory, but set its AutoPitch and AutoBank properties to true. This generates a trajectory more representative of the possible aircraft maneuvers.

aircraftTraj2 = waypointTrajectory(waypoints,timeOfArrival, ...
    'AutoPitch',true, ...
    'AutoBank',true);

Plot the second trajectory and observe the change in aircraft orientation.

[positions2,orientations2] = lookupPose(aircraftTraj2,sampleTimes);
for i = 1:numSteps
    plotPlatform(pPlotter,positions2(i,:),mesh,orientations2(i));
    % Uncomment the next line to slow the aircraft motion animation
    % pause(1e-7)
end

Figure contains an axes object. The axes object with xlabel X (m), ylabel Y (m) contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Trajectory, Aircraft.

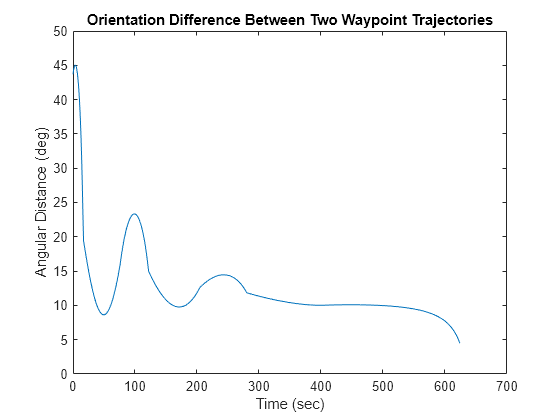
Visualize the orientation differences between the two trajectories in angles.

distance = dist(orientations2,orientations);
figure
plot(sampleTimes,distance*180/pi)
xlabel('Time (sec)')
ylabel('Angular Distance (deg)')
title('Orientation Difference Between Two Waypoint Trajectories')

Figure contains an axes object. The axes object with title Orientation Difference Between Two Waypoint Trajectories, xlabel Time (sec), ylabel Angular Distance (deg) contains an object of type line.

geoTrajectory

The geoTrajectory System object generates a trajectory using waypoints in a similar fashion as the waypointTrajectory object, but it has two major differences in how to specify waypoints and velocity inputs.

  • When specifying waypoints for geoTrajectory, express each waypoint in the geodetic coordinates of latitude, longitude, and altitude above the WG84 ellipsoid model. Using geodetic coordinates, you can conveniently specify long-range trajectories, such as airplane flight trajectory on a realistic Earth model.

  • When specifying the orientation and velocity information for each waypoint, the reference frame for orientation and velocity is the local NED or ENU frame defined under the current trajectory waypoint. For example, the N1-E1-D1 frame shown in the figure is a local NED reference frame.

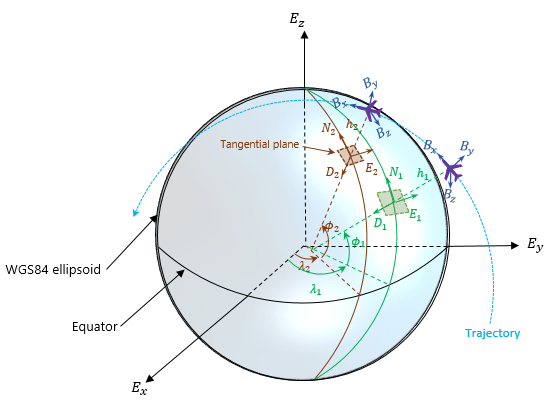
geoTrajectory Reference Frames

In the figure,

  • Ex, Ey, and Ez are the three axes of the Earth-centered Earth-fixed (ECEF) frame, which is fixed on the Earth.

  • (λ1, ϕ1, h1) and (λ2, ϕ2, h2) are the geodetic coordinates of the plane at the two waypoints.

  • (N1, E1, D1) and (N2, E2, D2) are the two local NED frames corresponding to the two trajectory waypoints.

  • Bx, By, and Bz are the three axes of the platform body frame, which is fixed on the platform.

geoTrajectory Example For Flight Trajectory

Open Live Script

Load the flight data of a flight trajectory from Los Angeles to Boston. The data contains flight information including flight time, geodetic coordinates for each waypoint, course, and ground speed.

load flightData.mat

Create a geoTrajectory object based on the flight data.

planeTraj = geoTrajectory([latitudes longitudes heights],timeOfArrival, ...
    'Course',courses,'GroundSpeed',speeds);

Look up the Cartesian coordinates of the waypoints in the ECEF frame.

sampleTimes = 0:1000:3600*10;
positionsCart = lookupPose(planeTraj,sampleTimes,'ECEF');

Show the trajectory using the helperGlobeView class, which approximates the Earth sphere.

viewer = helperGlobeView;
plot3(positionsCart(:,1),positionsCart(:,2),positionsCart(:,3),'r')

You can further explore the trajectory by querying other outputs of the trajectory.

kinematicTrajectory

Unlike the two waypoint trajectory objects, the kinematicTrajectory System object uses kinematic attributes to specify a trajectory. Think of the trajectory as a numerical integration of the pose (position and orientation) and linear velocity of the platform, based on the linear acceleration and angular acceleration information. The pose and linear velocity are specified with respected to a chosen, fixed scenario frame, whereas the linear acceleration and angular velocity are specified with respected to the platform body frame.

kinematicTrajectory Example For UAV Path

Open Live Script

Create a kinematicTrajectory object for simulating a UAV path. Specify the time span of the trajectory as 120 seconds.

traj = kinematicTrajectory('SampleRate',1, ...
    'AngularVelocitySource','Property');

tStart = 0;
tFinal = 120;
tspan = tStart:tFinal;

numSteps = length(tspan);
positions = NaN(3,numSteps);
velocities = NaN(3,numSteps);
vel = NaN(1,numSteps);

To form a square path covering a small region, separate the UAV trajectory into six segments:

  • Taking off and ascending in the z-direction

  • Moving in the positive x-direction

  • Moving in the positive y-direction

  • Moving in the negative x-direction

  • Moving in the negative y-direction

  • Descending in the z-direction and landing

In each segment, the UAV accelerates in one direction and then decelerates in that direction with the same acceleration magnitude. As a result, at the end of each segment, the velocity of the UAV is zero.

segSteps = floor(numSteps/12);
accelerations = zeros(3,numSteps);
acc = 1;
% Acceleration for taking off and ascending in the z-direction
accelerations(3,1:segSteps) = acc;
accelerations(3,segSteps+1:2*segSteps) = -acc;

% Acceleration for moving in the positive x-direction
accelerations(1,2*segSteps+1:3*segSteps) = acc;
accelerations(1,3*segSteps+1:4*segSteps) = -acc;

% Acceleration for moving in the positive y-direction
accelerations(2,4*segSteps+1:5*segSteps) = acc;
accelerations(2,5*segSteps+1:6*segSteps) = -acc;

% Acceleration for moving in the negative x-direction
accelerations(1,6*segSteps+1:7*segSteps) = -acc;
accelerations(1,7*segSteps+1:8*segSteps) = acc;

% Acceleration for moving in the negative y-direction 
accelerations(2,8*segSteps+1:9*segSteps) = -acc;
accelerations(2,9*segSteps+1:10*segSteps) = acc;

% Descending in the z-direction and landing
accelerations(3,10*segSteps+1:11*segSteps) =-acc;
accelerations(3,11*segSteps+1:end) = acc;

Simulate the trajectory by calling the kinematicTrajectory object with the specified acceleration.

for i = 1:numSteps
    [positions(:,i),~,velocities(:,i)] = traj(accelerations(:,i)');  
     vel(i) = norm(velocities(:,i));
end

Visualize the trajectory using theaterPlot.

% Create a theaterPlot object and create plotters for the trajectory and the
% UAV Platform.
figure
tp = theaterPlot('XLimits',[-30 130],'YLimits',[-30 130],'ZLimits',[-30 130]);
tPlotter = trajectoryPlotter(tp,'DisplayName','UAV trajectory');
pPlotter = platformPlotter(tp,'DisplayName','UAV','MarkerFaceColor','g');

% Plot the trajectory.
plotTrajectory(tPlotter,{positions'})
view(-43.18,56.49)

% Use a cube to represent the UAV platform.
dims = struct('Length',10, ...
    'Width',5, ...
    'Height',3, ...
    'OriginOffset',[0 0 0]);

% Animate the UAV platform position.
for i = 1:numSteps
    plotPlatform(pPlotter,positions(:,i)',dims,eye(3))
    pause(0.01)
end

Figure contains an axes object. The axes object with xlabel X (m), ylabel Y (m) contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent UAV trajectory, UAV.

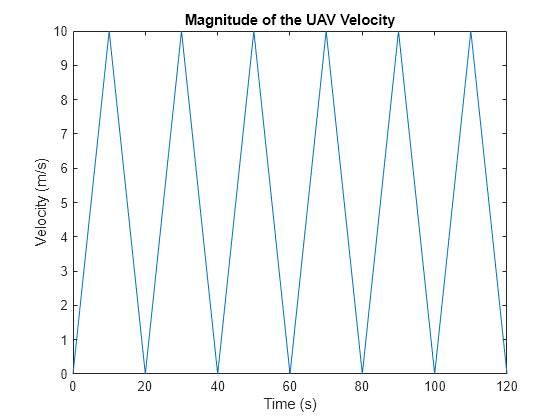
Show the velocity magnitude of the UAV platform.

figure
plot(tspan,vel)
xlabel('Time (s)')
ylabel('Velocity (m/s)')
title('Magnitude of the UAV Velocity')

Figure contains an axes object. The axes object with title Magnitude of the UAV Velocity, xlabel Time (s), ylabel Velocity (m/s) contains an object of type line.

kinematicTrajectory Example For Spacecraft Trajectory

Open Live Script

Use kinematicTrajetory to specify a circular spacecraft trajectory. The orbit has these elements:

  • Orbital radius (r) — 7000 km

  • Inclination (i) — 60 degrees

  • Argument of ascending node (Ω) — 90 degrees. The ascending node direction is aligned with the Y-direction.

  • True anomaly (ν) — –90 degrees

In the figure, X-Y-Z is the Earth-centered inertial (ECI) frame, which has a fixed position and orientation in space. x-y-z is the spacecraft body frame, fixed on the spacecraft. r→ and v→ are the initial position and velocity of the spacecraft.

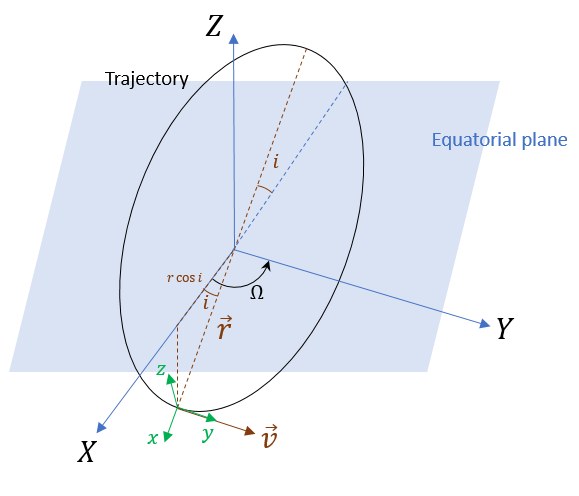
To specify the circular orbit using kinematicTrajectory, you need to provide the initial position, initial velocity, and initial orientation of the spacecraft with respect to the ECI frame. For the chosen true anomaly (v = –90∘), the spacecraft velocity is aligned with the Y-direction.

inclination = 60; % degrees
mu = 3.986e14; % standard earth gravitational parameter
radius = 7000e3;% meters
v = sqrt(mu/radius); % speed
initialPosition = [radius*cosd(inclination),0,-radius*sind(inclination)]';
initialVelocity = [0 v 0]';

Assume the x-direction of the spacecraft body frame is the radial direction, the z-direction is the normal direction of the orbital plane, and the y-direction completes the right-hand rule. Use the assumptions to specify the orientation of the body frame at the initial position.

orientation = quaternion([0 inclination 0],'eulerd','zyx','frame');

Express the angular velocity and the angular acceleration of the trajectory in the platform body frame.

omega = v/radius;
angularVelocity = [0 0 omega]';
a = v^2/radius;
acceleration = [-a 0 0]';

Set a simulation time of one orbital period. Specify a simulation step as 2 seconds.

tFinal = 2*pi/omega;
dt = 2;
sampleRate = 1/dt;
tspan = 0:dt:tFinal;
numSteps = length(tspan);

Create the spacecraft trajectory. Since the acceleration and angular velocity of the spacecraft remain constant with respect to the spacecraft body frame, specify them as constants. Generate position and orientation outputs along the trajectory by using the kinematicTrajectory object. 

traj = kinematicTrajectory('SampleRate',sampleRate, ...
    'Position',initialPosition, ...
    'Velocity',initialVelocity, ...
    'Orientation',orientation, ...
    'AngularVelocity',angularVelocity, ...
    'Acceleration',acceleration, ...
    'AccelerationSource','Property', ...
    'AngularVelocitySource','Property');

% Generate position and orientation outputs.
positions = NaN(3,numSteps);
orientations = zeros(numSteps,1,'quaternion');
for i = 1:numSteps    
   [positions(:,i),orientations(i)] = traj();     
end

Use the helperGlobeView class and theaterPlot to show the trajectory.

viewer = helperGlobeView(0,[60 0]);
tp = theaterPlot('Parent',gca,...
    'XLimits',1.2*[-radius radius],...
    'YLimits',1.2*[-radius radius],...
    'ZLimits',1.2*[-radius radius]);
tPlotter = trajectoryPlotter(tp,'LineWidth',2);
pPlotter = platformPlotter(tp,'MarkerFaceColor','m');
legend(gca,'off')

plotTrajectory(tPlotter,{positions'})
% Use a cube with exaggerated dimensions to represent the spacecraft.
dims = struct('Length',8e5,'Width',4e5,'Height',2e5,'OriginOffset',[0 0 0]);

for i = 1:numSteps    
   plotPlatform(pPlotter,positions(:,i)',dims,orientations(i))
   % Since the reference frame is the ECI frame, earth rotates with respect to it.
   rotate(viewer,dt)
end

Figure contains an axes object. The hidden axes object with xlabel X (m), ylabel Y (m) contains an object of type surface.

Summary

In this topic, you learned how to use three trajectory objects to customize your own trajectories based on the available information. In addition, you learned the fundamental differences in applying them. This table highlights the main attributes of these trajectory objects.

Trajectory ObjectPosition InputsLinear Velocity Inputs OrientationAcceleration and Angular Velocity InputsRecommended Distance Span
waypointTrajectoryCartesian waypoints expressed in a fixed frame (NED or ENU)

One of these options:

  • Automatically generate velocity for a smooth trajectory, by default

  • Specify velocity in the fixed frame at each waypoint

  • Specify course, ground speed, and climb rate in the fixed frame at each waypoint

One of these options:

  • Auto yaw by default, auto pitch by selection, and auto bank by selection

  • Specify orientation in the fixed frame

Cannot specify From within tens to hundreds of kilometers
geoTrajectory Geodetic waypoints in the ECEF frame

One of these options:

  • Automatically generate velocity for a smooth trajectory, by default

  • Specify velocity in the local frame (NED or ENU) for each waypoint

  • Specify course, ground speed, and climb rate in the local frame (NED or ENU) for each waypoint

One of these options:

  • Auto yaw by default, auto pitch by selection, and auto bank by selection

  • Specify orientation in the local frame

Cannot specifyFrom hundreds to thousands of kilometers
kinematicTrajectoryInitial position expressed in a chosen, fixed frame Only initial velocity in the fixed frameOnly initial orientation in the fixed frame Specify acceleration and angular velocity in the platform body frame Unlimited distance span