kinematicTrajectory
Rate-driven trajectory generator
Description
The kinematicTrajectory
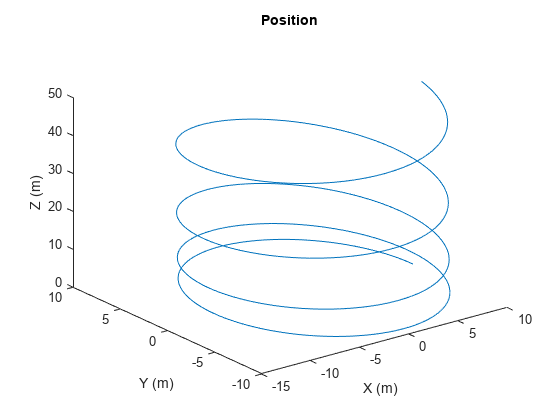
System object™ generates trajectories using specified acceleration and angular velocity.
To generate a trajectory from rates:
Create the
kinematicTrajectoryobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
trajectory = kinematicTrajectorytrajectory, that generates a trajectory based on
acceleration and angular velocity.
trajectory = kinematicTrajectory(Name,Value)Name to the specified Value.
Unspecified properties have default values.
Example: trajectory =
kinematicTrajectory('SampleRate',200,'Position',[0,1,10]) creates a kinematic
trajectory System object, trajectory, with a sample rate of 200 Hz and
the initial position set to [0,1,10].
Properties
Usage
Syntax
Description
[
outputs the trajectory state and then updates the trajectory state based on
position,orientation,velocity,acceleration,angularVelocity] = trajectory(bodyAcceleration,bodyAngularVelocity)bodyAcceleration and bodyAngularVelocity.
This syntax is only valid if AngularVelocitySource is set to
'Input' and AccelerationSource is set to
'Input'.
[
outputs the trajectory state and then updates the trajectory state based on
position,orientation,velocity,acceleration,angularVelocity] = trajectory(bodyAngularVelocity)bodyAngularVelocity.
This syntax is only valid if AngularVelocitySource is set to
'Input' and AccelerationSource is set to
'Property'.
[
outputs the trajectory state and then updates the trajectory state based on
position,orientation,velocity,acceleration,angularVelocity] = trajectory(bodyAcceleration)bodyAcceleration.
This syntax is only valid if AngularVelocitySource is set to
'Property' and AccelerationSource is set to
'Input'.
[
outputs the trajectory state and then updates the trajectory state.position,orientation,velocity,acceleration,angularVelocity] = trajectory()
This syntax is only valid if AngularVelocitySource is set to
'Property' and AccelerationSource is set to
'Property'.
Input Arguments
Output Arguments
Object Functions
Examples
Extended Capabilities
Version History
Introduced in R2018b