Main Content

platform

Add platform to tracking scenario

expand all in page

Syntax

ptfm = platform(sc)
ptfm = platform(sc,Name,Value)

Description

ptfm = platform(sc) adds a Platform object, ptfm, to the tracking scenario, sc. The function creates a platform with default property values. Platforms are defined as points or cuboids with aspect-dependent properties. Each platform is automatically assigned a unique ID specified in the platformID field of the Platform object.

ptfm = platform(sc,Name,Value) adds a platform with additional properties specified by one or more Name,Value pair arguments. Name is a property name and Value is the corresponding value. Name must appear inside single quotes (''). You can specify several name-value pair arguments in any order as Name1,Value1,...,NameN,ValueN. Any unspecified properties take default values.

Input Arguments

expand all

Tracking scenario, specified as a trackingScenario object.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Platform classification identifier specified as a nonnegative integer. You can define your own platform classification scheme and assign ClassID values to platforms according to the scheme. The value of 0 is reserved for an object of unknown or unassigned class.

Example: 5

Data Types: double

This property is read-only.

Current position of the platform, specified as a 3-element vector of scalars.

  • When the IsEarthCentered property of the scenario is set to false, the position is specified as a three element Cartesian state [x, y, z] in meters.

  • When the IsEarthCentered property of the scenario is set to true, the position is specified as a three element geodetic state: latitude in degrees, longitude in degrees, and altitude in meters.

You should only specify position when creating a stationary platform. If you choose to specify the trajectory of the platform, do not use Position. Instead, use the Trajectory argument.

Data Types: double

This property is read-only.

Orientation of the platform, specified as a 3-element vector of scalars in degrees. The three scalars are the [yaw, pitch, roll] rotation angles from the local reference frame to the platform's body frame.

You should only specify Orientation when creating a stationary platform. If you choose to specify the orientation over time, use the Trajectory argument.

Data Types: double

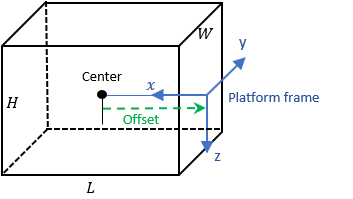
Platform dimensions and origin offset, specified as a structure. The structure contains the Length, Width, Height, and OriginOffset of a cuboid that approximates the dimensions of the platform. The OriginOffset is the position vector from the center of the cuboid to the origin of the platform coordinate frame. The OriginOffset is expressed in the platform coordinate system. For example, if the platform origin is at the center of the cuboid rear face as shown in the following figure, then set OriginOffset as [-L/2, 0, 0]. The default value for Dimensions is a structure with all fields set to zero, which corresponds to a point model.

Dimensions of Platform

Fields of Dimensions

FieldsDescriptionDefault
LengthDimension of a cuboid along the x direction0
WidthDimension of a cuboid along the y direction0
HeightDimension of a cuboid along the z direction0
OriginOffsetPosition of the platform coordinate frame origin with respect to the cuboid center[0 0 0 ]

Example: struct('Length',5,'Width',2.5,'Height',3.5,'OriginOffset',[-2.5 0 0])

Data Types: struct

Platform motion, specified as either a kinematicTrajectory object, a waypointTrajectory object, or a geoTrajectory object. The trajectory object defines the time evolution of the position and velocity of the platform frame origin, as well as the orientation of the platform frame relative to the scenario frame.

Platform signatures, specified as a cell array of irSignature, rcsSignature, and tsSignature objects or an empty cell array. The cell array contains at most only one instance for each type of signature objects listed. A signature represents the reflection or emission pattern of a platform such as its radar cross-section, target strength, or IR intensity.

A pose estimator, specified as a pose estimator object. The pose estimator determines platform pose with respect to the local NED scenario coordinate. The interface of any pose estimator must match the interface of insSensor. By default, pose estimator accuracy properties are set to zero.

Emitters mounted on the platform, specified as a cell array of emitter objects, such as radarEmitter or sonarEmitter.

Sensors mounted on platform, specified as a cell array of sensor objects such as irSensor, fusionRadarSensor, monostaticLidarSensor, or sonarSensor.

Output Arguments

expand all

Scenario platform, returned as a Platform object.

Examples

expand all

Open Live Script

Create a tracking scenario and a platform following a circular path.

scene = trackingScenario('UpdateRate',1/50);

% Create a platform
plat = platform(scene);

% Follow a circular trajectory 1 km in radius completing in 400 hundred seconds.
plat.Trajectory = waypointTrajectory('Waypoints', [0 1000 0; 1000 0 0; 0 -1000 0; -1000 0 0; 0 1000 0], ...
    'TimeOfArrival', [0; 100; 200; 300; 400]);

% Perform the simulation
while scene.advance
    p = pose(plat);
    fprintf('Time = %f ', scene.SimulationTime);
    fprintf('Position = [');
    fprintf('%f ', p.Position);
    fprintf('] Velocity = [');
    fprintf('%f ', p.Velocity);
    fprintf(']\n');
end
Time = 0.000000 

Position = [

0.000000 1000.000000 0.000000 

] Velocity = [

15.707701 -0.000493 0.000000 

]

Time = 50.000000 

Position = [

707.095476 707.100019 0.000000 

] Velocity = [

11.107152 -11.107075 0.000000 

]

Time = 100.000000 

Position = [

1000.000000 0.000000 0.000000 

] Velocity = [

0.000476 -15.707961 0.000000 

]

Time = 150.000000 

Position = [

707.115558 -707.115461 0.000000 

] Velocity = [

-11.107346 -11.107341 0.000000 

]

Time = 200.000000 

Position = [

0.000000 -1000.000000 0.000000 

] Velocity = [

-15.707963 0.000460 0.000000 

]

Time = 250.000000 

Position = [

-707.098004 -707.098102 0.000000 

] Velocity = [

-11.107069 11.107074 0.000000 

]

Time = 300.000000 

Position = [

-1000.000000 0.000000 0.000000 

] Velocity = [

-0.000476 15.707966 0.000000 

]

Time = 350.000000 

Position = [

-707.118086 707.113543 0.000000 

] Velocity = [

11.107262 11.107340 0.000000 

]

Time = 400.000000 

Position = [

-0.000000 1000.000000 0.000000 

] Velocity = [

15.708226 -0.000493 0.000000 

]
Open Live Script

Create a tracking scenario with two cuboid platforms following circular trajectories.

sc = trackingScenario;

% Create the platform for a truck with dimension 5 x 2.5 x 3.5 (m). 
p1 = platform(sc);
p1.Dimensions = struct('Length',5,'Width',2.5,'Height',3.5,'OriginOffset',[0 0 0]);

% Specify the truck's trajectory as a circle with radius 20 meters.
p1.Trajectory = waypointTrajectory('Waypoints', [20*cos(2*pi*(0:10)'/10)...
                              20*sin(2*pi*(0:10)'/10) -1.75*ones(11,1)], ...
                              'TimeOfArrival', linspace(0,50,11)');
                    
% Create the platform for a small quadcopter with dimension .3 x .3 x .1 (m).
p2 = platform(sc);
p2.Dimensions = struct('Length',.3,'Width',.3,'Height',.1,'OriginOffset',[0 0 0]);

% The quadcopter follows the truck at 10 meteres above with small angular delay.
% Note that the negative z coordinates correspond to positive elevation.
p2.Trajectory = waypointTrajectory('Waypoints', [20*cos(2*pi*((0:10)'-.6)/10)...
                               20*sin(2*pi*((0:10)'-.6)/10) -11.80*ones(11,1)], ...
                               'TimeOfArrival', linspace(0,50,11)');

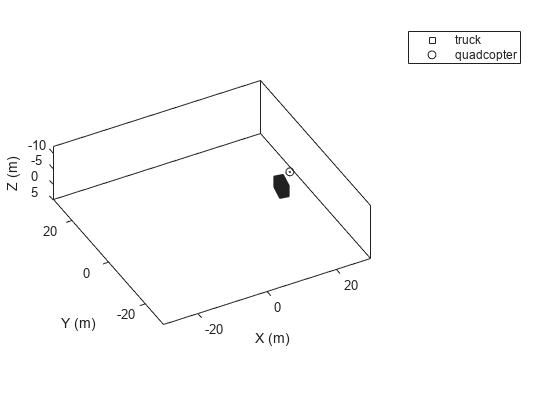
Visualize the results using theaterPlot.

tp = theaterPlot('XLim',[-30 30],'YLim',[-30 30],'Zlim',[-12 5]);
pp1 = platformPlotter(tp,'DisplayName','truck','Marker','s');
pp2 = platformPlotter(tp,'DisplayName','quadcopter','Marker','o');

% Specify a view direction and animate.
view(-28,37);
set(gca,'Zdir','reverse');

while advance(sc)
    poses = platformPoses(sc);
    plotPlatform(pp1, poses(1).Position, p1.Dimensions, poses(1).Orientation);
    plotPlatform(pp2, poses(2).Position, p2.Dimensions, poses(2).Orientation);
end

Figure contains an axes object. The axes object with xlabel X (m), ylabel Y (m) contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent truck, quadcopter.

Version History

Introduced in R2018b

See Also

Objects