Main Content

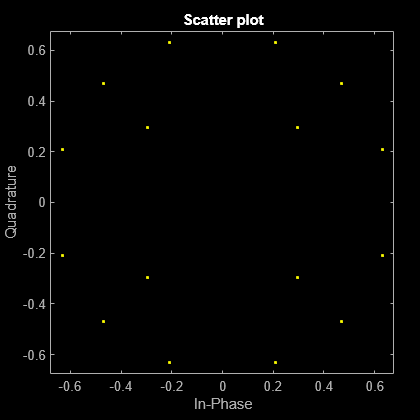
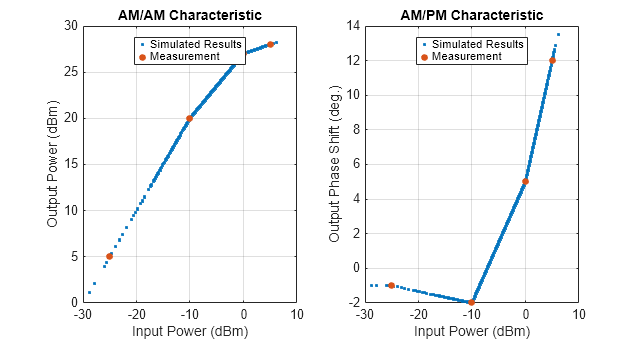
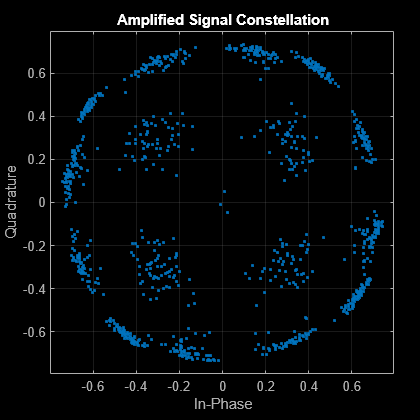
rf.Amplifier

Model nonlinear amplifiers using cubic polynomial, AM/AM-AM/PM, modified Rapp, or Saleh representations

Since R2024b

expand all in page

Description

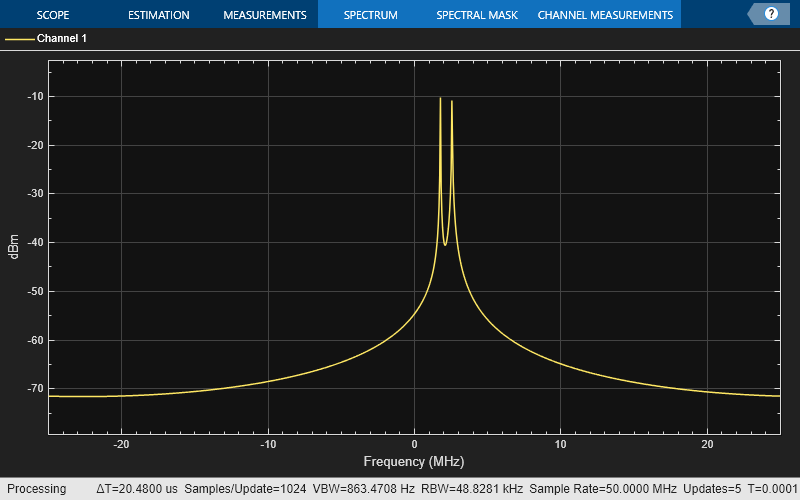
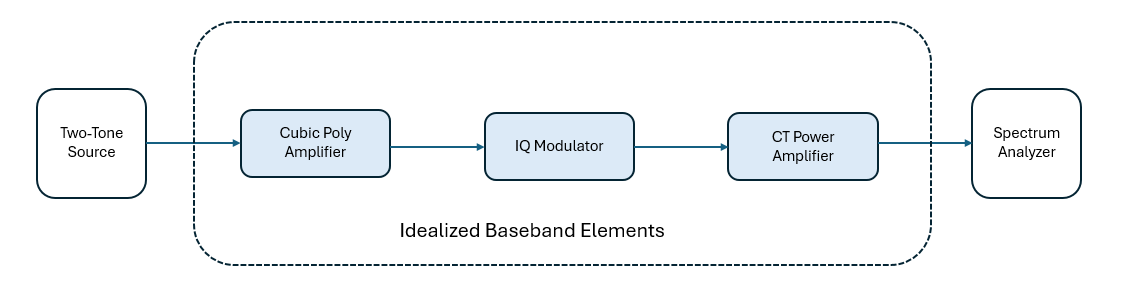
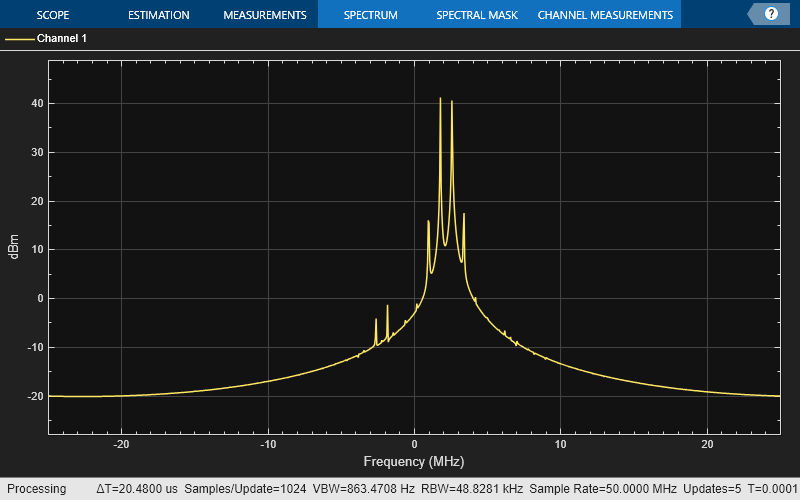
Use the rf.Amplifier System object™ to create an idealized amplifier for command line simulation. The rf.Amplifier System object is a complex baseband model of an idealized amplifier with thermal noise. This System object provides four nonlinearity models and three options to specify noise representation. The four nonlinearity models are cubic polynomial, AM/AM-AM/PM, modified Rapp, and Saleh.

To create a complex baseband model of amplifier with noise and nonlinearities:

  1. Create the rf.Amplifier object and set its properties.

  2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

rfamp = rf.Amplifier
rfamp = rf.Amplifier(Name=Value)

Description

rfamp = rf.Amplifier creates an idealized amplifier that allows you to process complex baseband signals with noise and nonlinearities.

example

rfamp = rf.Amplifier(Name=Value) sets properties of the rf.Amplifier object using one or more name-value arguments. For example, rfamp = rf.Amplifier(Model='ampm') creates an idealized amplifier element designed using AM/AM—AM/PM data. Properties you do not specify retain their default values.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Model

Specify the amplifier nonlinearity model as one of the following:

  • cubic — The cubic polynomial model uses linear power gain to determine the linear coefficient of a third-order polynomial and either IP3, P1dB, or Psat to determine the third - order coefficient of the polynomial.

  • ampm — The AM/AM-AM/PM model uses a lookup table to calculate the amplifier power characteristics.

  • modified-rapp — The modified Rapp model uses a normalized transfer function to calculate the amplifier power characteristics.

  • saleh — The Saleh model also uses a normalized transfer function to calculate the amplifier power characteristics.

For more information, see Nonlinearity Models in Idealized Amplifier Block (RF Blockset).

Cubic Polynomial

Linear power gain for a cubic amplifier model, specified as a real number in dB. To enable this property, set Model to cubic.

Dependencies

To enable this property, set Model to cubic.

Third order nonlinearity type for the cubic amplifier model, specified as IIP3, OIP3, IP1dB, OP1dB, IPsat, or OPsat.

Dependencies

To enable this property, set Model to cubic.

Input third-order intercept point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Model to cubic and Nonlinearity to IIP3.

Output third-order intercept point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Model to cubic and Nonlinearity to OIP3.

Input 1 dB compression point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Model to cubic and Nonlinearity to IP1dB.

Output 1 dB compression point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Model to cubic and Nonlinearity to OP1dB.

Input saturation point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Model to cubic and Nonlinearity to IPsat.

Output saturation point, specified as a positive real number in dBm.

Dependencies

To enable this property, set Model to cubic and Nonlinearity to OPsat.

AM/AM - AM/PM

AM/AM - AM/PM lookup table entries, specified as a real M-by-3 matrix. This matrix expresses the output power in dBm in the second column and the phase change in degrees in the third column. The values in the second and third columns are relative to the absolute value of the input signal power in dBm in the first column. The values in the first column must increase monotonically.

Dependencies

To enable this property, set Model to ampm.

Modified Rapp

Magnitude gain for the modified Rapp amplifier model AM/AM calculations, specified as a real positive number in dB.

Dependencies

To enable this property, set Model to modified-rapp.

Voltage output saturation level for the modified Rapp amplifier model, specified as a real positive number in dBm.

Dependencies

To enable this property, set Model to modified-rapp.

Magnitude smoothness factor for the modified Rapp amplifier model in AM/AM calculations, specified as a positive real number.

Dependencies

To enable this property, set Model to modified-rapp.

Phase gain for the modified Rapp amplifier model in AM/PM calculations, specified as a real scalar in radians.

Dependencies

To enable this property, set Model to modified-rapp.

Phase saturation for the modified Rapp amplifier model in AM/PM calculations, specified as a positive real number.

Dependencies

To enable this property, set Model to modified-rapp.

Phase smoothness factor for the modified Rapp amplifier model in AM/PM calculations, specified as a positive real scalar or two-tuple vector.

Dependencies

To enable this property, set Model to modified-rapp.

Saleh

Input signal level scaling factor for the Saleh amplifier model, specified as a real number in dB.

Dependencies

To enable this property, set Model to saleh.

AM/AM 2-tuple [alpha beta] conversion parameters for the Saleh amplifier model, specified as a two-element row vector of real scalars.

Dependencies

To enable this property, set Model to saleh.

AM/PM 2-tuple [alpha beta] conversion parameters for the Saleh amplifier model, specified as a two-element row vector of real scalars.

Dependencies

To enable this property, set Model to saleh.

Output signal level scaling factor for the Saleh amplifier model, specified as real number in dB.

Dependencies

To enable this property, set Model to saleh.

Noise Properties

Options to add system noise to the input signal, specified as a logical 1 (true) or 0 (false).

Noise representation method, specified as noise-temperature, NF, or noise-factor.

For more information, see Thermal Noise Simulations in Idealized Amplifier Block (RF Blockset).

Dependencies

To enable this property, set IncludeNoise to 1 or true.

Noise temperature to model noise in the amplifier, specified as a nonnegative real number in degrees (K).

Dependencies

To enable this property, set IncludeNoiseto 1 or true and set NoiseType to noise-temperature.

Noise figure to model noise in the amplifier, specified as a nonnegative real number in dB.

Dependencies

To enable this property, set IncludeNoiseto 1 or true and set NoiseType to NF.

Noise factor to model noise in the amplifier, specified as a positive integer scalar greater than or equal to 1.

Dependencies

To enable this property, set IncludeNoiseto 1 or true and set NoiseType to noise-factor.

Source of initial seed used to prepare the Gaussian random number noise generator, specified as one of the following:

  • auto — When you set SeedSource to auto, the object generates seeds for each amplifier instance using a random number generator. The reset method of the instance has no effect.

  • user — When you set SeedSource to user, the object uses value you provide in the Seed property to initialize the random number generator. The reset method resets the random number generator using the Seed property value.

Dependencies

To enable this property, set IncludeNoise to 1 or true.

Seed for the random number generator, specified as a nonnegative integer less than 232. Use this value to initialize the random number generator.

Dependencies

To enable this property, set IncludeNoise to 1 or true and set SeedSource to user.

Sample rate, specified as a nonnegative integer of data type double in samples per second.

Dependencies

To enable this property, set IncludeNoise to 1 or true.

Usage

Syntax

out = rfamp(in)

Description

out = rfamp(in) returns the amplified output baseband signal out based on the input baseband signal in.

example

Input Arguments

expand all

Input baseband signal, specified as a real scalar, real column, complex scalar, or complex column.

Data Types: double | single

Output

expand all

Output baseband signal, returned as a real scalar, real column, complex scalar, or complex column. The output port mimics the properties of the input port. For example, if the input baseband signal is specified as a real scalar of the data type double, then the output baseband signal is also a real signal of the data type double.

Data Types: double | single

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

stepRun System object algorithm
releaseRelease resources and allow changes to System object property values and input characteristics
resetReset internal states of System object

Examples

collapse all

This example uses:

Open Live Script

Create an rf.Amplifier System object.

rfAmp = rf.Amplifier('Nonlinearity','IPsat','IPsat',30);

Generate modulated symbols.

in = qammod(randi([0 15],1000,1),16,'UnitAveragePower',true);

Apply the nonlinearity model to the signal and plot the results.

out = rfAmp(in);
scatterplot(out)

Figure Scatter Plot contains an axes object. The axes object with title Scatter plot, xlabel In-Phase, ylabel Quadrature contains a line object which displays its values using only markers. This object represents Channel 1.

This example uses:

Open Live Script

Define modulation order, samples per symbol, and input power.

M = 16;         
sps = 4;        
pindBm = 0;

Create an rf.Amplifier System object defined using an AM/AM-AM/PM nonlinearity model.

 rfamp = rf.Amplifier('Model','ampm');

Apply pulse shaping by interpolating an input signal using a raised cosine finite impulse response (FIR) filter.

txfilter = comm.RaisedCosineTransmitFilter('RolloffFactor',0.3,...
  'FilterSpanInSymbols',6,'OutputSamplesPerSymbol',sps,'Gain',sqrt(sps));

Define input signal.

pin = 10.^((pindBm-30)/10);     % Unit: W
data = randi([0 M-1],1000,1);

Define the modulated, filtered, and amplified signal.

modSig = qammod(data,M,'UnitAveragePower',true)*sqrt(pin);
filtSig = txfilter(modSig);
ampSig = rfamp(filtSig);

Calculate the amplified output signal.

poutdBm = (20*log10(abs(ampSig)))+30;
simulated_pindBm = (20*log10(abs(filtSig)))+30;
phase = angle(ampSig .* conj(filtSig)) * 180/pi;

Plot the AM/AM-AM/PM characteristic of the amplifier by plotting the input vs. output power in a dBm plot.

  figure
  set(gcf,'units','normalized','position',[.25 1/3 .5 1/3])
  subplot (1,2,1)
  pow_idx = simulated_pindBm>-30;
  plot(simulated_pindBm(pow_idx), poutdBm(pow_idx),'.')
  hold on
  plot(rfamp.Table(:,1),rfamp.Table(:,2),'.','Markersize',15)
  xlabel('Input Power (dBm)')
  ylabel('Output Power (dBm)')
  grid on
  title('AM/AM Characteristic')
  Legend = {'Simulated Results','Measurement'};
  legend (Legend, 'Location' , 'north')

Plot the input power (dBm) vs. output phase shift (deg).

  subplot(1,2,2)  
  plot(simulated_pindBm(pow_idx),phase(pow_idx),'.')
  hold on
  plot(rfamp.Table(:,1),rfamp.Table(:,3),'.','Markersize',15)
  legend(Legend,'Location','north')
  xlabel('Input Power (dBm)')
  ylabel('Output Phase Shift (deg.)')
  grid on
  title('AM/PM Characteristic')

Figure contains 2 axes objects. Axes object 1 with title AM/AM Characteristic, xlabel Input Power (dBm), ylabel Output Power (dBm) contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Simulated Results, Measurement. Axes object 2 with title AM/PM Characteristic, xlabel Input Power (dBm), ylabel Output Phase Shift (deg.) contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Simulated Results, Measurement.

Plot the amplified signal in a constellation plot.

  scatterplot(ampSig,sps,0,'.')
  grid on
  title('Amplified Signal Constellation')

Figure Scatter Plot contains an axes object. The axes object with title Amplified Signal Constellation, xlabel In-Phase, ylabel Quadrature contains a line object which displays its values using only markers. This object represents Channel 1.

This example uses:

Open Live Script

This example shows how to input a two-tone signal to an idealized system. To design this RF system:

  • First, generate a two-tone source.

  • Second, connect this two-tone source to an idealized RF PA.

  • Finally, observe the output response of this system.

Introduction

The RF system designed in this example uses the Idealized Baseband System object™ to analyze a cascade of mathematical models of RF components within the MATLAB® environment. During analysis, these System objects uses complex-baseband representation of the RF elements to compute time-domain waveforms. These complex modulated signals represent the transmitted information, assumed to be centered around an implicit carrier frequency. The models from the Idealized Baseband library do not model out-of-band behavior or spurious harmonics generated by nonlinear effects or interfering signals. Additionally, models from the Idealized Baseband library do not model impedance mismatches and assume that all blocks are perfectly matched. As a result, RF models built with the Idealized Baseband library simulate rapidly.

Create Two-Tone Source Generator

This figure shows the architecture of a two-tone source generator. This generator consists of a sine wave generator that produces two sinusoidal signals. These signals are multiplied by a -40 dB gain and then processed by a summer.

signalgen.png

Define sample rate and samples per frame of the sine wave signals.

sampleRate = 1/2e-8;
samplesPerFrame = 512;

Define a gain of - 40 dB.

m40dB = 10^(-40/20); % Request Jeff: Why -40 dB?

Create two sinusoid signals at 1.8 GHz and 2.6 GHz.

SineObj1 = dsp.SineWave('Frequency',1.8e6,'SampleRate',sampleRate,      ...
    SamplesPerFrame=samplesPerFrame,ComplexOutput=true);
SineObj2 = dsp.SineWave('Frequency',2.6e6,'SampleRate',sampleRate,      ...
    SamplesPerFrame=samplesPerFrame,ComplexOutput=true);

Display the spectral analysis of a two tone signal source, where each tone is -10 dBm.

SpectAnal = spectrumAnalyzer('SampleRate',sampleRate,'ShowLegend',true);

for Iter = 1:10
    sineWave1 = SineObj1();
    sineWave2 = SineObj2();
    sigIn = m40dB*(sineWave1 + sineWave2);
    SpectAnal(sigIn);
end

Simulate Idealized System

This figure shows how to create a system to IQ modulate the two-tone signal and amplify using an RF PA. The system architecture involves connecting a cubic polynomial amplifier to an IQ modulator. The output from the IQ modulator is then connected to a cross-term (CT) memory power amplifier. A two-tone signal is supplied as input to the system, and the output is connected to a spectrum analyzer for visualizing the power amplifier characteristics.

twotonesystem.png

Load the pre-computed PA coefficient matrix.

load('PAcoefficients_rf.mat','fitCoefMat')

Create an idealized baseband cubic polynomial amplifier and IQ modulator with nonlinearity and noise.

preAmpIQ = rf.Amplifier('Gain',8,'Nonlinearity','IIP3','IIP3',45,       ...
    'IncludeNoise',true,NF=1.5);
mixerModIQ = rf.Mixer('Model','iqmod','Gain',0,'LO',1e8,                ...
    'PhaseImbalance',.5,'Nonlinearity','IIP3',IIP3=50,                  ...
    IncludeNoise=true,NoiseType='NF',NF=6);

Create an idealized baseband cross-term memory PA. 

powerAmp = rf.PAmemory('Model','Cross-term memory',                     ...
    'CoefficientMatrix','fitCoefMat');

Connect the RF chain and provide the two-tone signal as input. 

SpectAnal = spectrumAnalyzer('SampleRate',sampleRate,'ShowLegend',true);

for Iter = 1:10
    sineWave1 = SineObj1();
    sineWave2 = SineObj2();
    sineIn = m40dB*(sineWave1 + sineWave2);
    ampIQ = preAmpIQ(sineIn);
    modIQ = mixerModIQ(ampIQ);
    paOut = powerAmp(modIQ*sqrt(50))/sqrt(50);

    SpectAnal(paOut);
end

References

[1] Razavi, Behzad. “Basic Concepts “ in RF Microelectronics, 2nd edition, Prentice Hall, 2012.

[2] Rapp, C., “Effects of HPA-Nonlinearity on a 4-DPSK/OFDM-Signal for a Digital Sound Broadcasting System.” Proceedings of the Second European Conference on Satellite Communications, Liege, Belgium, Oct. 22-24, 1991, pp. 179-184.

[3] Saleh, A.A.M., “Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers.” IEEE Trans. Communications, vol. COM-29, pp.1715-1720, November 1981.

[4] IEEE 802.11-09/0296r16. “TGad Evaluation Methodology.“ Institute of Electrical and Electronics Engineers.https://www.ieee.org/

[5] Kundert, Ken.“ Accurate and Rapid Measurement of IP2 and IP3,“ The Designer Guide Community, May 22, 2002.

Version History

Introduced in R2024b

See Also

Blocks