latency

Calculate propagation delay from one asset to another asset

Since R2023a

Syntax

delay = latency(source,target)

[delay,timeOut] = latency(source,target)

[___] = latency(source,target,timeIn)

Description

delay = latency(source,target) calculates the history of propagation delays from the source asset to the target asset. The source and target assets must belong to the same satelliteScenario object. If the value of the AutoSimulate property of the satelliteScenario object is true, the latency function returns the propagation delay history from the value of StartTime to the value of StopTime. Otherwise, it returns the propagation delay history from StartTime to SimulationTime.

[delay,timeOut] = latency(source,target) returns the history of time samples timeOut.

[___] = latency(source,target,timeIn) calculates latency at the specified datetime timeIn. When using this syntax, the latency function sets the second dimension of delay and timeOut to 1.

Note

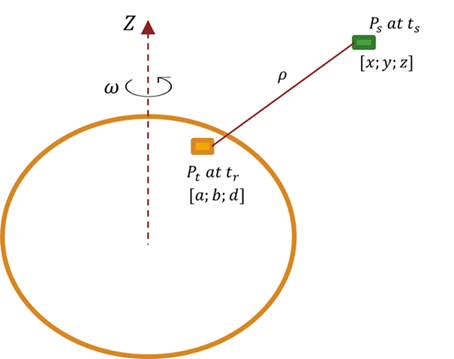
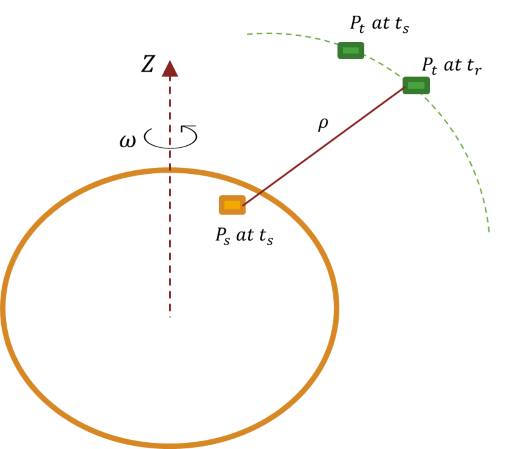
When the target asset is a Satellite object, the latency function uses a numerical iterative solution to compute the propagation delay. When the target asset is a GroundStation object, the latency function applies Sagnac correction to compute the propagation delay.

Examples

collapse all

Determine Propagation Delay

Open Live Script

Determine the history of propagation delay from a satellite to a ground station. Also, determine the corresponding time samples.

Create a satelliteScenario object.

startTime = datetime(2022,8,21);                       % August 21, 2022, 12:00 AM UTC
stopTime = datetime(2022,8,23);                        % August 23, 2022, 12:00 AM UTC
sampleTime = 60;                                       % Units are in seconds
sc = satelliteScenario(startTime,stopTime,sampleTime);

Add a satellite to the scenario.

semiMajorAxis = 10000000;             % In meters
eccentricity = 0;
inclination = 0;                      % In degrees
rightAscensionOfAscendingNode = 0;    % In degrees
argumentOfPeriapsis = 0;              % In degrees
trueAnomaly = 0;                      % In degrees
sat = satellite(sc,semiMajorAxis,eccentricity,inclination,rightAscensionOfAscendingNode,argumentOfPeriapsis,trueAnomaly);

Add a ground station to the scenario.

gs = groundStation(sc);

Determine the propagation delay history between two assets and the corresponding time samples.

[delay,timeOut] = latency(sat,gs);

Input Arguments

collapse all

`source` — Source asset from scenario
`Satellite` object | `GroundStation` object | `Platform` object | array of `Satellite` objects | array of `GroundStation` objects | array of `Platform` objects

Source asset from scenario, specified as a Satellite object, Platform object, GroundStation object, array of Satellite objects, array of Platform objects, or array of GroundStation objects.

`target` — Target asset from scenario
`Satellite` object | `GroundStation` object | `Platform` object | array of `Satellite` objects | array of `GroundStation` objects | array of `Platform` objects

Target asset from scenario, specified as a Satellite object, Platform object, GroundStation object, array of Satellite objects, array of Platform objects, or array of GroundStation objects.

`timeIn` — Time instance at which function calculates latency
datetime scalar

Time instance at which the function calculates latency, specified as a datetime scalar. If timeIn does not specify a time zone, the function uses Coordinated Universal Time (UTC).

Data Types: datetime

Output Arguments

collapse all

`delay` — History of propagation delay
scalar | vector | matrix

Delay, in seconds, returned as a scalar, vector, or matrix. When source and target cannot access each other, the corresponding latency value is NaN. These tables show how this output changes based on the different input argument sizes and combinations.

timeIn not specified

`source`	`target`	`delay`	Description
scalar	scalar	row vector	Latency history, in which each element represents the propagation delay from `source` to `target` at a specific time.
scalar	vector	matrix	Each row represents the propagation delay from `source` to `target`. The row index indicates the position of the asset in `target`.
vector	scalar	matrix	Each row represents the propagation delay from `source` to `target`. The row index indicates the position of the asset in `source`.
vector	vector	matrix	Each row represents the propagation delay from `source` to `target`. The row index indicates the position of the assets in `source` and `target`.

timeIn specified

`source`	`target`	`delay`	Description
scalar	scalar	scalar	Latency at the specified datetime `timeIn`.
scalar	vector	column vector	Each element represents the propagation delay from `source` to the corresponding asset in `target` at the specified datetime `timeIn`.
vector	scalar	column vector	Each element represents the propagation delay from the corresponding asset in `source` to `target` at the specified datetime `timeIn`.
vector	vector	column vector	Each element represents the propagation delay between the corresponding pair of `source` and `target` assets at the specified datetime `timeIn`.

Data Types: double

`timeOut` — Time samples between start and stop time of scenario
datetime vector | datetime scalar

Time samples between the start and stop time of the scenario, returned as a scalar or vector.

If timeIn does not specify a time zone and the AutoSimulate property the satelliteScenario object is true, the latency function returns the time sample history from StartTime to StopTime. Otherwise, it returns the time sample history from the value of StartTime to the value of SimulationTime.

Data Types: datetime

More About

collapse all

Latency When Ground Station Is Target

Consider a satellite scenario in which a satellite is the source and a ground station on Earth is the target. Because the satellite scenario currently supports only static ground stations, assume that the velocity of the ground station is the same as the angular velocity of Earth.

Given the instant at which the source transmits the signal $t_{s}$ and the instant at which the target receives the signal $t_{r}$ , the latency or propagation delay is the difference $t_{r} - t_{s}$ . Assume that at every instant, the source transmits the signal. The unknown is the instant at which the signal reaches the target.

Consider that the positions of the source and the target are in International Terrestrial Reference Frame (ITRF).

Source position P_s at t_s— ${[x y z]}^{'}$
Target position P_t at t_r — ${[a, b, d]}^{'}$

The distance between the target position P_t and the source position P_s in the t_r time frame is the distance travelled by the signal $ρ$ , where $ρ = ‖ P_{t}^{t_{r}} - P_{s}^{t_{r}} ‖ .$

To obtain the source position in the t_r time frame, apply this rotation matrix to the source position.

$R_{t_{s}}^{t_{r}} = [\begin{matrix} \cos (ω (t_{r} - t_{s})) & \sin (ω (t_{r} - t_{s})) & 0 \\ - \sin (ω (t_{r} - t_{s})) & \cos (ω (t_{r} - t_{s})) & 0 \\ 0 & 0 & 1 \end{matrix}]$

In this equation, the time difference $t_{r} - t_{s}$ equals the time taken by the signal to cover the distance $ρ$ .

$∴ t_{r} - t_{s} = \frac{ρ}{c} .$

Substitute this value in the rotation matrix to obtain

$R_{t_{s}}^{t_{r}} = [\begin{matrix} \cos (ω \frac{ρ}{c}) & \sin (ω \frac{ρ}{c}) & 0 \\ - \sin (ω \frac{ρ}{c}) & \cos (ω \frac{ρ}{c}) & 0 \\ 0 & 0 & 1 \end{matrix}] .$

The position of source in the time frame t_r is

$P_{s}^{t_{r}} = R_{t_{s}}^{t_{r}} P_{s}^{t_{s}} .$

$∴ P_{s}^{t_{r}} = [\begin{matrix} \cos (ω \frac{ρ}{c}) & \sin (ω \frac{ρ}{c}) & 0 \\ - \sin (ω \frac{ρ}{c}) & \cos (ω \frac{ρ}{c}) & 0 \\ 0 & 0 & 1 \end{matrix}] * [\begin{matrix} x \\ y \\ z \end{matrix}] .$

In this equation,

$ω$ is to the order of 1e-5.
$ρ$ is to the order of 1e7.
c is to the order of 1e-8.
$ω \frac{ρ}{c}$ is to the order of 1e-5.

As $ω \frac{ρ}{c}$ is very small, apply small angle approximation ( $\sin (θ) \approx θ$ and $\cos (θ) \approx 1$ ) to obtain

$P_{s}^{t_{r}} = [\begin{matrix} 1 & ω \frac{ρ}{c} & 0 \\ - ω \frac{ρ}{c} & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] * [\begin{matrix} x \\ y \\ z \end{matrix}] .$

Substitute this value in $ρ = ‖ P_{t}^{t_{r}} - P_{s}^{t_{r}} ‖$ to obtain

$ρ = \sqrt{{((x - a) + y ω \frac{ρ}{c})}^{2} + {(- x ω \frac{ρ}{c} + (y - b))}^{2} + {(z - d)}^{2}} .$

Square both sides of this equation to obtain

$ρ^{2} = ({(x - a)}^{2} + {(y ω \frac{ρ}{c})}^{2} + 2 (x - a) (y ω \frac{ρ}{c})) + ({(y - b)}^{2} + {(x ω \frac{ρ}{c})}^{2} - 2 (y - b) (x ω \frac{ρ}{c})) + {(z - d)}^{2} .$

Rearrange the terms and simplify the equation to obtain

$ρ^{2} = {(x - a)}^{2} + {(y - b)}^{2} + {(z - d)}^{2} + ({(ω \frac{ρ}{c})}^{2} (x^{2} + y^{2}) + 2 ω \frac{ρ}{c} (b x - a y)) .$

The true geometric range for the position of source and target in the t_r time frame is

$r^{2} = ({(a - x)}^{2} + {(b - y)}^{2} + {(d - z)}^{2}) .$

Let $R_{corr} = \frac{ω}{c} (b x - a y)$ and $e_{1}^{'} = {(\frac{ω}{c})}^{2} (x^{2} + y^{2})$ . Substitute these values in $ρ^{2} = {(x - a)}^{2} + {(y - b)}^{2} + {(z - d)}^{2} + ({(ω \frac{ρ}{c})}^{2} (x^{2} + y^{2}) + 2 ω \frac{ρ}{c} (b x - a y))$ to obtain

$ρ^{2} = r^{2} + (e_{1}^{'} ρ^{2} + 2 ρ R_{corr}) .$

$∴ (1 - e_{1}^{'}) ρ^{2} - 2 ρ R_{corr} - r^{2} = 0.$

The discriminant of this quadratic equation is

$d i s c r i m i n a n t = 4 R_{corr}^{2} + 4 (1 - e_{1}^{'}) r^{2} .$

$∴ ρ = \frac{2 R_{corr} + \sqrt{d i s c r i m i n a n t}}{2 (1 - e_{1}^{'})} .$

If $R_{corr} ≪ r \sqrt{(1 - e_{1}^{'})}$ , then you can express $ρ$ as

$ρ = \frac{2 R_{corr} + 2 r \sqrt{1 - e_{1}^{'}}}{2 (1 - e_{1}^{'})} = \frac{R_{corr}}{(1 - e_{1}^{'})} + \frac{r}{\sqrt{1 - e_{1}^{'}}} .$

Latency When Satellite Is Target

When the target is a satellite, you must consider the movement of a satellite to know when the satellite receives the signal.

Let f be the function that defines the orbital motion of the satellite, which is nonlinear with no sharp peaks. Also, let P_S be the position of the source in Geocentric Celestial Reference Frame (GCRF). The time taken by the signal to reach the target equals the time the target takes to move from its position at the transmission time to its position at the reception time.

You can find the solution for the objective function iteratively by using the Newton-Raphson method.

$O b j e c t i v e F u n c t i o n (t) = (\frac{‖ f (t_{S} + t) - P_{S} ‖}{c}) - t$ , where t_S is the source transmit time.

Assuming the satellite does not move, the initial guess to the function is the time the signal takes to reach the satellite.

The root of the objective function is latency. Obtaining the exact root is not always possible because of the numerical precision errors. Therefore, consider the value for which the objective function returns a value less than 2.2204e-16 as the root.

This methodology is applicable for any moving target, regardless of source movement.

Version History

Introduced in R2023a

latency

Syntax

Description

Examples

Determine Propagation Delay

Input Arguments

`source` — Source asset from scenario
`Satellite` object | `GroundStation` object | `Platform` object | array of `Satellite` objects | array of `GroundStation` objects | array of `Platform` objects

`target` — Target asset from scenario
`Satellite` object | `GroundStation` object | `Platform` object | array of `Satellite` objects | array of `GroundStation` objects | array of `Platform` objects

`timeIn` — Time instance at which function calculates latency
datetime scalar

Output Arguments

`delay` — History of propagation delay
scalar | vector | matrix

`timeOut` — Time samples between start and stop time of scenario
datetime vector | datetime scalar

More About

Latency When Ground Station Is Target

Latency When Satellite Is Target

Version History

See Also

Objects

Functions

Topics

latency

Syntax

Description

Examples

Determine Propagation Delay

Input Arguments

source — Source asset from scenario Satellite object | GroundStation object | Platform object | array of Satellite objects | array of GroundStation objects | array of Platform objects

target — Target asset from scenario Satellite object | GroundStation object | Platform object | array of Satellite objects | array of GroundStation objects | array of Platform objects

timeIn — Time instance at which function calculates latency datetime scalar

Output Arguments

delay — History of propagation delay scalar | vector | matrix

timeOut — Time samples between start and stop time of scenario datetime vector | datetime scalar

More About

Latency When Ground Station Is Target

Latency When Satellite Is Target

Version History

See Also

Objects

Functions

Topics

`source` — Source asset from scenario
`Satellite` object | `GroundStation` object | `Platform` object | array of `Satellite` objects | array of `GroundStation` objects | array of `Platform` objects

`target` — Target asset from scenario
`Satellite` object | `GroundStation` object | `Platform` object | array of `Satellite` objects | array of `GroundStation` objects | array of `Platform` objects

`timeIn` — Time instance at which function calculates latency
datetime scalar

`delay` — History of propagation delay
scalar | vector | matrix

`timeOut` — Time samples between start and stop time of scenario
datetime vector | datetime scalar