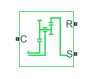
Compound Planetary Gear

Planetary gear train with stepped planet gear set

Libraries:
Simscape / Driveline / Gears

Description

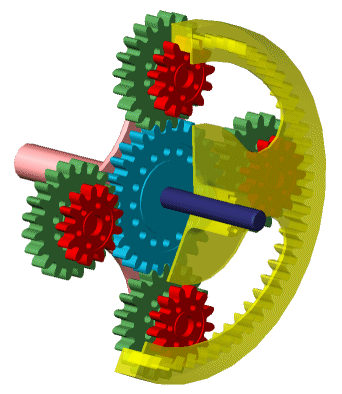
The Compound Planetary Gear block represents a planetary gear train with composite planet gears. Each composite planet gear is a pair of rigidly connected and longitudinally arranged gears of different radii. One of the two gears engages the centrally located sun gear while the other engages the outer ring gear.

Compound Planetary Gear

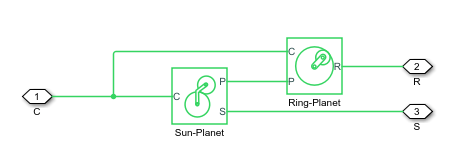
The block models the compound planetary gear as a structural component based on the Simscape™ Driveline™ Sun-Planet and Ring-Planet blocks. The figure demonstrates the equivalent block diagram for the Compound planetary gear block.

To increase the fidelity of the gear model, specify properties such as gear inertia, meshing losses, and viscous losses. By default, gear inertia and viscous losses are assumed to be negligible. The block enables you to specify the inertias of the internal planet gears. To model the inertias of the carrier, sun, and ring gears, connect Simscape Inertia blocks to ports C, S, and R.

Thermal Model

You can model the effects of heat flow and temperature change by enabling the optional thermal port. To enable the port, set Friction model to Temperature-dependent efficiency.

Equations

Ideal Gear Constraints and Gear Ratios

The Compound Planetary Gear block imposes two kinematic and two geometric constraints.

$r_{C} ω_{C} = r_{S} ω_{S} + r_{P 1} ω_{P},$

$r_{R} ω_{R} = r_{C} ω_{C} + r_{P 2} ω_{P},$

$r_{C} = r_{S} + r_{P 1},$

$r_{R} = r_{C} + r_{P 2},$

where:

r_C is the radius of the carrier gear.
ω_C is the angular velocity of the carrier gear.
r_S is the radius of the sun gear.
ω_S is the angular velocity of the sun gear.
r_P1 is the radius of planet gear 1.
ω_P is the angular velocity of the planet gears.
r_P2 is the radius of planet gear 2.
r_R is the radius of the ring gear.

The ring-planet and planet-sun gear ratios are:

$g_{R P} = r_{R} / r_{P 2} = N_{R} / N_{P 2}$

and

$g_{P S} = r_{P 1} / r_{S} = N_{P 1} / N_{S},$

where:

g_RP is the ring-planet gear ratio.
N_R is the number of teeth on the ring gear.
N_P2 is the number of teeth on planet gear 2.
g_PS is the planet-sun gear ratio.
N_P1 is the number of teeth on planet gear 1.
N_S is the number of teeth on the sun gear.

In terms of the gear ratios, the key kinematic constraint is:

$(1 + g_{R P} g_{P S}) ω_{C} = ω_{S} + g_{R P} g_{P S} ω_{R} .$

The four degrees of freedom reduce to two independent degrees of freedom. The gear pairs are (1, 2) = (P2, R) and (S, P1).

Warning

The gear ratio g_RP must be strictly greater than one.

The torque transfers are:

$g_{R P} τ_{P 2} + τ_{R} - τ_{l o s s} (P 2, R) = 0$

and

$g_{P S} τ_{S} + τ_{P 1} - τ_{l o s s} (S, P 1) = 0,$

where:

τ_P2 is torque transfer for planet gear 2.
τ_R is torque transfer for the ring gear.
τ_loss is torque transfer loss.
τ_S is torque transfer for the sun gear.
τ_P1 is torque transfer for planet gear 1.

In the ideal case where there is no torque loss, τ_loss = 0.

Nonideal Gear Constraints and Losses

In the nonideal case, τ_loss ≠ 0. For more information, see Model Gears with Losses.

Assumptions and Limitations

Gear inertia is assumed to be negligible.
Gears are treated as rigid components.
Coulomb friction slows down simulation. For more information, see Adjust Model Fidelity.

Ports

Conserving

expand all

C — Planet gear carrier
rotational mechanical

Rotational mechanical conserving port associated with the planet gear carrier.

R — Ring gear
rotational mechanical

Rotational mechanical conserving port associated with the ring gear.

S — Sun gear
rotational mechanical

Rotational mechanical conserving port associated with the sun gear.

H — Heat flow
thermal

Thermal conserving port associated with heat flow. Heat flow affects the power transmission efficiency by altering the gear temperatures.

Dependencies

To enable this port, set Friction model to Temperature-dependent efficiency.

Parameters

expand all

Main

Ring (R) to planet (P) teeth ratio (NR/NP) — Ring to planet gear rotation ratio
`2` (default) | scalar greater than `1`

Fixed ratio, g_RP, of the ring gear to the planet gear rotations as defined by the number of ring gear teeth divided by the number of planet gear teeth. This gear ratio must be strictly greater than 1.

Planet (P) to sun (S) teeth ratio (NP/NS) — Planet to sun gear rotation ratio
`1` (default) | positive scalar

Fixed ratio, g_PS, of the planet gear to the sun gear rotations as defined by the number of planet gear teeth divided by the number of sun gear teeth. This gear ratio must be strictly greater than 0.

Meshing Losses

Friction model — Friction model
`No meshing losses - Suitable for HIL simulation` (default) | `Constant efficiency` | `Temperature-dependent efficiency`

Friction model for the block:

No meshing losses - Suitable for HIL simulation — Gear meshing is ideal.
Constant efficiency — Transfer of torque between the gear wheel pairs is reduced by a constant efficiency, η, such that 0 < η ≤ 1.
Temperature-dependent efficiency — Transfer of torque between the gear wheel pairs is defined by the table lookup based on the temperature.

Sun-planet and ring-planet ordinary efficiencies — Torque transfer efficiencies
`[.96 .98]` (default) | vector

Vector of torque transfer efficiencies, [η_SP η_RP], for sun-planet and ring-carrier gear wheel pair meshings, respectively. The vector element must be in the interval (0,1].

Dependencies

To enable this parameter, set Friction model to Constant efficiency.

Temperature — Temperature
`[280, 300, 320]` `K` (default) | vector

Vector of temperatures used to construct a 1-D temperature-efficiency lookup table. The vector elements must increase from left to right.

Dependencies

To enable this parameter, set Friction model to Temperature-dependent efficiency.

Sun-planet efficiency — Sun-planet efficiency
`[.95, .9, .85]` (default) | vector | rot

Vector of output-to-input power ratios that describe the power flow from the sun gear to the planet gear, η_SP. The block uses the values to construct a 1-D temperature-efficiency lookup table.

Each element is an efficiency that relates to a temperature in the Temperature vector. The length of the vector must be equal to the length of the Temperature vector. Each element in the vector must be in the range (0,1].

Dependencies

To enable this parameter, set Friction model to Temperature-dependent efficiency.

Ring-planet efficiency — Ring-planet efficiency
`[.95 .9 .85]` (default) | vector

Vector of component efficiencies, η_RP—the ratio of output power to input power, that the block uses to construct a 1-D temperature-efficiency lookup table.

Dependencies

To enable this parameter, set Friction model to Temperature-dependent efficiency.

Sun-carrier and planet-carrier power thresholds — Minimum efficiency power threshold for the sun-carrier and planet carrier gear couplings
`[.001, .001]` `W` (default) | vector

Vector of power thresholds above which the full efficiency factors apply. Enter the thresholds in the order sun-carrier, planet-carrier. Below these values, a hyperbolic tangent function smooths the efficiency factor.

When you set Friction model to Constant efficiency, the block lowers the efficiency losses to zero when no power is transmitted. When you set Friction model to Temperature-dependent efficiency, the block smooths the efficiency factors between zero when at rest and the values provided by the temperature-efficiency lookup tables at the power thresholds.

Dependencies

To enable this parameter, set Friction model to Constant efficiency or Temperature-dependent efficiency.

Viscous Losses

Sun-carrier and planet-carrier viscous friction coefficients — Gear viscous friction
`[0 0]` `N*m/(rad/s)` (default) | vector

Vector of viscous friction coefficients, [μ_S μ_P], for the sun-carrier and planet-carrier gear motions, respectively.

Inertia

Inertia — Inertia model
`off` (default) | `on`

Inertia model for the block:

Off — Model gear inertia.
On — Neglect gear inertia.

Sun gear inertia — Sun gear inertia
`0.001` `kg*m^2` (default) | positive scalar

Sun gear inertia.

Dependencies

To enable this parameter, set Inertia to On.

Ring gear inertia — Ring gear inertia
`0.001` `kg*m^2` (default) | positive scalar

Ring gear inertia.

Dependencies

To enable this parameter, set Inertia to On.

Carrier gear inertia — Carrier gear inertia
`0.001` `kg*m^2` (default) | positive scalar

Carrier gear inertia.

Dependencies

To enable this parameter, set Inertia to On.

Carrier gear radius — Carrier gear radius
`0.01` `m` (default) | positive scalar

Carrier gear radius.

Dependencies

To enable this parameter, set Inertia to On.

Planet gear spin inertia — Planet gear spin inertia
`0.001` `kg*m^2` (default) | positive scalar

Planetary gear inertia about its own axis.

Dependencies

To enable this parameter, set Inertia to On.

Planet gear mass — Planet gear mass
`0.001` `kg*m^2` (default) | positive scalar

Planet gear mass.

Dependencies

To enable this parameter, set Inertia to On.

Thermal Port

To enable this parameter, set Friction model to Temperature-dependent efficiency.

Thermal mass — Thermal mass
`50` `J/K` (default) | scalar

Thermal energy required to change the component temperature by a single temperature unit. The greater the thermal mass, the more resistant the component is to temperature change.

Dependencies

To enable this parameter, set Friction model to Temperature-dependent efficiency.

Initial temperature — Initial temperature
`300` `K` (default) | scalar

Block temperature at the start of simulation. The initial temperature sets the initial component efficiencies according to their respective efficiency vectors.

Dependencies

To enable this parameter, set Friction model to Temperature-dependent efficiency.

More About

expand all

Hardware-in-the-Loop Simulation

For optimal simulation performance, set Friction model to the default value, No meshing losses - Suitable for HIL simulation.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2011a

expand all

R2024b: Inertia updates

You now can specify the inertia of all gear subcomponents including the sun, ring, and carrier gears. You also now can include the effects of planet procession in the planet inertia behavior.

Compound Planetary Gear

Description

Thermal Model

Equations

Assumptions and Limitations

Ports

Conserving

C — Planet gear carrier rotational mechanical

R — Ring gear rotational mechanical

S — Sun gear rotational mechanical

H — Heat flow thermal

Dependencies

Parameters

Main

Ring (R) to planet (P) teeth ratio (NR/NP) — Ring to planet gear rotation ratio 2 (default) | scalar greater than 1

Planet (P) to sun (S) teeth ratio (NP/NS) — Planet to sun gear rotation ratio 1 (default) | positive scalar

Meshing Losses

Friction model — Friction model No meshing losses - Suitable for HIL simulation (default) | Constant efficiency | Temperature-dependent efficiency

Sun-planet and ring-planet ordinary efficiencies — Torque transfer efficiencies [.96 .98] (default) | vector

Dependencies

Temperature — Temperature [280, 300, 320] K (default) | vector

Dependencies

Sun-planet efficiency — Sun-planet efficiency [.95, .9, .85] (default) | vector | rot

Dependencies

Ring-planet efficiency — Ring-planet efficiency [.95 .9 .85] (default) | vector

Dependencies

Sun-carrier and planet-carrier power thresholds — Minimum efficiency power threshold for the sun-carrier and planet carrier gear couplings [.001, .001] W (default) | vector

Dependencies

Viscous Losses

Sun-carrier and planet-carrier viscous friction coefficients — Gear viscous friction [0 0] N*m/(rad/s) (default) | vector

Inertia

Inertia — Inertia model off (default) | on

Sun gear inertia — Sun gear inertia 0.001 kg*m^2 (default) | positive scalar

Dependencies

Ring gear inertia — Ring gear inertia 0.001 kg*m^2 (default) | positive scalar

Dependencies

Carrier gear inertia — Carrier gear inertia 0.001 kg*m^2 (default) | positive scalar

Dependencies

Carrier gear radius — Carrier gear radius 0.01 m (default) | positive scalar

Dependencies

Planet gear spin inertia — Planet gear spin inertia 0.001 kg*m^2 (default) | positive scalar

Dependencies

Planet gear mass — Planet gear mass 0.001 kg*m^2 (default) | positive scalar

Dependencies

Thermal Port

Thermal mass — Thermal mass 50 J/K (default) | scalar

Dependencies

Initial temperature — Initial temperature 300 K (default) | scalar

Dependencies

More About

Hardware-in-the-Loop Simulation

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2024b: Inertia updates

See Also

Simscape Blocks

Topics

C — Planet gear carrier
rotational mechanical

R — Ring gear
rotational mechanical

S — Sun gear
rotational mechanical

H — Heat flow
thermal

Ring (R) to planet (P) teeth ratio (NR/NP) — Ring to planet gear rotation ratio
`2` (default) | scalar greater than `1`

Planet (P) to sun (S) teeth ratio (NP/NS) — Planet to sun gear rotation ratio
`1` (default) | positive scalar

Friction model — Friction model
`No meshing losses - Suitable for HIL simulation` (default) | `Constant efficiency` | `Temperature-dependent efficiency`

Sun-planet and ring-planet ordinary efficiencies — Torque transfer efficiencies
`[.96 .98]` (default) | vector

Temperature — Temperature
`[280, 300, 320]` `K` (default) | vector

Sun-planet efficiency — Sun-planet efficiency
`[.95, .9, .85]` (default) | vector | rot

Ring-planet efficiency — Ring-planet efficiency
`[.95 .9 .85]` (default) | vector

Sun-carrier and planet-carrier power thresholds — Minimum efficiency power threshold for the sun-carrier and planet carrier gear couplings
`[.001, .001]` `W` (default) | vector

Sun-carrier and planet-carrier viscous friction coefficients — Gear viscous friction
`[0 0]` `N*m/(rad/s)` (default) | vector

Inertia — Inertia model
`off` (default) | `on`

Sun gear inertia — Sun gear inertia
`0.001` `kg*m^2` (default) | positive scalar

Ring gear inertia — Ring gear inertia
`0.001` `kg*m^2` (default) | positive scalar

Carrier gear inertia — Carrier gear inertia
`0.001` `kg*m^2` (default) | positive scalar

Carrier gear radius — Carrier gear radius
`0.01` `m` (default) | positive scalar

Planet gear spin inertia — Planet gear spin inertia
`0.001` `kg*m^2` (default) | positive scalar

Planet gear mass — Planet gear mass
`0.001` `kg*m^2` (default) | positive scalar

Thermal mass — Thermal mass
`50` `J/K` (default) | scalar

Initial temperature — Initial temperature
`300` `K` (default) | scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.