倒频谱分析
什么是倒频谱?
倒频谱分析是一种非线性信号处理方法,在语音和图像处理等领域有多种应用。
序列 x 的复倒频谱是通过求 x 的傅里叶变换的复自然对数,然后对得到的序列进行傅里叶逆变换来计算的:
工具箱函数 cceps 执行此运算,估计输入序列的复倒频谱。它返回与输入序列大小相同的实数序列。
您可以在回声检测应用程序中使用 cceps 函数。首先,创建以 100 Hz 采样的 45 Hz 正弦波。在信号开始 0.2 秒后,添加一个振幅减半的回声。
t = 0:0.01:1.27; s1 = sin(2*pi*45*t); s2 = s1 + 0.5*[zeros(1,20) s1(1:108)];
计算并绘制新信号的复倒频谱。
c = cceps(s2); plot(t,c)
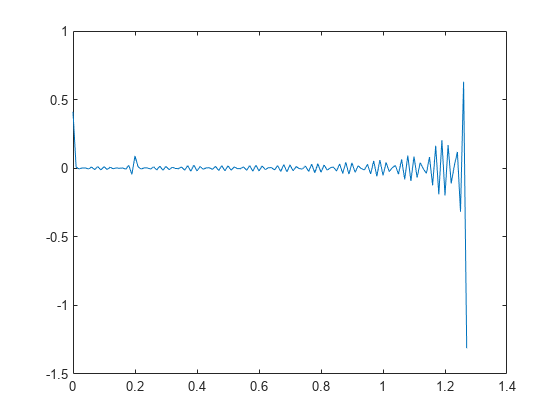
复倒频谱显示在 0.2 秒处出现一个峰值,指示该回声。
信号 x 的实倒频谱,有时直接称为倒频谱,是通过确定 x 的傅里叶变换的幅值的自然对数,然后获取所得序列的傅里叶逆变换来计算的:
工具箱函数 rceps 执行此运算,返回序列的实倒频谱。返回的序列是与输入向量大小相同的实数值向量。
rceps 函数还返回唯一的最小相位序列,该序列具有与输入相同的实倒频谱。要同时求得一个序列的实倒频谱和最小相位重构,请使用 [y,ym] = rceps(x),其中 y 是实倒频谱,ym 是 x 的最小相位重构。以下示例显示 rceps 的输出之一是一个唯一的最小相位序列,其实倒频谱与 x 相同。
y = [4 1 5]; % Non-minimum phase sequence
[xhat,yhat] = rceps(y);
xhat2 = rceps(yhat);
[xhat' xhat2']ans = 3×2
1.6225 1.6225
0.3400 0.3400
0.3400 0.3400
对复倒频谱求逆
要对复倒频谱求逆,请使用 icceps 函数。求逆过程相当复杂,因为 cceps 函数执行数据相关相位修正,使其输入的展开相位在零频率处是连续的。相位修正等效于整数延迟。如果您增加第二个输出,cceps 将返回此延迟项:
x = 1:10; [xhat,delay] = cceps(x)
xhat = 1×10
2.2428 -0.0420 -0.0210 0.0045 0.0366 0.0788 0.1386 0.2327 0.4114 0.9249
delay = 1
要对复倒频谱求逆,请使用 icceps 和原始延迟参数:
icc = icceps(xhat,2)
icc = 1×10
2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 10.0000 1.0000
如以上示例所示,对复倒频谱进行任何修正后,原始延迟项可能不再有效。您将无法精确地对复倒频谱求逆。