多通道输入的互相关

R2026b

生成三个包含 11 个样本的指数序列，这些样本由 $0 . 4^{n}$ 、 $0 . 7^{n}$ 和 $0.99 9^{n}$ ( $n \geq 0$ ) 给出。使用 stem3 并排绘制这些序列。

N = 11;
n = (0:N-1)';

a = 0.4;
b = 0.7;
c = 0.999;

xabc = [a.^n b.^n c.^n];

stem3(n,1:3,xabc',"filled")
ax = gca;
ax.YTick = 1:3;
view(37.5,30)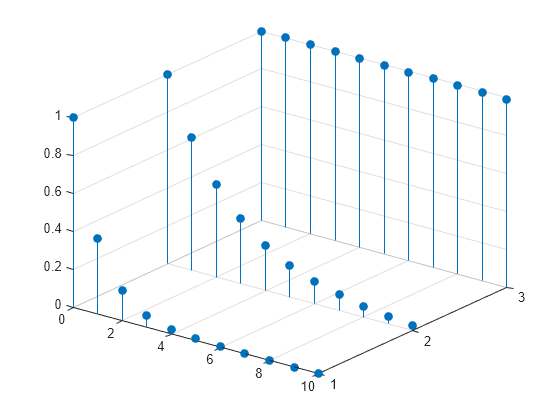

Figure contains an axes object. The axes object contains an object of type stem.

计算这些序列的自相关和互相关。输出滞后，这样您就不必跟踪它们。将结果归一化，使自相关在零滞后处具有单位值。

[cr,lgs] = xcorr(xabc,"coeff");

tiledlayout(3,3,TileSpacing="tight")
for row = 1:3
    for col = 1:3
        nm = 3*(row-1)+col;
        nexttile
        stem(lgs,cr(:,nm),".")
        title("c_{" + row + col  + "}")
        ylim([0 1])
    end
end

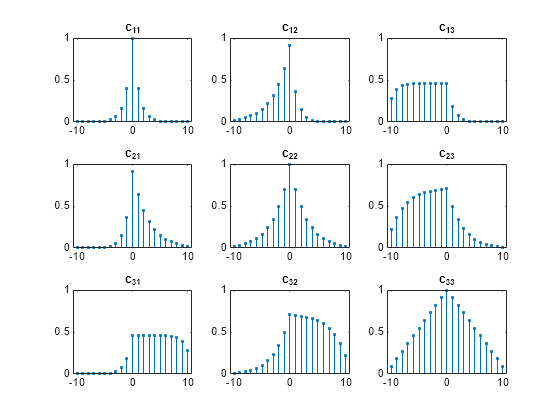
仅计算滞后值为 $- 5$ 和 $5$ 之间时的相关性。

[cr,lgs] = xcorr(xabc,5,"coeff");

tiledlayout(3,3,TileSpacing="tight")
for row = 1:3
    for col = 1:3
        nm = 3*(row-1)+col;
        nexttile
        stem(lgs,cr(:,nm),".")
        title("c_{" + row + col  + "}")
        ylim([0 1])
    end
end

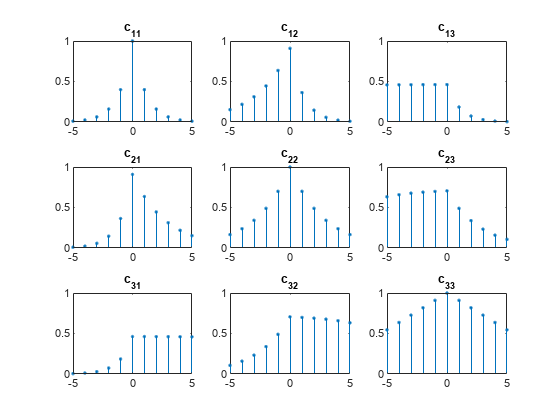
计算自相关和互相关性无偏估计。默认情况下，滞后介于 $- (N - 1)$ 和 $N - 1$ 之间。

cu = xcorr(xabc,"unbiased");

tiledlayout(3,3,TileSpacing="tight")
for row = 1:3
    for col = 1:3
        nm = 3*(row-1)+col;
        nexttile
        stem(-(N-1):(N-1),cu(:,nm),".")
        title("c_{" + row + col  + "}")
    end
end

另请参阅

函数

xcorr