从生理信号中提取分类特征
此示例说明如何使用 midcross 和 dtw 函数从步态信号数据中提取特征。步态信号用于研究神经退行性疾病患者的行走模式。据报道,健康人和患者的步幅间隔时间不同。midcross 提供了一种方便的方法来计算这些时间。随着时间的推移,人们的行走速度也会发生变化。dtw 提供了一种方便的方法,通过畸变来定量比较步态信号的形状,以便在时间上对齐它们。此示例使用 midcross 定位步态信号中的每一步,并使用 dtw 计算步态信号段之间的距离。这些结果被视为信号分类的潜在特征。虽然此示例专用于步态信号,但也可以使用这些函数来分析其他生理信号,例如心电图 (ECG) 或光电血管容积图 (PPG) 信号。
测量步幅间时间间隔
要分析的数据集包含收集的肌萎缩侧索硬化症 (ALS) 患者和对照组在行走过程中的力数据。患有 ALS 的名人有卢伽雷和斯蒂芬·霍金,该疾病因 2014 年“冰桶挑战”而广受关注。
加载并绘制一名患者的前 30 秒步态信号数据。
helperGaitPlot("als1m");
xlim([0 30])
此数据集表示脚施加在力敏感电阻器上的力。力以毫伏为单位测量。每次记录长度为一分钟,包含受试者左右脚的独立通道数据。数据集中的每一步都以脚接触地面和离开地面时力的急剧变化为特征。使用 midcross 为 ALS 患者找到这些急剧变化。
使用 midcross 查找并绘制 ALS 患者左脚的每个过中值点的位置。选择 25% 的容差,以确保检测到每个过中值点。
Fs = 300; gaitSignal = helperGaitImport("als1m"); midcross(gaitSignal(1,:),Fs,Tolerance=25); xlim([0 30]) xlabel("Sample Number") ylabel("mV")
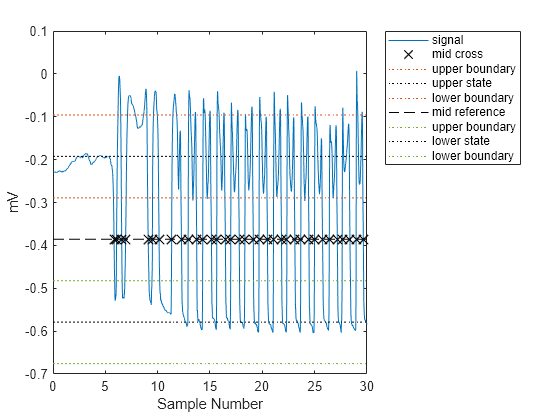
midcross 正确识别过中值点。现在用它来计算一组(包含 10 个)患者的步幅间时间。其中 5 个人作为对照受试者,另外 5 个是 ALS 患者。使用每个患者的左脚记录,排除前八个过中值点以消除瞬变。
pnames = helperGaitImport(); for i = 1:10 gaitSignal = helperGaitImport(pnames{i}); IND2 = midcross(gaitSignal(1,:),Fs,Tolerance=25); IST{i} = diff(IND2(9:2:end)); varIST(i) = var(IST{i}); end
绘制步幅间时间。
figure hold on for i = 1:5 plot(1:length(IST{i}),IST{i},".-") plot(1:length(IST{i+5}),IST{i+5},".-") end xlabel("Stride Number") ylabel("Time Between Strides (seconds)") legend("ALS","Control")

总的来说,ALS 患者的步幅间时间的方差更大。
测量行走模式的相似性
量化步间距离后,独立于这些步间的差异来分析步态信号数据的形状。使用 dtw 比较信号的两个段。理想情况下,随着治疗或疾病的进展,人们会比较步态信号的形状。此处,我们比较同一记录的两个段,一个段在记录的早期 (sigsInitialLeft),第二个段在接近结束位置 (sigsFinalLeft)。每个段包含六步。
加载步态信号数据段。
load PNGaitSegments.mat在整个记录中,患者走路的速度不同。dtw 通过对这些段进行畸变处理使其在时间上对齐,来测量段之间的距离。使用 dtw 比较这两个段。
figure
dtw(sigsInitialLeft{1},sigsFinalLeft{1});
legend("Early segment","Later segment",Location="southeast")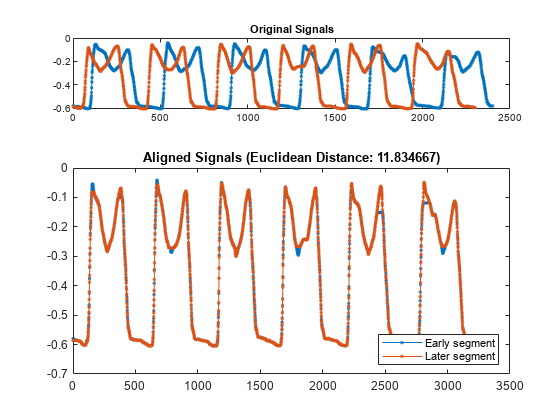
这两个段在时间上是对齐的。虽然患者的步速显示为随时间而变化,但从原始信号的偏移可以看出,dtw 通过允许任一段的采样重复来匹配两个段。通过 dtw 得到的距离,以及步幅间时间的方差,将作为步态信号分类器的特征进行研究。
构造特征向量以对信号进行分类
假设您要构建一个分类器,以根据步态信号来判断患者是否健康。调查步幅间时间的方差(即 feature1)和通过 dtw 得到的初始信号段和最终信号段之间的距离(即 feature2),将其作为分类特征。
特征 1 是先前使用 midcross 计算的。
feature1 = varIST;
为 ALS 患者和对照组提取特征 2。
feature2 = zeros(10,1); for i = 1:length(sigsInitialLeft) feature2(i) = dtw(sigsInitialLeft{i},sigsFinalLeft{i}); end
绘制 ALS 受试者和对照受试者的特征。
figure plot(feature1(1:5),feature2(1:5),"*",... feature1(6:10),feature2(6:10),"+",... MarkerSize=10,LineWidth=1) xlabel("Variance of Inter-Stride Times") ylabel("Distance Between Segments") legend("ALS","Control")
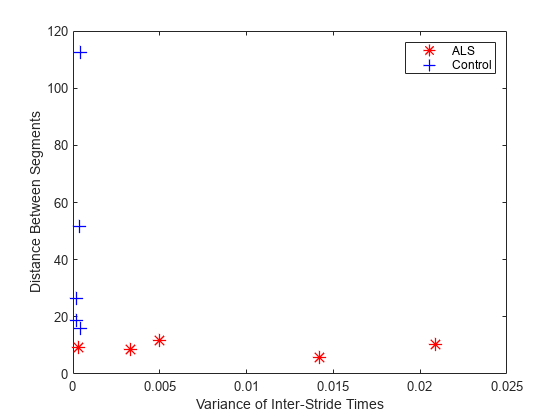
ALS 患者的步幅间时间的方差较大,但通过 dtw 得到的段间距离较小。这些特征相互补充,并可供研究以用于神经网络或支持向量机等分类器。
结论
midcross 和 dtw 提供了一种方便的方法来比较由于不同运动或活动速率而随时间不规则重复的步态信号和其他生理数据。在此示例中,我们使用了 midcross 来定位步时间,使用了 dtw 来计算段距离。这些是互补测量,因为 dtw 消除了 midcross 距离测量的任何时变。作为特征,这两个度量显示此数据集的对照受试者和 ALS 患者之间的不同。midcross 和 dtw 同样可用于检查形状随活动而变化的其他生理信号。
参考资料
[1] Goldberger, A. L., L. A. N. Amaral, L. Glass, J. M. Hausdorff, P. Ch.Ivanov, R. G. Mark, R. G. Mietus, G. B. Moody, C.-K. Peng, and H. E. Stanley."PhysioBank, PhysioToolkit, and PhysioNet:Components of a New Research Resource for Complex Physiologic Signals."Circulation.Vol. 101, Number 23, 2000, pp. e215-e200.