Main Content

希尔伯特变换

打开实时脚本

希尔伯特变换可用于形成解析信号。解析信号在通信领域中很有用，尤其是在带通信号处理中。工具箱函数 hilbert 计算实数输入序列 x 的希尔伯特变换，并返回相同长度的复数结果，即 y = hilbert(x)，其中 y 的实部是原始实数数据，虚部是实际希尔伯特变换。在涉及到连续时间解析信号时，y 有时被称为解析信号。离散时间解析信号的关键属性是它的 Z 变换在单位圆的下半部分为 0。解析信号的许多应用都与此属性相关；例如，用解析信号避免带通采样操作的混叠效应。解析信号的幅值是原始信号的复包络。

希尔伯特变换对实际数据作 90 度相移；正弦变为余弦，反之亦然。要绘制一部分数据及其希尔伯特变换，请使用

t = 0:1/1024:1;
x = sin(2*pi*60*t);
y = hilbert(x);

plot(t(1:50),real(y(1:50)))
hold on
plot(t(1:50),imag(y(1:50)))
hold off
axis([0 0.05 -1.1 2])
legend('Real Part','Imaginary Part')

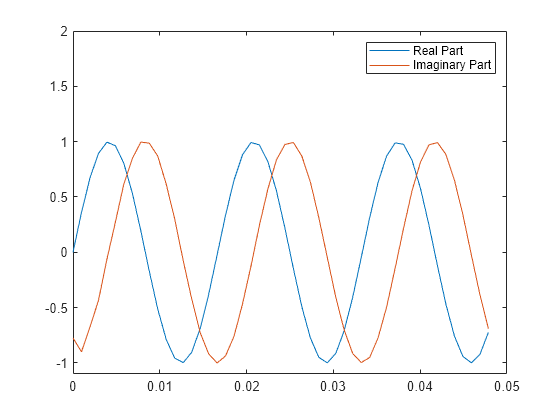
解析信号可用于计算时间序列的瞬时属性，即时间序列在任一时间点的属性。该过程要求信号是单分量的。

另请参阅

相关主题