线性和循环卷积
此示例说明如何建立线性卷积和循环卷积之间的等效关系。
线性卷积和循环卷积是本质不同的运算。然而,在某些条件下,线性卷积和循环卷积是等效的。建立这种等效关系具有重要意义。对于两个向量 x 和 y,循环卷积等于二者的离散傅里叶变换 (DFT) 之积的逆 DFT 变换。了解线性卷积和循环卷积等效的条件,可让您使用 DFT 来高效地计算线性卷积。
包含 N 个点的向量 x 和包含 L 个点的向量 y 的线性卷积长度为 N + L - 1。
为了使 x 和 y 的循环卷积与之等效,在进行 DFT 之前,必须用零填充向量,使长度至少为 N + L - 1。对 DFT 的积求逆后,只保留前 N + L - 1 个元素。
创建两个向量 x 和 y,并计算两个向量的线性卷积。
x = [2 1 2 1]; y = [1 2 3]; clin = conv(x,y);
输出长度为 4+3-1。
用 0 填充两个向量,使长度为 4+3-1。求出两个向量的 DFT,将其相乘,并求乘积的逆 DFT。
xpad = [x zeros(1,6-length(x))]; ypad = [y zeros(1,6-length(y))]; ccirc = ifft(fft(xpad).*fft(ypad));
填零后的向量 xpad 和 ypad 的循环卷积等效于 x 和 y 的线性卷积。保留 ccirc 的所有元素,因为输出长度为 4+3-1。
绘制线性卷积的输出和 DFT 之积的逆,以显示二者等效。
subplot(2,1,1) stem(clin,'filled') ylim([0 11]) title('Linear Convolution of x and y') subplot(2,1,2) stem(ccirc,'filled') ylim([0 11]) title('Circular Convolution of xpad and ypad')
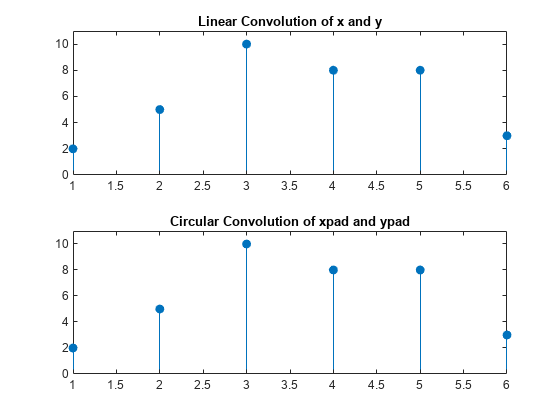
将向量填充到长度为 12,并使用 DFT 之积的逆 DFT 求得循环卷积。仅保留前 4+3-1 个元素,以产生与线性卷积等效的结果。
N = length(x)+length(y)-1; xpad = [x zeros(1,12-length(x))]; ypad = [y zeros(1,12-length(y))]; ccirc = ifft(fft(xpad).*fft(ypad)); ccirc = ccirc(1:N);
Signal Processing Toolbox™ 软件提供了函数 cconv,该函数返回两个向量的循环卷积。您可以通过以下代码使用循环卷积来求 x 和 y 的线性卷积。
ccirc2 = cconv(x,y,6);
cconv 内部使用的就是上例中基于 DFT 的步骤。