时频分析实践介绍
此示例说明如何执行和解释基本的时频信号分析。在实际应用中,许多信号是非平稳信号。这意味着其频域表示(其频谱)随时间变化。该示例讨论使用时频方法相对于信号的频域或时域表示的优势。它回答了一些基本问题,例如:信号中何时会出现特定频率分量?如何提高时间或频率分辨率?如何锐化分量的频谱或提取特定模式?如何在时频表示中测量功率?如何可视化信号的时频信息?如何在感兴趣信号的频率成分里找到间歇性干扰?
也可以使用连续小波变换来执行信号的时频分析。有关详细信息,请参阅Practical Introduction to Time-Frequency Analysis Using the Continuous Wavelet Transform (Wavelet Toolbox)。
使用时频分析识别 DTMF 信号中的数字
您可以将几乎任何时变信号划分为足够短的时间区间,这样,信号在每个区间内基本上是平稳的。通常,时频分析是通过将一个信号分割为若干短周期并在滑动窗内估计频谱来进行的。与 "spectrogram" 选项结合使用的 pspectrum 函数计算每个滑动窗内基于 FFT 的频谱估计值,让您直观地看到信号的频率成分如何随时间变化。
以某数字电话拨号的信号系统为例。这种系统产生的信号称为双音多频 (DTMF) 信号。每个拨号号码生成的声音由两个正弦波 即音调 的总和组成,频率取自两个互斥的组。每对音调包含一个低组频率(697 Hz、770 Hz、852 Hz 或 941 Hz)和一个高组频率(1209 Hz、1336 Hz 或 1477 Hz),并表示一个唯一的符号。以下是分配给电话键盘上各按键的频率:
生成一个 DTMF 信号并聆听该信号。
[tones, Fs] = helperDTMFToneGenerator(); p = audioplayer(tones,Fs,16); play(p)
聆听该信号,可分辨出拨了一个三位号码。然而,您无法分辨出拨打的具体号码。接下来,在时域和 650 至 1500 Hz 频带的频域上可视化信号。将 pspectrum 函数的 Leakage 参数设置为 1,以使用矩形窗并提高频率分辨率。
N = numel(tones); t = (0:N-1)/Fs; subplot(2,1,1) plot(1e3*t,tones) xlabel("Time (ms)") ylabel("Amplitude") title("DTMF Signal") subplot(2,1,2) pspectrum(tones,Fs,Leakage=1,FrequencyLimits=[650, 1500])
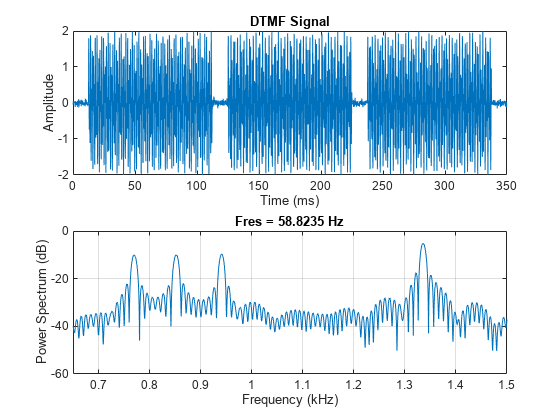
信号的时域图证实存在对应于三个按键的三次能量爆发。为了测量能量爆发的长度,可以取 RMS 包络的脉冲宽度。
env = envelope(tones,80,"rms");
pulsewidth(env,Fs)ans = 3×1
0.1041
0.1042
0.1047
title("Pulse Width of RMS Envelope")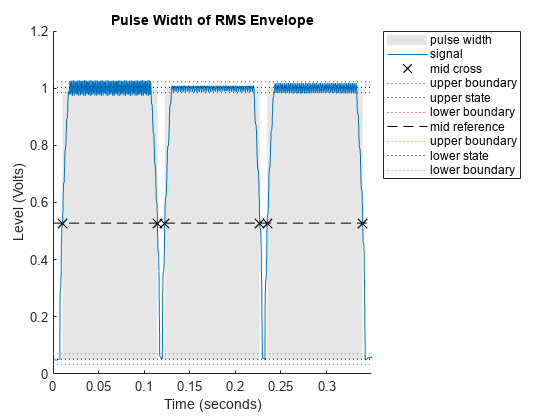
此处您可以看到三个脉冲,每个脉冲长度大约为 100 毫秒。然而,您无法分辨出拨打的是哪个数字。频域图有助于您解决此问题,因为它显示信号中存在的各频率。
通过估计四个不同频带的均值频率来定位频率峰值。
f = [meanfreq(tones,Fs,[700 800]), ... meanfreq(tones,Fs,[800 900]), ... meanfreq(tones,Fs,[900 1000]), ... meanfreq(tones,Fs,[1300 1400])]; round(f)
ans = 1×4
770 852 941 1336
通过将估计的频率与电话键盘的图相匹配,您可以识别出拨打的按键是“5”、“8”和“0”。然而,频域图没有提供任何类型的时间信息来让您知道这些数字的拨打顺序。组合可能是“580”、“508”、“805”、“850”、“085”或“058”。为了解决此难题,请使用 pspectrum 函数计算频谱图,并观察信号的频率成分如何随时间变化。
计算 650 至 1500 Hz 频带的频谱图,并去除低于 10 dB 功率水平的内容,以仅可视化主频率分量。要查看音调持续时间及其在时间上的位置,请使用 0% 重叠。
pspectrum(tones,Fs,"spectrogram",Leakage=1,OverlapPercent=0, ... MinThreshold=-10,FrequencyLimits=[650, 1500]);

频谱图的颜色对频率功率水平进行编码。黄色表示功率较高的频率成分;蓝色表示功率非常低的频率成分。一条亮黄色水平线表示存在某特定频率的音调。该图清楚地显示拨打的所有三个数字中都存在一个 1336 Hz 音调,告诉您它们都在键盘的第二列中。从图中可以看出,先拨打的是最低频率 770 Hz。然后拨打的是最高频率 941 Hz。最后拨打的是中间频率 852 Hz。因此,拨打的号码是 508。
权衡时间和频率分辨率以获得最佳的信号表示
pspectrum 函数将一个信号划分为若干个段。较长的段提供更好的频率分辨率;较短的段提供更好的时间分辨率。可以使用 FrequencyResolution 和 TimeResolution 参数控制段的长度。当未指定频率分辨率或时间分辨率值时,pspectrum 会尝试根据输入信号长度在时间分辨率和频率分辨率之间找到良好的平衡。
假设有以下信号,其采样率为 4 kHz,包含太平洋蓝鲸鲸吟的颤音部分:
load whaleTrill
p = audioplayer(whaleTrill,Fs,16);
play(p)颤音信号由一系列音调脉冲组成。查看在未指定分辨率和时间分辨率设置为 10 毫秒时的时间信号和由 pspectrum 获得的频谱图。将 Leakage 参数设置为 1 以使用矩形窗。由于我们要定位脉冲的时间位置,因此将重叠百分比设置为 0。最后,使用 60 dB 的 MinThreshold 去除频谱图视图中的背景噪声。
t = (0:length(whaleTrill)-1)/Fs; figure ax1 = subplot(3,1,1); plot(t,whaleTrill) ax2 = subplot(3,1,2); pspectrum(whaleTrill,Fs,"spectrogram",OverlapPercent=0, ... Leakage=1,MinThreshold=-60) colorbar(ax2,"off") ax3 = subplot(3,1,3); pspectrum(whaleTrill,Fs,"spectrogram",OverlapPercent=0, ... Leakage=1,MinThreshold=-60,TimeResolution=10e-3) colorbar(ax3,"off") linkaxes([ax1,ax2,ax3],"x")
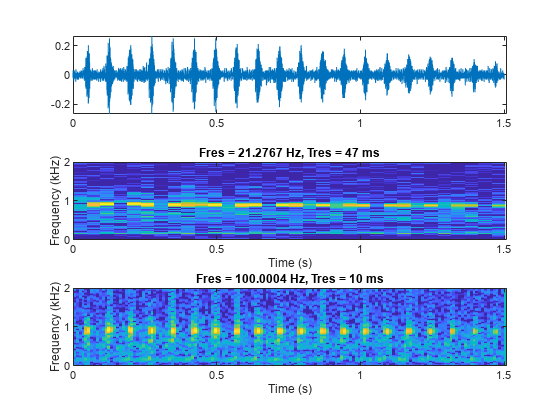
pspectrum 选择的 47 毫秒时间分辨率不够小,不足以定位频谱图中的所有颤音脉冲。另一方面,10 毫秒的时间分辨率足以在时间上定位每个颤音脉冲。如果我们放大几个脉冲,这会变得更加清晰:
xlim([0.3 0.55])
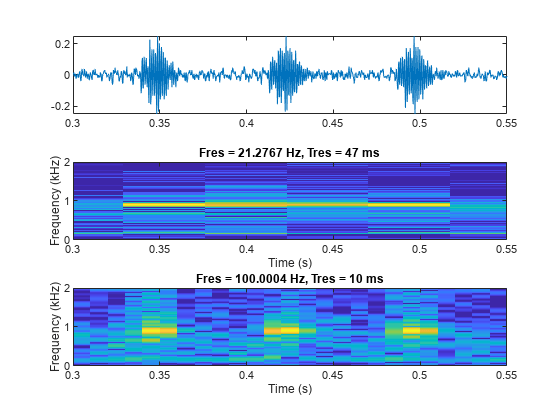
现在加载一个信号,其中包含由一只大棕色蝙蝠(大棕蝠)发出的回声定位脉冲。信号以 7 微秒的采样间隔测量。分析信号的频谱图。
load batsignal Fs = 1/DT; figure pspectrum(batsignal,Fs,"spectrogram")
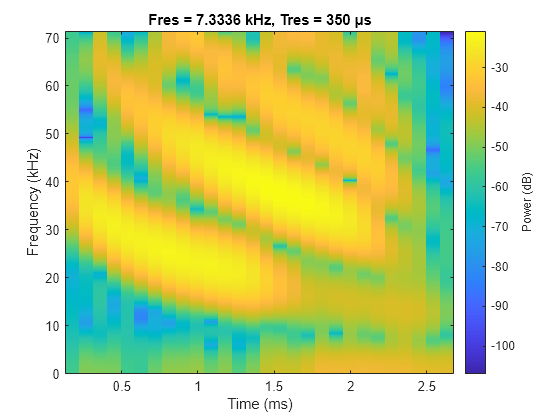
具有默认参数值的频谱图显示四个粗略的时频脊。将频率分辨率值降低到 3 kHz,以获得每个脊的频率变化的更多细节。
pspectrum(batsignal,Fs,"spectrogram",FrequencyResolution=3e3)
注意现在频率脊能够更好地在频率上定位。然而,由于频率分辨率和时间分辨率成反比,频谱图的时间分辨率明显更小。设置 99% 的重叠来对时间窗进行平滑处理。使用 60 dB 的 MinThreshold 来去除不需要的背景内容。
pspectrum(batsignal,Fs,"spectrogram",FrequencyResolution=3e3, ... OverlapPercent=99,MinTHreshold=-60)
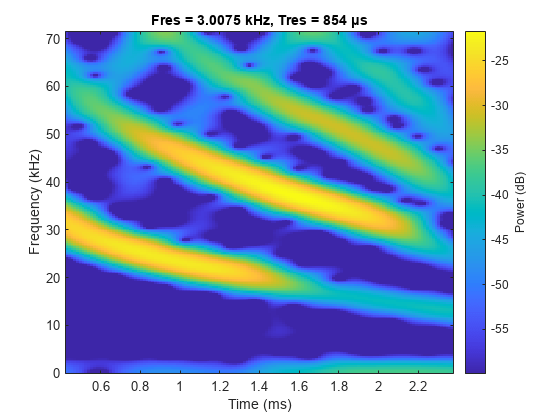
新设置产生的频谱图清晰地显示回声定位信号的四个频率脊。
时频重排
即使我们已能够识别四个频率脊,我们仍可以看到每个脊散布在几个相邻的频率 bin 上。这是由于在时间和频率上使用的加窗方法存在泄漏。
pspectrum 函数能够在时间和频率上估计每个频谱估计值的能量中心。如果您将每个估计值的能量重新赋予最接近新时间和频率中心的 bin,您可以校正该窗的一些泄漏。您可以通过使用 Reassign 参数来完成此操作。将此参数设置为 true 会计算重排后的信号频谱图。
pspectrum(batsignal,Fs,"spectrogram",FrequencyResolution=3e3, ... OverlapPercent=99,MinTHreshold=-60,Reassign=true)
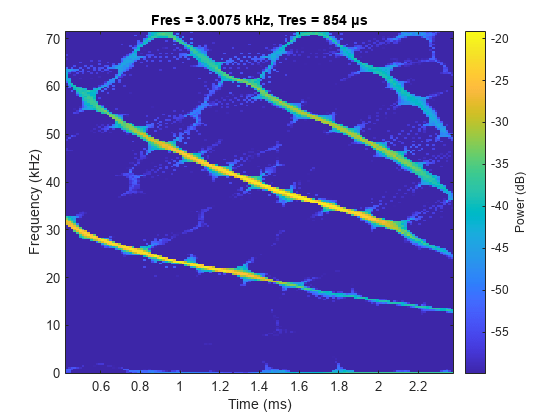
现在频率脊变得更尖锐,在时间上可更好地定位。您也可以使用 fsst 函数来定位信号能量,这将在下一节中讨论。
重新构造时频脊线
假设有以下音频录制,其中包含频率随时间降低的啁啾信号,且最后有一个啪嗒声。
load splat p = audioplayer(y,Fs,16); play(p) pspectrum(y,Fs,"spectrogram")
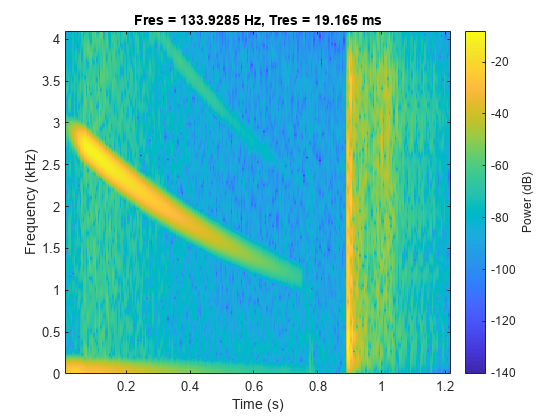
让我们通过在时频平面中提取脊来重新构造“啪嗒”声的一部分。我们使用 fsst 来锐化含噪版本啪嗒信号的频谱,使用 tfridge 来识别啁啾声的脊,并使用 ifsst 来重新构造啁啾。该过程对重新构造的信号进行去噪。
将高斯噪声添加到“啪嗒”声的啁啾部分。添加的噪声对用廉价麦克风录制的音频进行仿真。检查时频频谱内容。
rng("default") t = (0:length(y)-1)/Fs; yNoise = y + 0.1*randn(size(y)); yChirp = yNoise(t<0.35); pspectrum(yChirp,Fs,"spectrogram",MinThreshold=-70)
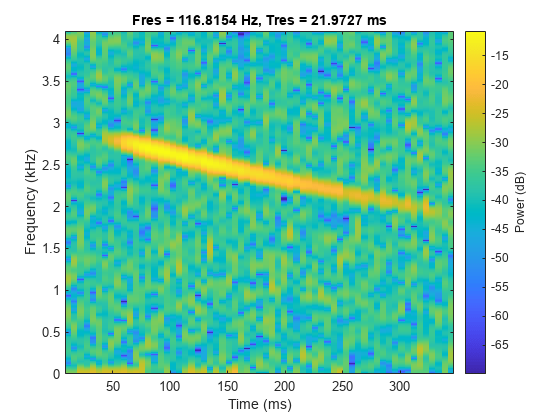
使用傅里叶同步压缩变换 fsst 锐化频谱。fsst 函数通过重新赋予固定时间内频率中的能量,在时频平面中定位能量。计算并绘制噪声啁啾信号的同步压缩变换。
fsst(yChirp,Fs,"yaxis")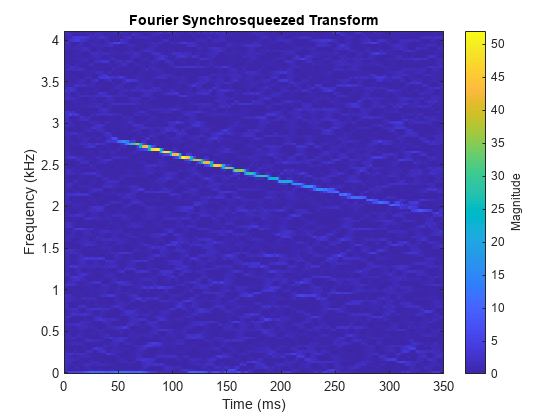
该 chirp 在时频平面中显示为一个局部脊线。使用 tfridge 识别该脊。绘制脊以及变换。
[sst,f] = fsst(yChirp,Fs); [fridge, iridge] = tfridge(sst,f,10); helperPlotRidge(yChirp,Fs,fridge);
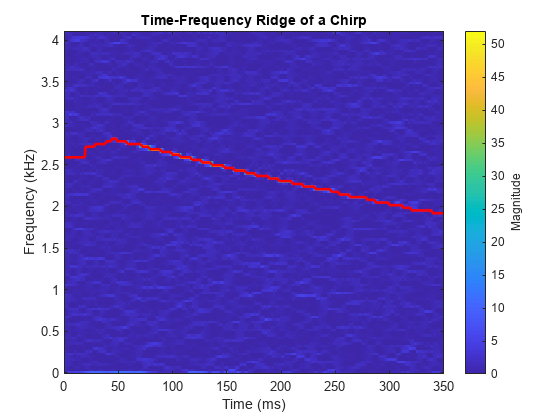
接下来,使用脊索引向量 iridge 重新构造啁啾信号。在脊的两边各包含一个 bin。绘制重新构造的信号的频谱图。
yrec = ifsst(sst,kaiser(256,10),iridge,NumFrequencyBins=1);
pspectrum(yrec,Fs,"spectrogram",MinThreshold=-70)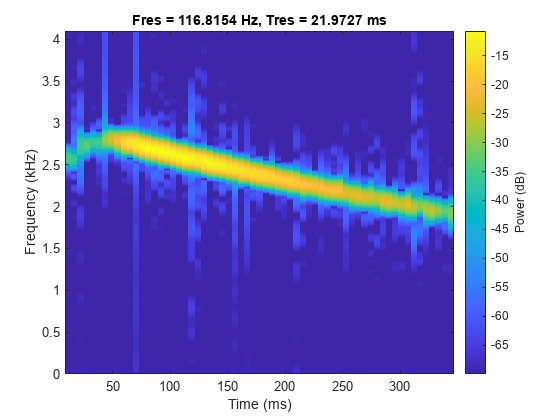
重新构造脊去除了信号中的噪声。连续播放含噪信号和去噪信号,聆听它们的区别。
p = audioplayer([yChirp;zeros(size(yChirp));yrec],Fs,16); play(p);
测量功率
假设有一个复线性调频 (LFM) 脉冲,这是常见的雷达波形。使用 1.27 微秒的时间分辨率和 90% 的重叠来计算信号的频谱图。
Fs = 1e8; bw = 60e6; t = 0:1/Fs:10e-6; IComp = chirp(t,-bw/2,t(end), bw/2,"linear",90)+0.15*randn(size(t)); QComp = chirp(t,-bw/2,t(end), bw/2,"linear",0) +0.15*randn(size(t)); IQData = IComp + 1i*QComp; segmentLength = 128; pspectrum(IQData,Fs,"spectrogram",TimeResolution=1.27e-6,OverlapPercent=90)
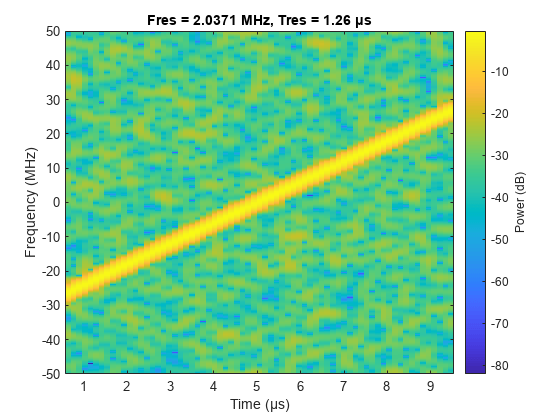
用于计算频谱图的参数给出 LFM 信号的清晰时频表示。pspectrum 计算功率谱图,这意味着颜色值对应于以 dB 为单位的真实功率水平。颜色栏显示信号的功率水平约为 4 dB。
对数频率刻度可视化
在某些应用中,最好将信号的频谱图以对数频率刻度可视化。您可以通过更改 y 轴的 YScale 属性来实现这一点。例如,假设有以 1 kHz 采样的对数啁啾信号。该 chirp 的频率在 10 秒内从 10 Hz 增加到 400 Hz。
Fs = 1e3; t = 0:1/Fs:10; fo = 10; f1 = 400; y = chirp(t,fo,10,f1,"logarithmic"); pspectrum(y,Fs,"spectrogram",FrequencyResolution=1, ... OverlapPercent=90,Leakage=0.85,FrequencyLimits=[1 Fs/2])
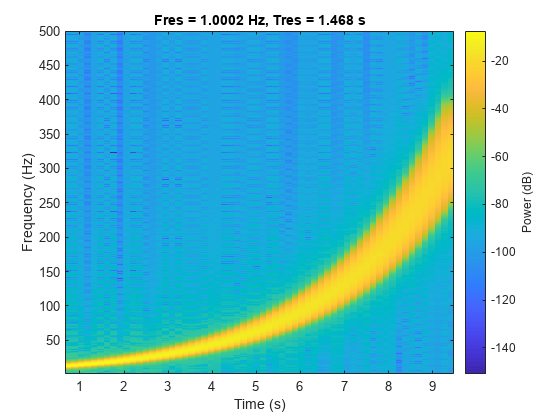
当频率刻度是对数时,chirp 的频谱图变为一条直线。
ax = gca;
ax.YScale = "log";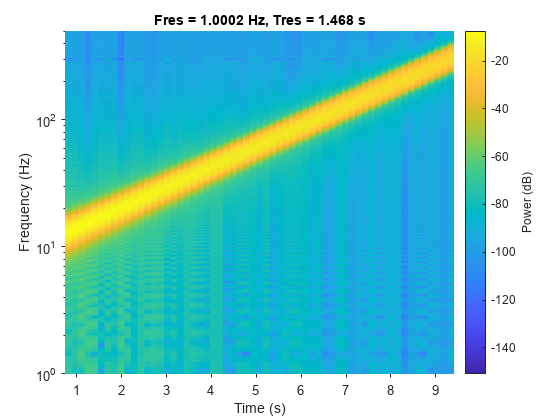
三维瀑布可视化
使用 view 命令,您可以将信号的频谱图可视化为三维瀑布图。您也可以使用 colormap 函数更改显示颜色。
Fs = 10e3;
t = 0:1/Fs:2;
x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*Fs,Fs);
pspectrum(x1,Fs,"spectrogram",Leakage=0.8)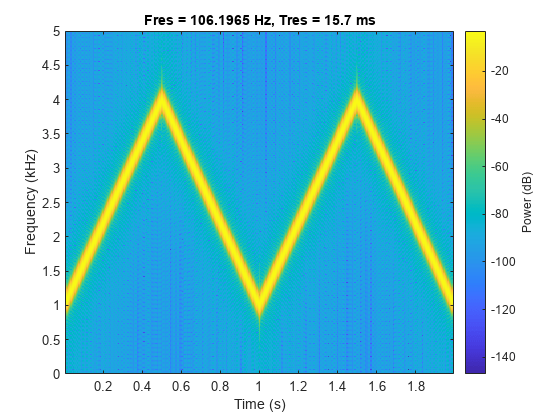
view(-45,65)
colormap bone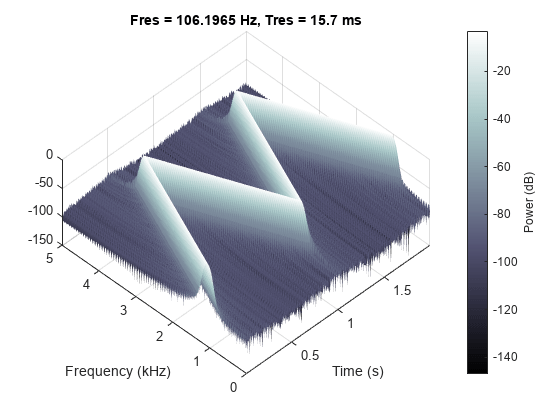
使用持久频谱查找干扰
信号的持久频谱是一个时频视图,显示给定频率在信号中出现的时间所占的百分比。持久频谱是功率-频率空间里的直方图。随着信号演进,特定频率在信号中持续的时间越长,其时间百分比越高,因此其在显示画面中的颜色越亮或“越热”。使用持久频谱来识别隐藏在其他信号中的信号。
假设有一个嵌入在宽带信号中的干扰窄带信号。生成以 1 kHz 进行 500 秒采样的啁啾信号。在测量过程中,chirp 的频率从 180 Hz 增加到 220 Hz。
fs = 1000; t = (0:1/fs:500)'; x = chirp(t,180,t(end),220) + 0.15*randn(size(t));
该信号还包含一个 210 Hz 的干扰,振幅为 0.05,只存在于总信号持续时间的 1/6。
idx = floor(length(x)/6); x(1:idx) = x(1:idx) + 0.05*cos(2*pi*t(1:idx)*210);
计算该信号在 100 至 290 Hz 区间的功率谱。弱正弦波被啁啾信号遮挡。
pspectrum(x,fs,FrequencyLimits=[100 290])
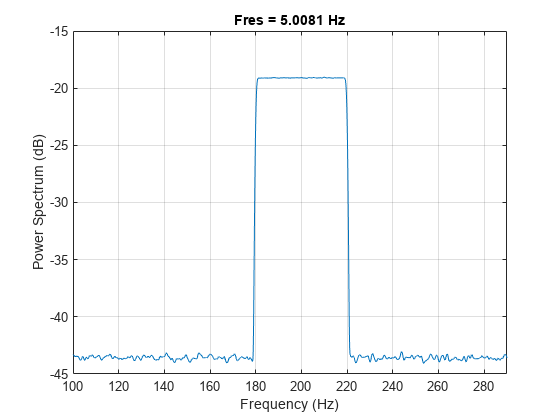
计算该信号的持久频谱。现在两个信号分量都清晰可见。
figure colormap parula pspectrum(x,fs,"persistence",FrequencyLimits=[100 290],TimeResolution=1)
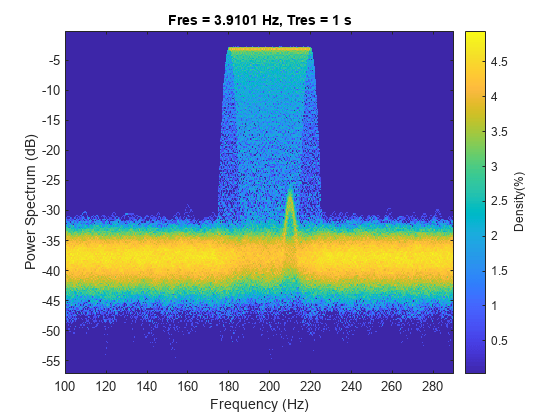
结论
在此示例中,您学习了如何使用 pspectrum 函数执行时频分析,以及如何解释频谱图数据和功率水平。您学习了如何更改时间分辨率和频率分辨率以提高对信号的理解,以及如何使用 fsst、ifsst 和 tfridge 锐化频谱并提取时频脊。您学习了如何配置频谱图以获得对数频率刻度和三维可视化。最后,您学习了如何通过计算持久频谱来找到干扰信号。
附录
此示例中使用以下辅助函数。