对均匀采样信号进行重采样

按有理因子进行速率转换

resample 函数执行从一个采样率到另一个采样率的速率转换。resample 允许您按积分因子 p 进行上采样，然后按另一个积分因子 q 进行抽取。这样，您能够以原始采样率的有理倍数 (p/q) 进行重采样。

要对均匀采样使用 resample 函数，您必须提供此有理因子的分子和分母。要确定所需的整数，可以使用 rat 函数。

以下是从 48 kHz 转换为 44.1 kHz 时如何调用 rat 的示例：

originalFs = 48000;
desiredFs = 44100;

[p,q] = rat(desiredFs / originalFs)

p = 
147

q = 
160

rat 表示可以按 147 进行上采样，按 160 进行下采样。要验证这是否会产生所需的速率，请将 p/q 乘以原始采样率：

originalFs * p / q

ans = 
44100

一旦您确定了新采样率和原始采样率之间的比率，您就可以调用 resample。

例如，使用 48 kHz 的原始采样率创建一段 10 毫秒长的 500 Hz 正弦波，并将其转换为 44.1 kHz：

tEnd = 0.01;
Tx = 0:1/originalFs:tEnd;
f = 500;
x = sin(2*pi*f*Tx);

y = resample(x,p,q);
Ty = (0:numel(y)-1)/desiredFs;

plot(Tx,x,'. ')
hold on
plot(Ty,y,'o ')
hold off
legend('Original','Resampled')

对于上述正弦波等表现良好的信号，仅使用 resample 和精心选择的 p 和 q 就足以正确重新构造信号。

对于具有瞬变或显著噪声的信号，您可能希望对 resample 中的多相抗混叠滤波器有更好的控制。

对瞬变进行滤波

resample 函数在执行速率转换时使用滤波器。这种滤波对信号中的大瞬变很敏感。

为了说明这一点，我们对矩形脉冲进行重采样：

x = [zeros(1,120) ones(1,241) zeros(1,120)];
y = resample(x,p,q);

plot(Tx,x,'-', Ty,y,'-')
legend('Original','Resampled')

该函数很好地重新构造了脉搏的平台区。然而，在脉冲的边沿存在尖峰。

放大第一个脉冲的边沿：

xlim([2e-3 3e-3])

在过渡区域中有阻尼振荡。您可以通过调整内部滤波器的设置来减小这种振荡。

resample 允许您控制应用于抗混叠滤波器的凯塞窗，以减轻某些边沿效果。

两个参数 n 和 beta 控制滤波器的相对长度和它尝试执行的平滑量。n 的较大值表示具有较大的滤波器长度。beta 为 0 表示没有额外的平滑处理。更大的 beta 值表示具有更大的平滑处理。默认情况下，n 为 10，beta 为 5。

一个可行的方法是从默认值开始，并根据需要进行调整。在此处，将 n 设置为 5，将 beta 设置为 20。

n = 5;
beta = 20;

y = resample(x,p,q,n,beta);

plot(Tx,x,'.-')
hold on
plot(Ty,y,'o-')
hold off
legend('Original','Resampled')
xlim([2e-3 3e-3])

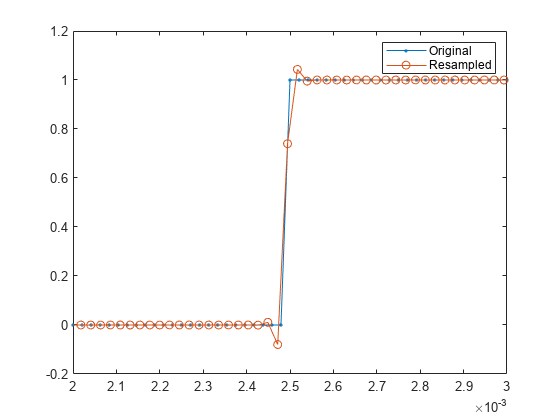
振荡显著减少。

对混叠进行滤波

resample 函数旨在将采样率转换为更高或更低的速率。因此，抗混叠滤波器的截止频率设置为输入或输出采样率的奈奎斯特频率（以较低者为准）。此默认设置使得 resample 函数具有广泛的应用。

有时直接控制滤波器可能是有益的。

为了说明这一点，我们构造并查看一段以 96 kHz 采样的啁啾信号的频谱图。该啁啾信号由一个正弦波组成，其频率在整个奈奎斯特频率范围内从 0 Hz 到 48 kHz 呈二次变化，持续时间为 8 秒：

fs1 = 96000;
t1 = 0:1/fs1:8;
x = chirp(t1, 0, 8, fs1/2, 'quadratic');
spectrogram(x,kaiser(256,15),220,412,fs1,'yaxis')

接下来，使用 resample 的默认设置将啁啾信号转换为 44.1 kHz，并查看频谱图：

fs2 = 44100;

[p,q] = rat(fs2/fs1);
y = resample(x,p,q);

spectrogram(y,kaiser(256,15),220,412,fs2,'yaxis')

在此处，您可以看到原始信号以及不需要的频率成分。理想情况下，正弦波应从 0 Hz 开始，持续到在 5.422 秒时达到 22.05 kHz 的奈奎斯特频率。而实际上，由于在用于重采样的默认滤波器的边缘引入了小的不连续性，从而引入了伪影。为了防止这些伪影，您可以提供较长的滤波器，其截止频率略低，阻带抑制比默认滤波器更大。

为了获得适当的时序对齐，滤波器应具有奇数长度。长度应比 p 或 q 大几倍（以较大者为准）。同样，将所需的归一化截止频率除以 p 或 q 中的较大值。在任一情况下，都将生成的系数乘以 p。

下面是一个滤波器示例，其截止频率为输出奈奎斯特频率的 98% (0.98)，阶数为 256 乘以抽取因子，采用凯塞窗进行加窗且 beta 为 12。

normFc = .98 / max(p,q);
order = 256 * max(p,q);
beta = 12;

lpFilt = firls(order, [0 normFc normFc 1],[1 1 0 0]);
lpFilt = lpFilt .* kaiser(order+1,beta)';
lpFilt = lpFilt / sum(lpFilt);

% multiply by p
lpFilt = p * lpFilt;

% resample and plot the response
y = resample(x,p,q,lpFilt);
spectrogram(y,kaiser(256,15),220,412,fs2,'yaxis')

请注意，混叠已去除。

延伸阅读

有关重采样的详细信息，请参阅 Signal Processing Toolbox。

Reference: fredric j harris, "Multirate Signal Processing for Communications Systems", Prentice Hall, 2004.