本页采用了机器翻译。点击此处可查看最新英文版本。

通过测量协议和数据分析对熵系数进行参数化

自 R2024a 起
打开实时脚本

本例展示了如何进行试验以及如何分析试验数据，以参数化熵系数。熵热是电池热模型中的可逆热生成项。该方程用于计算熵热。

Q˙rev=I* T*dUdT,

其中，I 表示电池电流，T 表示电池温度，dU/dT 表示熵热系数。熵热系数主要取决于荷电状态 (SOC)。Battery Equivalent Circuit 模块通过指定可逆热模型和熵系数参数，提供建模可逆熵热的能力。

要测量电池电芯的熵热系数，必须扫描不同的 SOC 水平，并逐个 SOC 表征熵热系数。要达到不同的 SOC 水平，首先需要向电池施加脉冲放电电流。然后让电芯静置，直到达到电化学平衡。为了缩短达到电化学平衡所需的休息时间，将 SOC 扫描放电和休息过程在相对较高的环境箱温度（如 30°C）下进行。

这些图展示了用于表征熵热系数的测试方法。左图显示了测得的电池端电压。右侧的图显示了测得的输入电流。

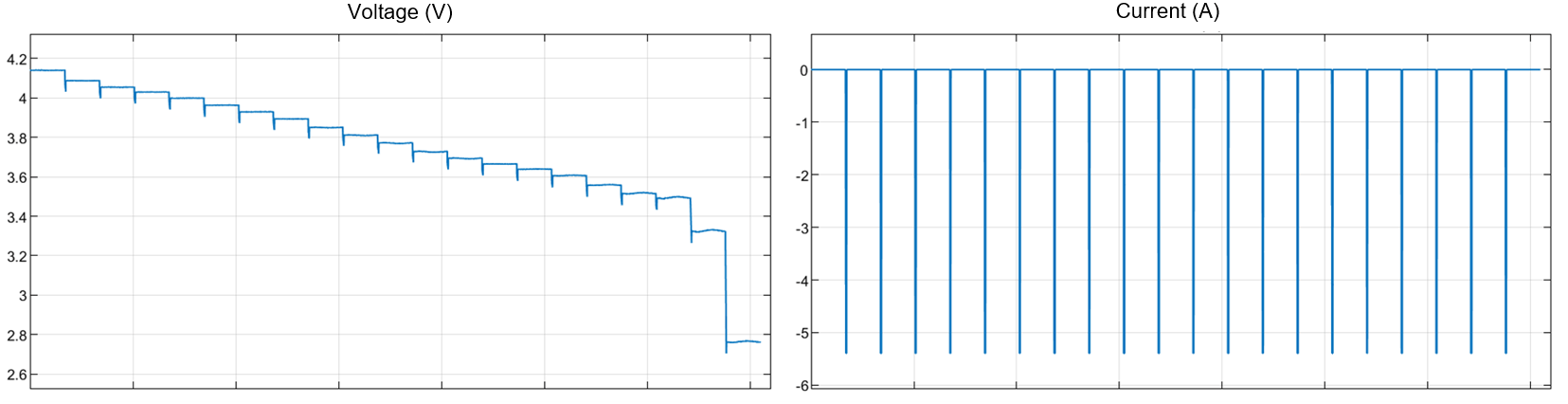
在每个 SOC，您对电芯进行热循环，并在电芯温度接近环境箱的设定点温度后，测量每个温度下的开路电压 (OCV)。在这些图中，环境试验箱的温度设定值依次循环为 30、40、30、20、10、5、10、20 和 30 摄氏度。

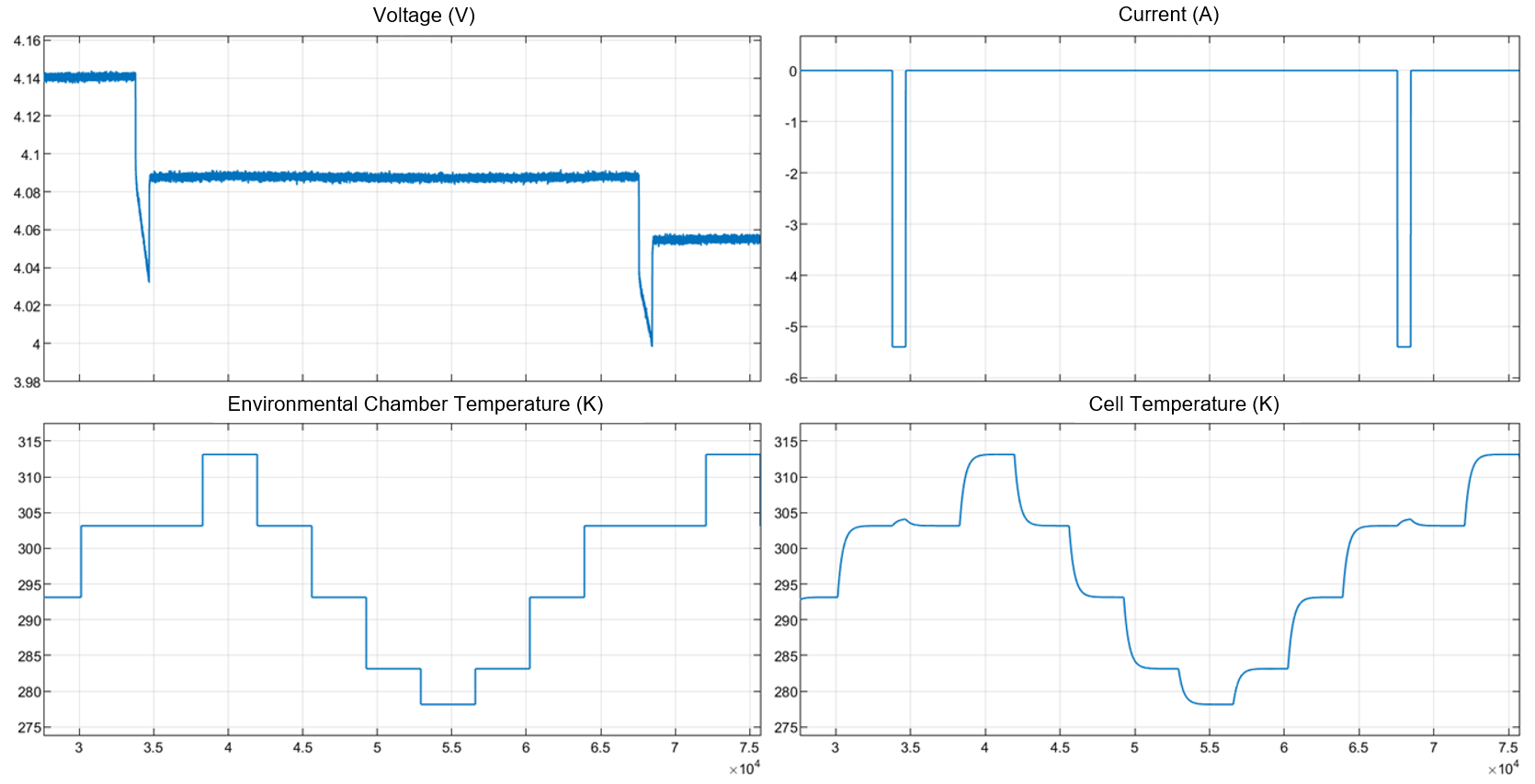
为了尽量减少电池测试仪电压测量噪声对 SOC 计算的影响，并计算 SOC 的熵热系数，您需要对 OCV 在一定温度设定点范围内进行线性拟合。这是因为熵热系数通常在 0.1 mV/K 量级，而电池测试仪的测量精度通常为 1 mV。

生成合成数据

在实际应用中，您可以用试验室中的真实试验代替 Simscape 模型仿真。此示例中的 Simscape 模型详细描述了 SOC 和温度扫描的测试程序。然后，您可以将这些详细信息复制到实际的试验设置中。

打开 ModelForSimulatingTest 模型。

open_system("ModelForSimulatingTest.slx")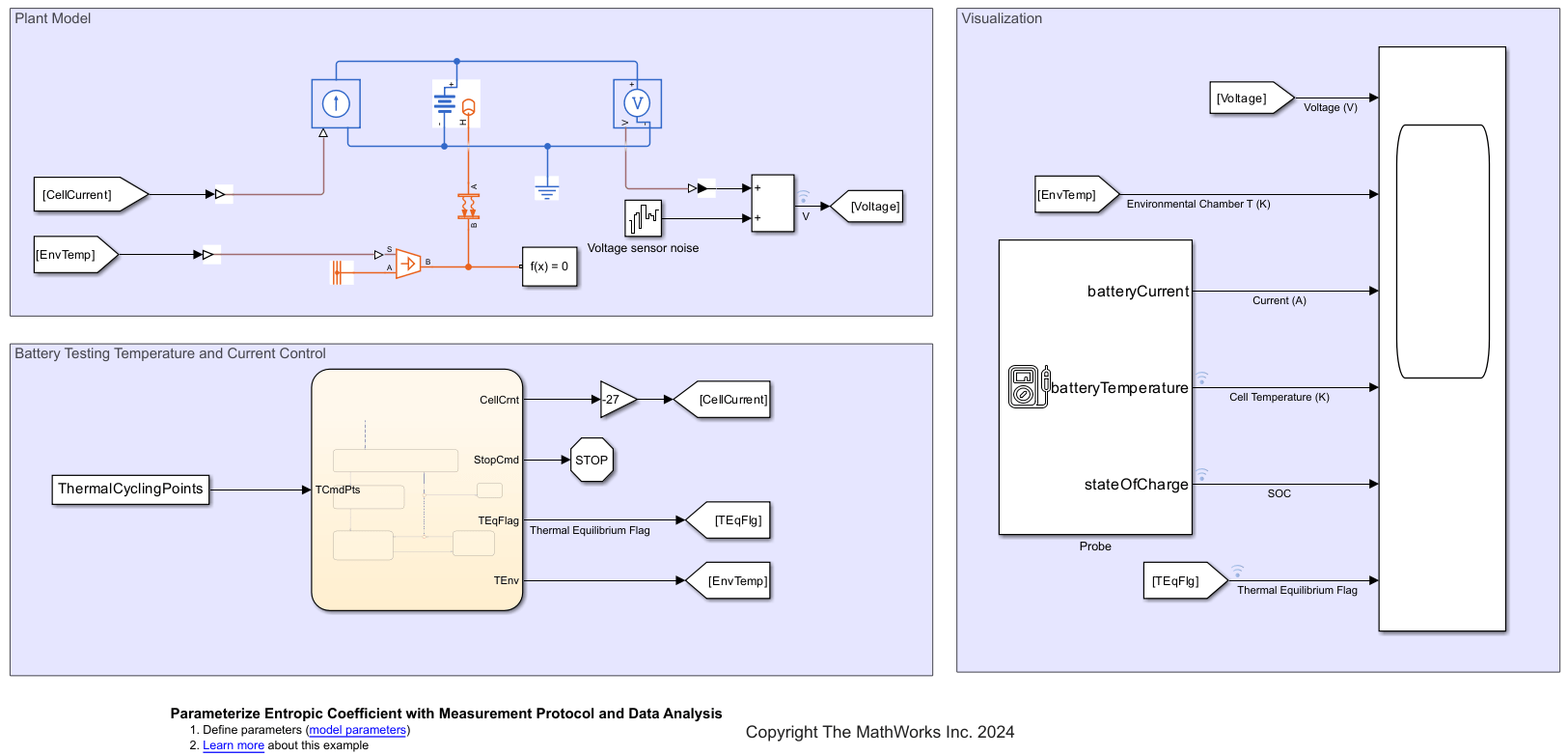

此示例已为 Battery Equivalent Circuit 模块的 OCV 提供了适当的参数化值，以准确反映 OCV 随温度的变化。为了模拟真实试验中的电压测量噪声，该模型在仿真电压中添加了带限白噪声。此噪声的标准差设置为 1mV。

对模型进行仿真。

out=sim("ModelForSimulatingTest.slx");

从仿真数据中提取时间、电压、SOC、温度和热平衡标志。

t = out.logsout{1}.Values.Time;
voltage = out.logsout{1}.Values.Data;
temperatureFlag = out.logsout{2}.Values.Data;
soc = out.logsout{4}.Values.Data;
T = out.logsout{3}.Values.Data;

分析数据以计算熵热系数

使用来自 Simscape 模型中的合成数据，通过将 OCV 数据与热循环期间的温度进行拟合，对每个 SOC 进行分析。

为了展示 OCV 数据的噪声以及拟合的 OCV 与温度曲线的偏差，本代码绘制了在 SOC 水平为 0、0.5 和 1 时，OCV 随温度的变化曲线。如果您有实际试验结果，可以使用这些结果替换合成数据。

dUdTExp = zeros(size(SOC_vec2));
figure(Position=[0 0 2000 600]);
tiledlayout(1,3)
for i = 1:numel(SOC_vec2)
    indx = find(abs(soc-SOC_vec2(i))<1.5e-3 & temperatureFlag == 1);
    dUdTfit = polyfit(T(indx), voltage(indx),1);
    T_x = linspace(min(T(indx)), max(T(indx)),100);
    dUdT_y = polyval(dUdTfit, T_x);
    if mod(i,10) == 1
        nexttile
        plot(T(indx), voltage(indx),'o', T_x, dUdT_y);
        xlabel('temperature (K)');
        ylabel('OCV (V)');
        title(sprintf('%.2f SOC',SOC_vec2(i)));
    end

    dUdTExp(1,i) = dUdTfit(1)*1000; % converting V/K to mV/K 
  
end

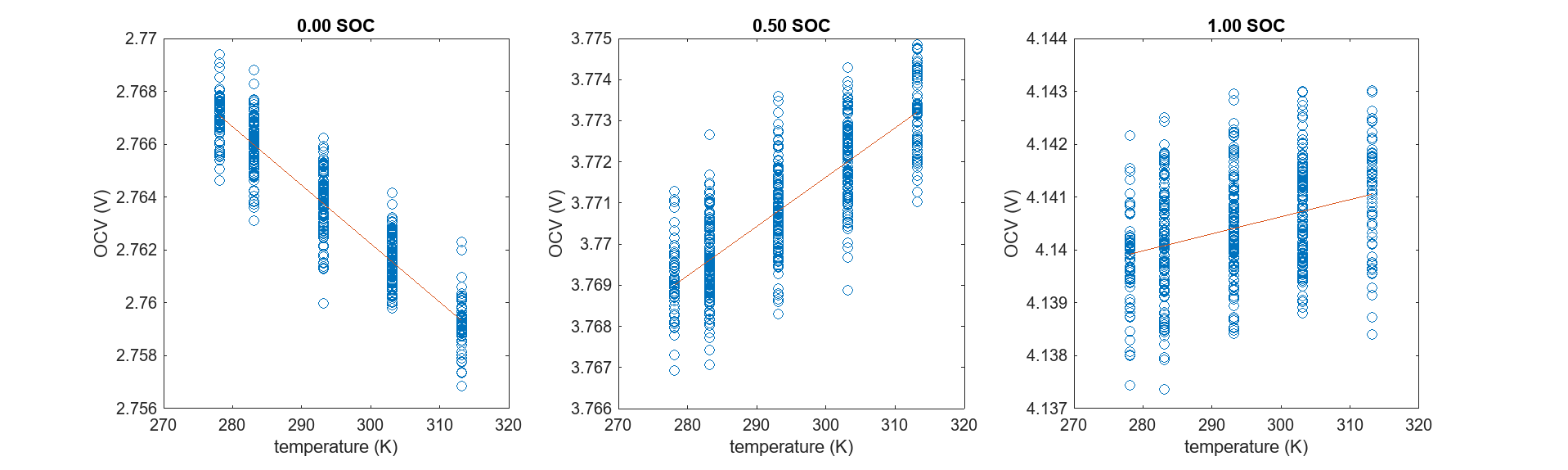
Figure contains 3 axes objects. Axes object 1 with title 0.00 SOC, xlabel temperature (K), ylabel OCV (V) contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 2 with title 0.50 SOC, xlabel temperature (K), ylabel OCV (V) contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 3 with title 1.00 SOC, xlabel temperature (K), ylabel OCV (V) contains 2 objects of type line. One or more of the lines displays its values using only markers

请注意，电压数据存在噪声，这在实际试验数据中也是常见的情况。然而，通过线性拟合获得拟合直线的斜率可以解决数据噪声问题。拟合直线的斜率，即 OCV 与温度的关系，可以是正的或负的。这是可以预期的，因为熵热系数可以是正值或负值。熵热系数的符号取决于电化学性质、化学计量比和自放电状态 (SOC)。

然后，在 Simscape 模型中的 Battery Equivalent Circuit 模块中，使用熵热系数为不同温度下的每个 SOC 正确参数化 OCV。

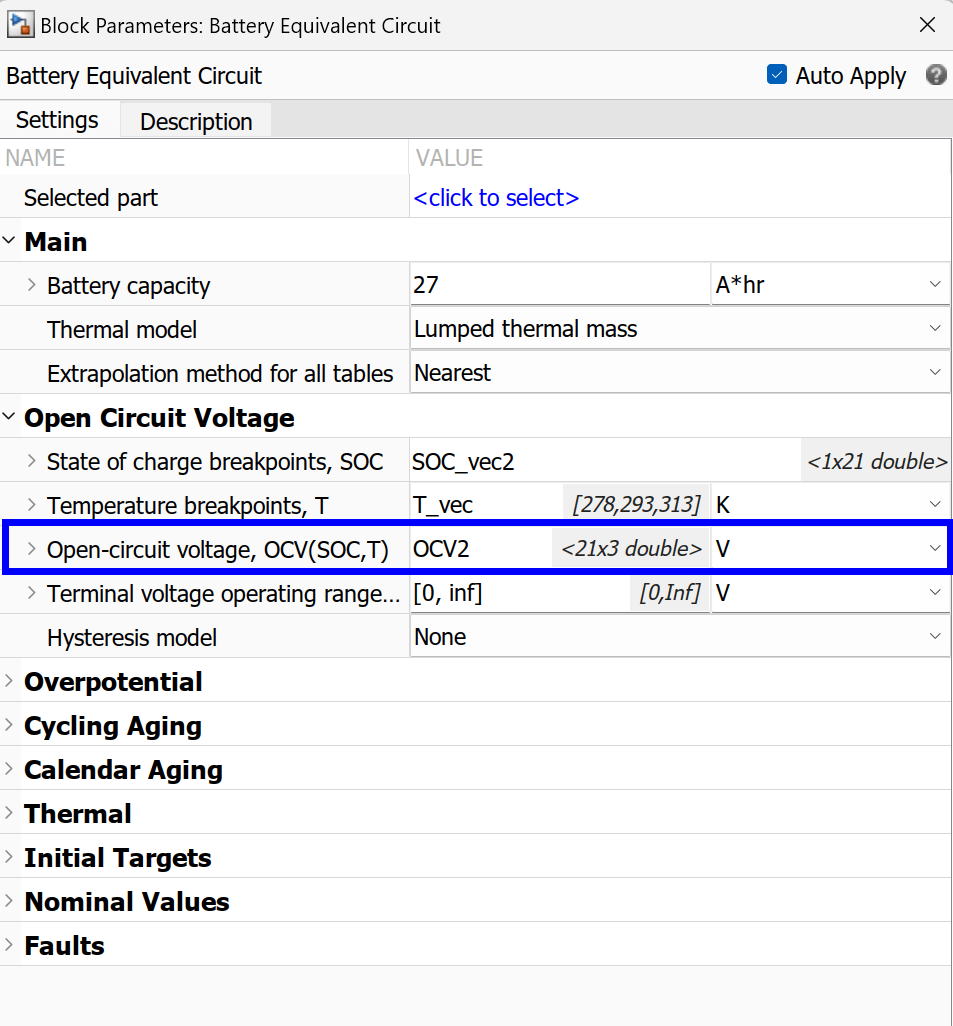
将测量得到的熵热系数与基准值进行比较

将结果与用于生成合成数据的 Simscape 模型中使用的基准数据进行比较 [1]。 

figure; plot(SOC_vec2, dUdTExp,'x', SOC_vec2,dUdT2, 's');
legend({'measured', 'benchmark'});
xlabel('SOC (-)');
ylabel('Entropic coefficient dU/dT (mV/K)')

测得的熵热系数与基准值非常吻合。测量程序和数据分析方法在处理电压测量噪声问题时效果良好，这得益于熵热系数非常低的特性。

在热模型中的 Battery Equivalent Circuit 模块中实现熵热系数

从试验测量中加载参数化熵热系数变量。

if ~exist('dUdTExp','var')
    load dUdTExp.mat;
end

打开模型。

open_system('ThermalModelWithEntropicHeat.slx');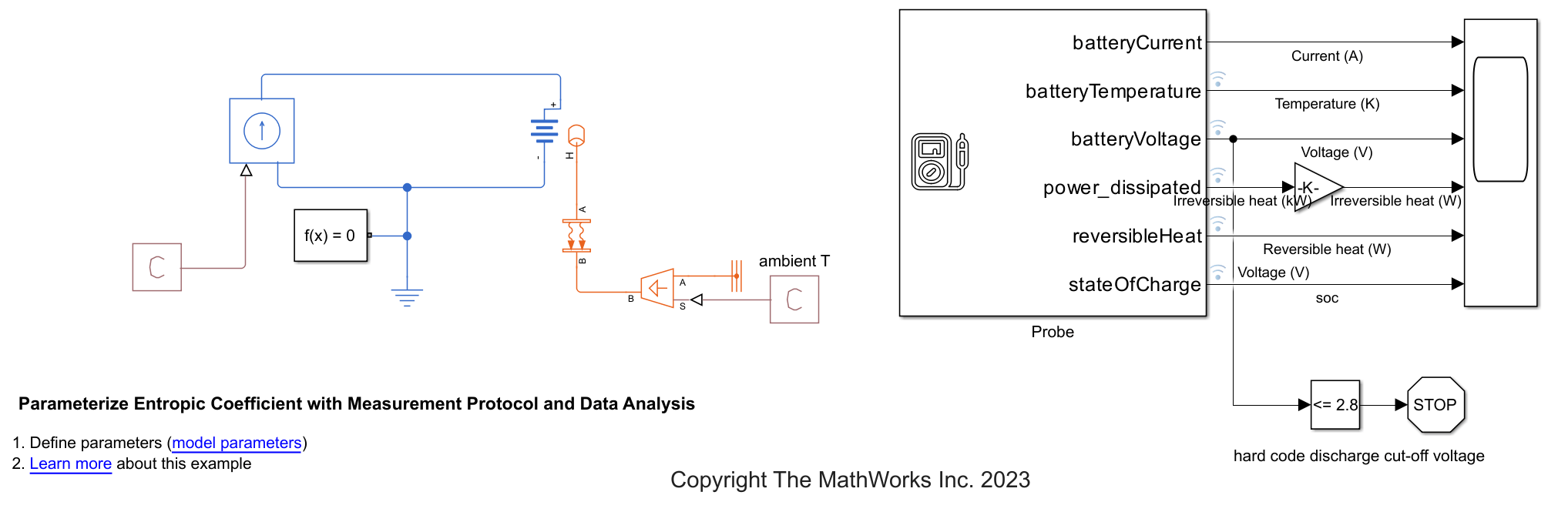

启用 Battery Equivalent Circuit 模块的可逆热模型。将可逆热模型参数设置为 EntropicCoefficient。

set_param('ThermalModelWithEntropicHeat/Battery Equivalent Circuit','ReversibleHeatModel','2');

将熵系数参数设置为 "dUdTExp"。

set_param('ThermalModelWithEntropicHeat/Battery Equivalent Circuit', 'EntropicCoefficient', 'dUdTExp');
C_rate = [0.1 0.5 1 2];
figure(Position=[0 0 1600 400]);
tiledlayout(1,4)

for j = 1:numel(C_rate)
    
    set_param('ThermalModelWithEntropicHeat/PS Constant', 'constant', num2str(-C_rate(j)*27));
    set_param('ThermalModelWithEntropicHeat/Convective Heat Transfer', 'heat_tr_coeff', num2str(C_rate(j)^2*200));
    set_param('ThermalModelWithEntropicHeat','StopTime',num2str(3600/C_rate(j)));
    out = sim("ThermalModelwithEntropicHeat.slx");
    Q_entrop_ts = out.logsout{2}.Values;
    Q_resist_ts = out.logsout{1}.Values;
    TM_SOC_ts = out.logsout{5}.Values;


    nexttile
    plot(TM_SOC_ts.Data,Q_entrop_ts.Data,'--',TM_SOC_ts.Data,Q_resist_ts.Data*1000); 
    
    title(sprintf('Discharge rate %2.1f C', C_rate(j)))
    lgd=legend({'reversible heat','irreversible heat'}, Location="southwest");
    xlabel('SOC');
    ylabel('Heat generation rate (W)');
    ax = gca; ax.XDir = "reverse";
end
lgd.Layout.Tile = 'east';

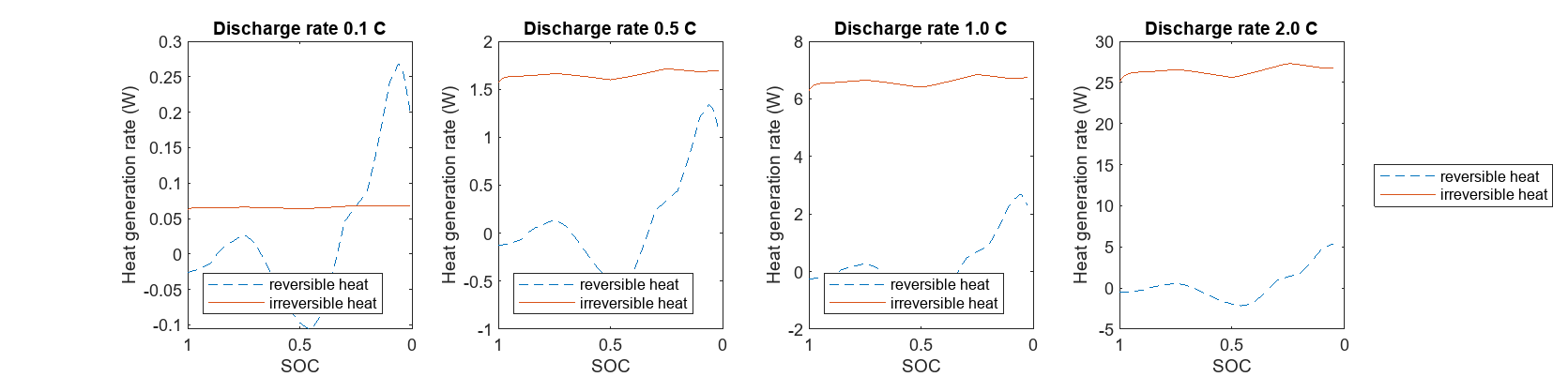
Figure contains 4 axes objects. Axes object 1 with title Discharge rate 0.1 C, xlabel SOC, ylabel Heat generation rate (W) contains 2 objects of type line. These objects represent reversible heat, irreversible heat. Axes object 2 with title Discharge rate 0.5 C, xlabel SOC, ylabel Heat generation rate (W) contains 2 objects of type line. These objects represent reversible heat, irreversible heat. Axes object 3 with title Discharge rate 1.0 C, xlabel SOC, ylabel Heat generation rate (W) contains 2 objects of type line. These objects represent reversible heat, irreversible heat. Axes object 4 with title Discharge rate 2.0 C, xlabel SOC, ylabel Heat generation rate (W) contains 2 objects of type line. These objects represent reversible heat, irreversible heat.

对于本例中的特定参数组合，可逆热量与不可逆热量在低速应用中相当，例如 1C 或更低的速率。然而，随着 C 值的增高，可逆热量开始变得微不足道，与不可逆热量相比，这符合预期，因为不可逆热量的大部分来自电阻热。电阻热与电流的平方成正比，这是基于焦耳定律和欧姆定律。熵热与电流成正比。

参考资料

[1] Geng, Zeyang, et al.‘A Time- and Cost-Effective Method for Entropic Coefficient Determination of a Large Commercial Battery Cell’.IEEE Transactions on Transportation Electrification, vol. 6, no. 1, Mar. 2020, pp. 257–66.DOI.org (Crossref), https://doi.org/10.1109/TTE.2020.2971454.

另请参阅

主题