Main Content

Translational Hard Stop (PB)

Hard stop in position-based mechanical translational systems

Since R2024b

expand all in page
  • Translational Hard Stop (PB) block

Libraries:
Simscape / Foundation Library / Translational / Elements

Description

The Translational Hard Stop (PB) block represents a mechanical translational hard stop that restricts the relative position of two bodies to be greater than or equal to 0 m. You can model contact between the two bodies either as a continuous spring and damper or as an instantaneous impulse based on a coefficient of restitution.

Connections B and F are position-based mechanical translational conserving ports. When the hard stop is disengaged, port F has a more positive position than port B. Force acts from port B on port F. Positive force acts to disengage the hard stop. Length is the gap between the two sides of the hard stop:

length=xF−xB

where xB and xF are absolute positions of ports B and F, respectively.

Models Based on Stiffness and Damping

In hard stop models based on stiffness and damping, the impact interaction between the two sides is assumed to be elastic. The block models this elasticity with the Contact stiffness parameter. To account for energy dissipation and nonelastic effects, the block uses the Contact damping parameter.

The basic hard stop model, Full stiffness and damping applied at bounds, damped rebound, uses these equations:

f={−K⋅length−D⋅vfor length≤00for length>0

v=vF−vB

where:

  • f is the interaction force between the two sides.

  • K is the contact stiffness.

  • D is the damping coefficient.

  • v is the relative velocity.

  • vF and vB are the absolute velocities of ports B and F, respectively.

In the Full stiffness and damping applied at bounds, undamped rebound hard stop model, the equations contain an additional term, ge(v,0). This term ensures that the block does not apply damping on the rebound.

f={−K⋅length−D⋅v⋅ge(v,0)for length≤00for length>0

The relational function ge (greater than or equal) does not generate zero crossings when the velocity changes sign. For more information, see Enabling and Disabling Zero-Crossing Conditions in Simscape Language. However, the solver treats the ge function as nonlinear. Therefore, if simscape.findNonlinearBlocks indicates that the rest of your network is linear or switched linear, use the Full stiffness and damping applied at bounds, damped rebound model to improve performance.

The default hard stop model, Stiffness and damping applied smoothly through transition region, damped rebound, adds a transition region to the equation. In the transition region, the block smoothly ramps up the force from zero to the full value. At the end of the transition region, the block applies the full stiffness and damping. On the rebound, the block smoothly decreases both stiffness and damping forces to zero. These equations also use the ge relational function, which does not produce zero crossings.

Model Based on Coefficient of Restitution

Unlike the models based on stiffness and damping, this model does not allow penetration of the two sides of the hard stop. The hard stop behavior is represented by a mode chart with two regular modes and two instantaneous modes:

  • FREE — There is no force transmission between the two sides of the hard stop. In this mode, f = 0, length >= 0.

  • CONTACT — The gap is closed. In this mode, v = 0, length < 0.

  • RELEASE — The instantaneous mode needed to transition from CONTACT to FREE.

  • IMPACT — The instantaneous mode used when the two sides of the hard stop bounce.

When the two sides of the hard stop hit each other slowly, with a relative speed less than the static contact speed threshold, the two sides stay in contact. Otherwise, the sides bounce. When the sides bounce, they lose speed due to the coefficient of restitution. In contact mode, the relative speed is 0. To transition from the contact mode to free mode, a tensile force greater than the static contact release force threshold must be applied to the hard stop, and the transition must go through an instantaneous release mode to set the initial speed.

This modeling option improves simulation performance because static contact mode does not require the block to keep computing hard stop force when the block is in contact mode.

Variables

To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.

Examples

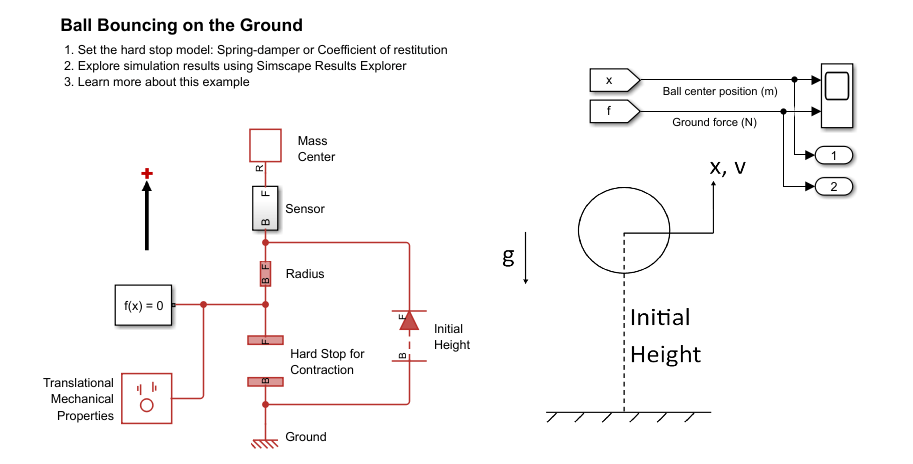
Hard Stops in the Position-Based Translational Domain

Hard Stops in the Position-Based Translational Domain

Configure Translational Hard Stop (PB) blocks in several simple position-based mechanical translational models and interpret the model behavior. This example describes how to model systems with upper and lower bounds, choose a hard stop model parameterization, set initial targets for variables, and interpret the logged forces.

Ports

Conserving

expand all

Position-based mechanical translational conserving port that represents the base connection.

Position-based mechanical translational conserving port that represents the follower connection. When the hard stop is disengaged, port F has a more positive position than port B.

Parameters

expand all

Select the hard stop model:

  • Stiffness and damping applied smoothly through transition region, damped rebound — Specify a transition region, in which the force ramps up from zero. At the end of the transition region, the block applies the full stiffness and damping. This model applies damping on the rebound, but damping is limited to the value of the stiffness force. Therefore, damping can reduce or eliminate the force provided by the stiffness, but never exceed it. All equations are smooth and produce no zero crossings.

  • Full stiffness and damping applied at bounds, undamped rebound — This model has full stiffness and damping applied with impact, with no damping on the rebound. The equations produce no zero crossings when velocity changes sign, but there are position-based zero crossings. This model has nonlinear equations.

  • Full stiffness and damping applied at bounds, damped rebound — This model has full stiffness and damping applied with impact, with damping applied on the rebound as well. The equations are switched linear, but produce position-based zero crossings. Use this hard stop model if simscape.findNonlinearBlocks indicates that this block prevents the whole network from being switched linear.

  • Based on coefficient of restitution — This model uses a mode chart with regular and instantaneous modes to represent the hard stop behavior. All equations are smooth and produce no zero crossings. This modeling option improves simulation performance.

Elastic property of the colliding bodies. The greater the value of this parameter, the less the bodies penetrate into each other and the more rigid the impact becomes. Setting this parameter to lesser values makes contact softer, but generally improves convergence and computational efficiency.

Dependencies

To enable this parameter, set Hard stop model to

  • Stiffness and damping applied smoothly through transition region, damped rebound

  • Full stiffness and damping applied at bounds, undamped rebound

  • Full stiffness and damping applied at bounds, damped rebound

Dissipating property of the colliding bodies. The greater the value of this parameter, the more energy dissipates during impact.

Dependencies

To enable this parameter, set Hard stop model to

  • Stiffness and damping applied smoothly through transition region, damped rebound

  • Full stiffness and damping applied at bounds, undamped rebound

  • Full stiffness and damping applied at bounds, damped rebound

Region where the force ramps up from zero to the full value. At the end of the transition region, the block applies full stiffness and damping.

Dependencies

To enable this parameter, set Hard stop model to Stiffness and damping applied smoothly through transition region, damped rebound.

Ratio of the final to the initial relative speed between the two bodies after the collision.

Dependencies

To enable this parameter, set Hard stop model to Based on coefficient of restitution.

Select the hard stop initial state:

  • Free — There is no force transmission between the sides of the hard stop. Initialize the hard stop by specifying relative velocity and gap length.

  • In contact — The gap between the sides of the hard stop is closed. Initialize the hard stop by specifying force.

Dependencies

To enable this parameter, set Hard stop model to Based on coefficient of restitution.

Threshold relative speed between the two bodies before the collision. When the two bodies collide with speed less than the value of this parameter, they stay in contact. To avoid modeling static contact between the two bodies, set this parameter to 0.

Dependencies

To enable this parameter, set Hard stop model to Based on coefficient of restitution.

Minimum force needed to release the two bodies from a static contact mode.

Dependencies

To enable this parameter, set Hard stop model to Based on coefficient of restitution.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2024b

See Also

| |

Topics