Main Content

Increase Simulation Speed Using the Partitioning Solver

The Partitioning solver is a Simscape™ fixed-step local solver that improves performance for certain models by reducing computational cost of simulation. Decreased computational cost yields faster simulation rates for desktop simulation and decreased task execution time (TET) for deployment. The solver converts the entire system of equations for the attached Simscape network into several smaller sets of switched linear equations that are connected through nonlinear functions. Computational cost is reduced because it is more efficient to calculate solutions for several smaller equation systems than it is to calculate the solution for one large system of equations.

The Partitioning solver does not partition models, that is it does not split a model into separate subsystems for multicore processing. To learn how to partition a Simscape model, see Partition a Model.

To use the Partitioning solver, open the Solver Configuration block settings and:

  1. Select the Use local solver check box.

  2. Set the Solver type parameter to Partitioning.

  3. Clear the Start simulation from steady state check box.

  4. Set the Equation formulation parameter to Time.

For real-time simulation, also select the Use fixed-cost runtime consistency iterations check box. For more information, see Make Your Model Real-Time Viable.

Limitations

Not all networks can simulate with the Partitioning solver. A simulation that uses the Partitioning solver results in an error if the Simscape network cannot be represented by switched linear equations connected through nonlinear functions. Simulating with the Partitioning solver also yields an error for networks that contain:

Certain Solver Configuration block settings are not compatible with the Partitioning solver. A simulation that uses a Partitioning solver results in an error if the model contains a Solver Configuration block with:

  • Start simulation from steady state selected

  • Equation formulation set to Frequency and time

Options

To further improve simulation performance, you can set the Partition storage method parameter to Exhaustive and specify a value for the Partition memory budget [kB] parameter, based on the Total memory estimate data in the Statistics Viewer. For more information, see Solver Configuration and Partitioning Solver Statistics.

Simulate a Simscape Model Using the Partitioning Solver

Open Model

This example shows how to compare the speed and the accuracy of a simulation that uses the Partitioning solver to baseline results. It also shows how to compare the speeds of the Partitioning solver and the Backward Euler solver.

To open the DC motor model as a workspace variable, enter:

open_system("PermanentMagnetDCMotor")
model = 'PermanentMagnetDCMotor';

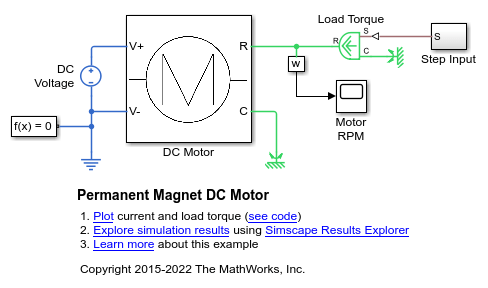
To return all simulation outputs within a single Simulink.SimulationOutput object so that you can later compare simulation times, enable the single-output format of the sim command.

% Enable single-output format
set_param(model,'ReturnWorkspaceOutputs', 'on')

Enable the signal that goes to the Motor RPM scope block for Simulink® data logging and viewing with the Simulink&reg Data Inspector.

% Define the w sensor subsystem and the path
%    to it as variables
rpmSensor = 'Sensing';
rpmSensorPath = [model,'/',rpmSensor];

% Mark the output signal from the w sensor subsystem
%   for Simulink(R) data logging
phRpmSensor = get_param(rpmSensorPath,'PortHandles');
set_param(phRpmSensor.Outport(1),'DataLogging','on')

The logging badge marks the signal in the model.

Run timed simulations for each of these solvers:

  • Variable-step global solver, the original solver for the model

  • Fixed-step local Backward Euler solver

  • Fixed-step local Partitioning solver

% Define the Solver Configuration block and the path
%    to it as variables
solvConfig = 'Solver Configuration';
solvConfigPath = [model,'/',solvConfig];

% Run a timed simulation using the original solver
out = sim(model);
tBaseline = out.SimulationMetadata.TimingInfo.ExecutionElapsedWallTime;

% Select option Solver Configuration >  Use local solver
set_param(solvConfigPath, 'UseLocalSolver', 'on')

% Set Solver Configuration >  Solver type > Partitioning
set_param(solvConfigPath, 'LocalSolverChoice',...
    'NE_PARTITIONING_ADVANCER')

% Run a timed simulation using the Partitioning solver
out = sim(model);
tPartition = out.SimulationMetadata.TimingInfo.ExecutionElapsedWallTime;

% Set Solver Configuration >  Solver type > Backward Euler
set_param(solvConfigPath, 'UseLocalSolver', 'on',...
    'LocalSolverChoice','NE_BACKWARD_EULER_ADVANCER')

% Run a timed simulation using the Backward Euler solver
out = sim(model);
tBackEuler = out.SimulationMetadata.TimingInfo.ExecutionElapsedWallTime;

% Compute the percent difference for the simulation times
spdPartitionVsBaseline = 100*(tBaseline - tPartition)/tBaseline;
spdBackEulerVsBaseline = 100*(tBaseline - tBackEuler)/tBaseline;
spdPartitionVsBackEuler = 100*(tBackEuler - tPartition)/tBackEuler;

% Reset the solver to the original setting by deselecting Use local solver
set_param(solvConfigPath, 'UseLocalSolver', 'off')

compTimeDiffTable = table({'Baseline';...
    'Partitioning';...
    'Backward Euler'},...
    {tBaseline;tPartition;tBackEuler},...
'VariableNames', {'Solver','Sim_Duration'});

display(compTimeDiffTable);

compTimeDiffTable =

  3x2 table

          Solver          Sim_Duration
    __________________    ____________

    {'Baseline'      }     {[0.0382]} 
    {'Partitioning'  }     {[0.0057]} 
    {'Backward Euler'}     {[0.0122]} 


compPctDiffTable = table({'Partitioning versus Baseline';...
    'Backward Euler versus Baseline';...
    'Partitioning versus Backward Euler'},...
    {spdPartitionVsBaseline;...
    spdBackEulerVsBaseline;...
    spdPartitionVsBackEuler},...
'VariableNames', {'Comparison','Percent_Difference'});

display(compPctDiffTable);

compPctDiffTable =

  3x2 table

                  Comparison                  Percent_Difference
    ______________________________________    __________________

    {'Partitioning versus Baseline'      }       {[85.2099]}    
    {'Backward Euler versus Baseline'    }       {[67.9931]}    
    {'Partitioning versus Backward Euler'}       {[53.7908]}

Simulation time on your machine may differ because simulation speed depends on machine processing power and the computational cost of concurrent processes.

The local fixed-step Partitioning and Backward Euler solvers are faster than the variable-step baseline solver. The Partitioning solver is typically, but not always, faster than the Backward Euler solver.

To compare the results, open the Simulink&reg Data Inspector.

% Get Simulink Data Inspector run IDs for
%    the last three runs
runIDs = Simulink.sdi.getAllRunIDs;
runBaseline = runIDs(end - 2);
runPartition = runIDs(end - 1);
runBackEuler = runIDs(end);

% Open the Simulink Data Inspector
Simulink.sdi.view

compBaselinePartition = Simulink.sdi.compareRuns(runBaseline,...
    runPartition);

Simulate a Simscape Model Using the Partitioning Solver

This example shows how to compare the speed and the accuracy of a simulation that uses the Partitioning solver to baseline results. It also shows how to compare the speeds of the Partitioning solver and the Backward Euler solver.

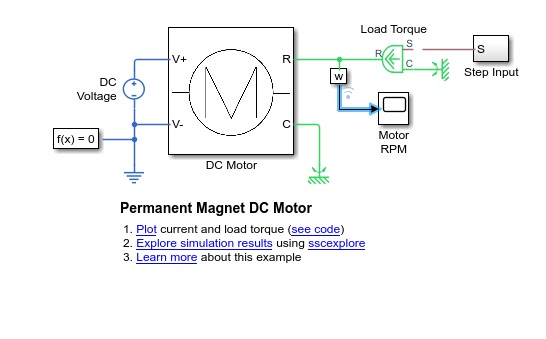
  1. Open the model. At the MATLAB® command prompt, enter the code.

     See Code

  2. To return all simulation outputs within a single Simulink.SimulationOutput object so that you can later compare simulation times, enable the single-output format of the sim command.

    model = 'PermanentMagnetDCMotor';
set_param(model,'ReturnWorkspaceOutputs', 'on')

  3. Enable the signal that goes to the Motor RPM scope block for Simulink® data logging and viewing with the Simulation Data Inspector.

     See Code

    The logging badge marks the signal in the model.

  4. Run timed simulations for each of these solvers:

    • Variable-step global solver, the original solver for the model

    • Fixed-step local Backward Euler solver

    • Fixed-step local Partitioning solver

     See Code

    compTimeDiffTable =

  3×2 table

         Solver         Sim_Duration
    ________________    ____________

    'Baseline'            [0.0319]  
    'Partitioning'        [0.0204]  
    'Backward Euler'      [0.0291]  

compPctDiffTable =

  3×2 table

                 Comparison                 Percent_Difference
    ____________________________________    __________________

    'Partitioning versus Baseline'              [35.9128]    
    'Backward Euler versus Baseline'            [ 8.6623]    
    'Partitioning versus Backward Euler'        [29.8349]

    Simulation time on your machine may differ because simulation speed depends on machine processing power and the computational cost of concurrent processes.

    The local fixed-step Partitioning and Backward Euler solvers are faster than the variable-step baseline solver. The Partitioning solver is typically, but not always, faster than the Backward Euler solver.

  5. To compare the results, open the Simulation Data Inspector.

     See Code

    To see the comparison, click Compare and then click Sensing 1.

    The first plot shows the overlay of the baseline and Partitioning solver simulation results. The second plot shows how they differ. The default tolerance for differences is 0. To determine if the accuracy of the results meet your requirements, you can adjust the relative, absolute, and time tolerances. For more information, see Compare Simulation Data.

Related Examples

More About