防抱死制动系统建模
此示例说明如何对一个简单的防抱死制动系统 (ABS) 进行建模。此模型对车辆在紧急制动情况下的动态行为进行仿真。该模型表示单个车轮,可以重复多次以创建多轮车辆的模型。
此模型使用 Simulink® 中的信号记录功能。该模型将信号记录到 MATLAB® 工作区,您可以在该工作区中查看和分析它们。查看 ModelingAnAntiLockBrakingSystemExample.m 文件中的代码,了解软件如何记录信号。
在 sldemo_absbrake 模型中,车轮速度是在名为 sldemo_wheelspeed_absbrake 的单独模型中计算的。然后使用 Model 模块引用该组件。顶层模型和引用模型都使用变步长求解器,因此 Simulink 将跟踪引用模型中的过零情况。
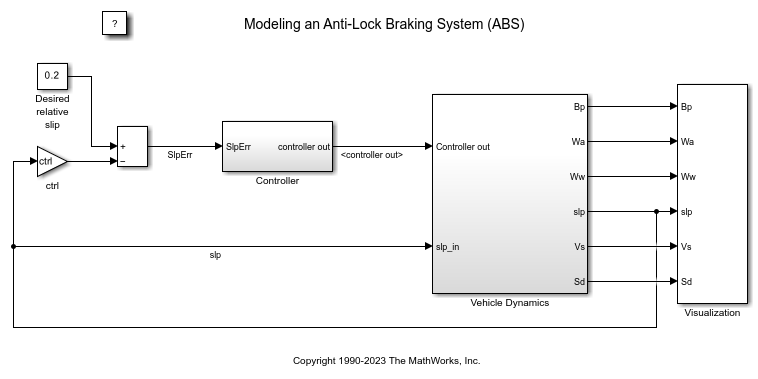
模型物理原理
车轮以初始角速度旋转,该初始角速度对应于施加制动之前的车速。该模型使用单独的积分器来计算车轮角速度和车速。该模型使用两种速度来计算滑动,滑动由方程 1 确定。请注意,车速以角速度表示。

方程 1



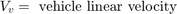

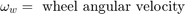
当车轮速度和车速相等时,滑动为零,当车轮抱死时,滑动等于 1。理想的滑动值是 0.2,这意味着车轮转数等于非制动条件下相同车速的转数的 0.8 倍。此值轮胎和道路之间的附着力最大,在可用摩擦力的作用下使停车距离最小。
模型分析
轮胎和路面之间的摩擦系数 mu 是滑动的经验函数,称为 mu-slip 曲线。软件通过使用 Simulink 查找表将 MATLAB 变量传递到模块图中创建了 mu-slip 曲线。该模型将摩擦系数 mu 乘以车轮承受的重量 W,得出作用在轮胎圆周上的摩擦力 Ff。Ff 除以车辆质量得出车辆减速度,模型对其进行积分获得车速。
此模型使用了理想的防抱死制动控制器,它根据实际滑动和期望滑动之间的误差使用 bang-bang 控制。期望的滑动设置为 mu-slip 曲线达到峰值时的滑动值,这是最小制动距离的最佳值。
在实际车辆中,滑动无法直接测量,因此这种控制算法并不实用。此示例使用算法在概念上说明这种仿真模型的构造。
双击 Wheel Speed 子系统将其打开。此子系统根据给定的车轮滑动、期望的车轮滑动和轮胎扭矩计算车轮角速度。

为了控制制动压力的变化率,该模型从期望的滑动量中减去实际滑动量,并将此信号馈入 bang-bang 控制(+1 或 -1,具体取决于误差的符号。此开/关速率通过一阶时滞,该时滞表示与制动系统的液压管路相关联的延迟。然后,该模型对滤波后的速率进行积分,以产生实际制动压力。所得信号乘以活塞面积和相对于车轮的半径 (Kf),即为施加到车轮上的制动扭矩。
该模型将车轮上的摩擦力乘以车轮半径 (Rr),得出路面作用于车轮的加速扭矩。从其减去制动扭矩,即可得出作用于车轮的净扭矩。将净扭矩除以车轮转动惯量 I,得出车轮加速度,然后将其积分以得到车轮速度。为了保持车轮速度和车速为正,模型使用有限积分器。
在 ABS 模式下仿真
在仿真选项卡上,点击运行以运行仿真。您也可以通过在 MATLAB 命令行窗口中输入 sim('sldemo_absbrake') 命令来运行仿真。在此仿真过程中,ABS 处于打开状态。



该模型将相关数据记录到 MATLAB 工作区中名为 sldemo_absbrake_output 的结构体。记录的信号有蓝色指示符。在本例中记录了 yout 和 slp。
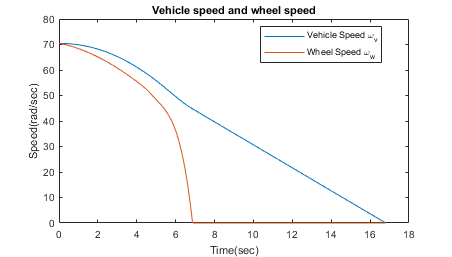
这些绘图显示默认参数的 ABS 仿真结果。第一个绘图显示车轮角速度和对应的车辆角速度。第二个图显示,车轮速度保持在车速以下而未启用抱死,车速在不到 15 秒内就变为零。系统会监测车轮加速度、车轮滑动率和制动压力。车轮滑动率用于确定车轮是否抱死。通过监控制动距离和制动压力来观察制动周期。
无 ABS 仿真
为了获得更有意义的结果,需要考虑没有 ABS 的情况下的车辆行为。在 MATLAB 命令行窗口中,设置模型变量 ctrl = 0。此设置将断开控制器与滑动反馈的连接,从而产生最大制动。
再次运行仿真以对不带 ABS 的制动进行仿真。
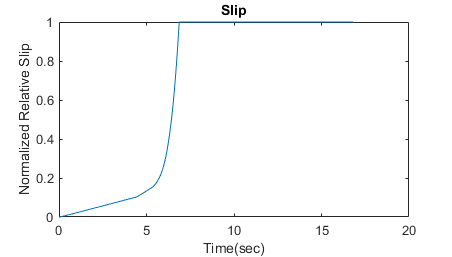

带 ABS 的制动与不带 ABS 的制动
在显示车速和车轮速度的图中,我们看到车轮在大约 7 秒后抱死。从该时刻起,制动应用于滑动曲线的次优部分。也就是说,当 slip = 1 时,正如滑动图所示,轮胎在路面上滑动太厉害,摩擦力下降。
此图显示这两种情况下车辆行驶的距离。如果没有 ABS,汽车会多滑行 100 英尺,完全停止所需的时间也会多出大约三秒。

扩展建模
此示例中的控制器是理想化的,但您可以使用任何控制算法来代替它,以评估您的系统的性能。要对提出的算法进行快速原型,您也可以使用 Simulink Coder™。
Simuink Coder 为控制器硬件生成和编译 C 代码,以在车辆中测试相关概念。此过程能够在开发周期的早期进行实际测试,从而大大减少证实新想法所需的时间。
对于硬件在环制动系统仿真,Simulink Coder 允许您生成实时 C 代码以删除 bang-bang 控制器,并在实时硬件上运行运动方程,以对车轮和车辆动力学进行仿真。然后,您可以通过将实际 ABS 控制器与运行所生成代码的实时硬件对接来测试该控制器。在此场景中,实时模型将向控制器发送车轮速度,控制器将向模型发送制动动作。