Simulink 中的定步长求解器
定步长求解器按固定时间间隔在从仿真开始到仿真结束的时间段内解算模型。间隔的大小称为步长。您可以指定步长,也可以让求解器选择步长。一般来说,步长越小,结果的准确性就越高,但也会增加仿真系统所需的时间。
定步长离散求解器
定步长离散求解器通过在当前时间上添加定步长来计算下一个仿真步骤的时间。最终仿真的准确性和时间长度取决于仿真所采取的步骤的大小:步长越小,结果越准确,但仿真所需的时间越长。默认情况下,Simulink® 选择步长,或者您可以自己选择步长。如果您选择默认设置自动,并且模型具有离散采样时间,则 Simulink 会将步长设置为模型的基本采样时间。否则,如果不存在离散速率,Simulink 将大小设置为仿真开始和停止时间之间的差值除以 50 的结果。
定步长连续求解器
定步长连续求解器与定步长离散求解器类似,通过在当前时间上添加固定大小的时间步长来计算下一个仿真时间。对于每个步骤,连续求解器使用数值积分来计算模型的连续状态的值。这些值是使用前一时间步的连续状态以及当前时间步和前一时间步之间的中间点(小步)的状态导数来计算的。
注意
对于不包含状态或仅包含离散状态的模型,Simulink 使用定步长离散求解器,即使您为该模型指定了定步长连续求解器。
Simulink 提供两种类型的定步长连续求解器 - 显式和隐式。
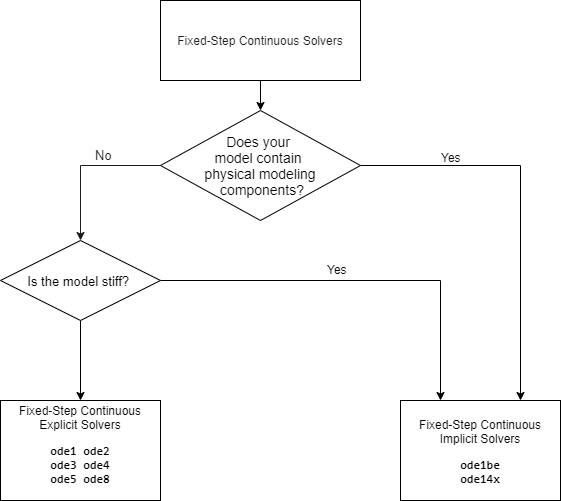
这两种类型之间的区别在于速度和稳定性。隐式求解器每步需要的计算量比显式求解器要多,但稳定性也更高。因此,Simulink 提供的隐式定步长求解器比定步长显式求解器更适合求解刚性系统。有关显式和隐式求解器的比较,请参阅显式与隐式连续求解器。
定步长连续显式求解器
显式求解器将下一个时间步的状态值计算为状态和状态导数的当前值的显式函数。定步长显式求解器在数学上表示为:
,其中
x 是状态。
Dx 是一个依赖于求解器的函数,用于估计状态导数。
h 是步长。
n 表示当前时间步长。
Simulink 提供了一组定步长连续显式求解器。求解器在计算模型状态导数时使用的具体数值积分技术有所不同。该表列出了每个求解器及其使用的积分技术。该表按照所使用的积分方法的计算复杂度的顺序列出了求解器,从最不复杂(ode1)到最复杂(ode8)。
| 求解器 | 积分方法 | 准确度顺序 |
|---|---|---|
| 欧拉方法 | 第一个 |
| Heun 方法 | 第二 |
| 博加基-尚派恩公式 | 第三 |
| 四阶龙格-库塔(RK4)公式 | 第四 |
| Dormand-Prince(RK5)公式 | 第五 |
| Dormand-Prince RK8(7)公式 | 第八 |
这些求解器都没有错误控制机制。因此,仿真的准确性和持续时间直接取决于求解器所采取的步骤的大小。随着步长的减小,结果会变得更加准确,但仿真所需的时间也会更长。此外,对于任何给定的步长,求解器的阶数越高,仿真结果越准确。
如果为模型指定定步长求解器类型,则默认情况下,Simulink 会选择 FixedStepAuto 求解器。然后,自动求解器选择一个适当的定步长求解器,该求解器可以以适度的计算工作量处理连续和离散状态。与离散求解器一样,如果模型具有离散速率(采样时间),则 Simulink 默认将步长设置为模型的基本采样时间。如果模型没有离散速率,Simulink 会自动使用仿真总持续时间除以 50 的结果。因此,求解器在每次仿真时都会采取一步,其中 Simulink 必须以其指定的采样率更新模型的离散状态。但是,它不能保证默认求解器准确计算模型的连续状态。因此,您可能需要选择另一个求解器、不同的定步长或两者来实现可接受的精度和可接受的仿真时间。
定步长连续隐式求解器
隐式求解器将下一个时间步的状态计算为当前时间步的状态和下一个时间步的状态导数的隐式函数,如下式所述。
Simulink 提供了两个定步长隐式求解器:ode14x 和 ode1be。该求解器结合使用牛顿法和当前值外推法来计算下一个时间步的状态值。您可以指定牛顿法迭代次数和求解器用于计算模型状态的下一个值的外推阶数。请参阅 定步长(基础采样时间)。您选择的迭代次数越多、外推阶数越高,获得的精度就越高。然而,同时每步长也会产生更大的计算负担。