Linearize Multirate Models

You can linearize a Simulink^® model that contains blocks with different sample times using Simulink Control Design™ software. By default, the linearization tools:

Convert sample times using a zero-order hold conversion method.
Create a linearized model with a sample time equal to the largest sample time of the blocks on the linearization path.

You can change either of these behaviors by specifying linearization options, which affects the linearization result.

Change Sample Time of Linear Model

By default, the software sets the sample time to the least common multiple of the nonzero sample times in the model. At this rate, down-sampling is exact for all of the rates in the model. If the default sample time is not appropriate for your application, you can specify a different sample time.

To specify the sample time of the linear model in the Model Linearizer:

On the Linear Analysis tab, click More Options.
In the Options for exact linearization dialog box, on the Linearization tab, in the Enter sample time (sec) field, specify the sample time. You can specify any of the following values.
- -1 — Set the sample time to the least common multiple of the nonzero sample times in the model.
- 0 — Create a continuous-time model.
- Positive scalar — Use the specified value for the sample time.

To specify the sample time of the linear model at the command line, create a linearizeOptions option set, and set the SampleTime option.

opt = linearizeOptions;
opt.SampleTime = 0.01;

You can then use this option set with linearize or slLinearizer.

Change Linearization Rate Conversion Method

When you linearize models with multiple sample times, such as a discrete controller with a continuous plant, the software uses a rate conversion algorithm to create a single-rate linear model. The default rate conversion method is zero-order hold.

To specify the rate conversion method in the Model Linearizer:

On the Linear Analysis tab, click More Options.

In the Options for exact linearization dialog box, on the Linearization tab, in the Choose rate conversion method drop-down list, select one of the following rate conversion methods.

Rate Conversion Method	When to Use
`Zero-Order Hold`	You need exact discretization of continuous dynamics in the time domain for staircase inputs.
`Tustin`	You need good frequency-domain matching between a continuous-time system and the corresponding discretized system, or between an original system and a resampled system.
`Tustin with Prewarping`	You need good frequency-domain matching at a particular frequency between a continuous-time system and the corresponding discretized system, or between an original system and the resampled system.
`Upsampling when possible, Zero-Order Hold otherwise` `Upsampling when possible, Tustin otherwise` `Upsampling when possible, Tustin with Prewarping otherwise`	Upsample discrete states when possible to ensure gain and phase matching of upsampled dynamics. You can only upsample when the new sample time is an integer multiple of the sample time of the original system. Otherwise, the software uses the alternate rate conversion method.

If you select either of the following rate conversion methods:
- Tustin with Prewarping
- Upsampling when possible, Tustin with Prewarping otherwise
then, in the Enter prewarp frequency field, specify the prewarp frequency.

To specify the rate conversion method at the command line, create a linearizeOptions object, and set the RateConversionMethod and PreWarpFreq options.

opt = linearizeOptions;
opt.RateConversionMethod = 'prewarp';
opt.PreWarpFreq = 100;

You can then use this options object with linearize or slLinearizer.

Note

If you use a rate conversion method other than zero-order hold, the converted states no longer have the same physical meaning as the original states. As a result, the state names in the resulting LTI system are '?'.

Multirate Linearization Algorithm

Open Script

This example demonstrates the algorithm that Simulink® Control Design™ software uses to linearize a multirate nonlinear Simulink model.

To illustrate the concepts, the example shows the linearization process using Control System Toolbox™ functions. Then, the same process is repeated using the linearize function.

The scdmrate Simulink model contains five blocks with various sample times. All linear systems in this model are in zero-pole-gain format.

sysC - Continuous-time linear time-invariant (LTI) system
Integrator - Continuous-time integrator
sysTs1 - Discrete-time LTI system with a sample time of 0.01 seconds
sysTs2 - Discrete-time LTI system with a sample time of 0.025 seconds
Zero-Order Hold - Block that samples the incoming signal at 0.01 seconds

sysC = zpk(-2,-10,0.1);
Integrator = zpk([],0,1);
sysTs1 = zpk(-0.7463,[0.4251 0.9735],0.2212,0.01);
sysTs2 = zpk([],0.7788,0.2212,0.025);

View the scdmrate model.

open_system('scdmrate')

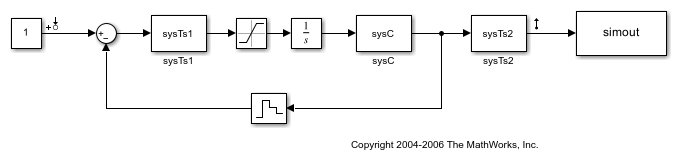
In this example, you linearize the model between the output of the Constant block and the output of the sysTs2 block.

Linearize Individual Blocks

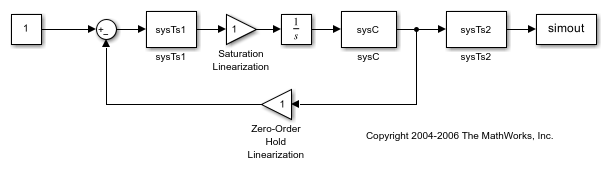
The first step of the linearization process is to linearize each block in the model. The linearization for the Saturation and Zero-Order Hold blocks is a gain of 1. Since the LIT blocks are already linear, they are unchanged.

View the updated model with the linearized blocks.

open_system('scdmratestep1')

Perform Rate Conversion

Since the blocks in the model use different sample times, to create a single-rate linearized model for the system you must first convert the various sample rates to a representative single rate.

The linearize function uses an iterative rate conversion method. The iterations begin with the least common multiple of the sample times in the model. In this example, the sample times are 0, 0.01, and 0.025 seconds, which yields a least common multiple of 0.05.

The first rate-conversion iteration resamples the combination of blocks with the fastest sample rate at the next fastest rate. In this example, the first iteration converts the combination of the linearized continuous-time blocks, sysC and Integrator, to a sample time of 0.01 using a zero-order hold continuous-to-discrete conversion.

sysC_Ts1 = c2d(sysC*Integrator,0.01);

The blocks sysC and Integrator are now replaced by sysC_Ts1.

open_system('scdmratestep2')

The next iteration converts all the blocks with a sample time of 0.01 to a sample time of 0.025. In this example, all the blocks with a sample rate of 0.01 form a closed-loop system. Therefore, before converting their sample rate, the linearization algorithm computes the response of the closed-loop system.

sysCL = feedback(sysTs1*sysC_Ts1,1);

Next, a zero-order hold method converts the closed-loop system from a sample time of 0.01 seconds to 0.025 seconds.

sysCL_Ts2 = d2d(sysCL,0.025);

The system sysCL_Ts2 then replaces the feedback loop in the model.

open_system('scdmratestep3')

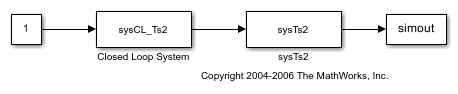
The final iteration resamples the combination of the closed-loop system and the sysTs2 block from a sample time of 0.025 seconds to 0.05 seconds.

sys1 = d2d(sysCL_Ts2*sysTs2,0.05)

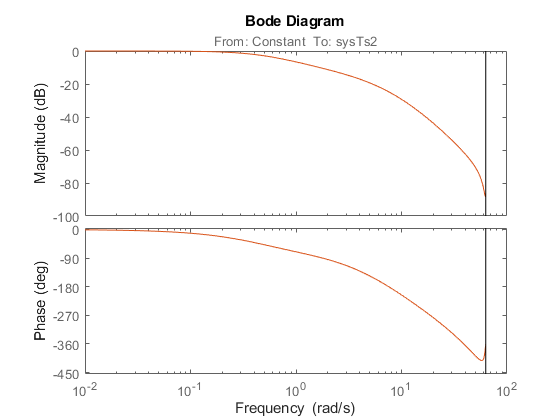
sys1 =
 
   0.0001057 (z+22.76) (z+0.912) (z-0.9048) (z+0.06495)
  -------------------------------------------------------
  (z-0.01373) (z-0.6065) (z-0.6386) (z-0.8588) (z-0.9754)
 
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.

Linearize Model Using Simulink Control Design Functions

The linearize function implements this iterative process for linearizing multirate models.

To linearize the model, first specify the linearization input and output points.

io(1) = linio('scdmrate/Constant',1,'input');
io(2) = linio('scdmrate/sysTs2',1,'openoutput');

Linearize the model and convert the resulting state-space model to zero-pole-gain format.

sys2 = zpk(linearize('scdmrate',io))

sys2 =
 
  From input "Constant" to output "sysTs2":
   0.0001057 (z+22.76) (z+0.912) (z-0.9048) (z+0.06495)
  -------------------------------------------------------
  (z-0.6065) (z-0.6386) (z-0.8588) (z-0.9754) (z-0.01373)
 
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.

This model matches the model computed manually.

bode(sys1,sys2)