连续-离散转换方法

Control System Toolbox™ 提供了多种离散化方法和插值方法，用于在连续时间与离散时间之间转换动态系统模型，以及重采样离散时间模型。一些方法倾向于在原始系统和转换后的系统之间提供更好的频域匹配，而其他方法则提供更好的时域匹配。使用下表来帮助选择最符合您的应用需求的方法。

离散化方法	适用场景
零阶保持	您希望在时域中对阶梯输入进行精确离散化。
一阶保持	您希望在时域中对分段线性输入进行精确离散化。
冲激不变映射（仅限连续到离散转换）	您希望在时域中对冲激序列输入进行精确离散化。
突斯汀逼近	您希望连续时间模型与离散时间模型在频域中有良好的匹配。您的模型在某个特定频率下有重要的动态特性。
零极点匹配等效法	您拥有的是 SISO 模型。您希望连续时间模型与离散时间模型在频域中有良好的匹配。
最小二乘法（仅限连续到离散转换）	您拥有的是 SISO 模型。您希望连续时间模型与离散时间模型在频域中有良好的匹配。您希望捕捉系统快速动态特性但必须使用较大的采样时间。

关于如何在命令行中指定转换方法的信息，请参阅 c2d、d2c 和 d2d。您可以在实时编辑器中使用转换模型速率任务以交互方式试验不同的离散化方法。

零阶保持

零阶保持 (ZOH) 方法可在时域中对阶梯输入实现连续时间系统与离散时间系统之间的精确匹配。

以下模块图说明了连续时间线性模型 H(s) 的零阶保持离散化 H_d(z)。

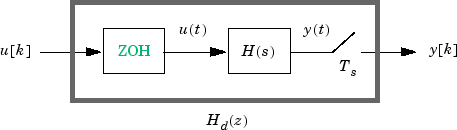
ZOH 模块通过在一个采样周期内保持每个采样值 u(k) 恒定，来生成连续时间输入信号 u(t)：

$u (t) = u [k], k T_{s} \leq t \leq (k + 1) T_{s}$

信号 u(t) 是连续系统 H(s) 的输入。输出 y[k] 是对 y(t) 每隔 T_s 秒进行采样的结果。

反之，如果给定的是离散系统 H_d(z)，d2c 会生成一个连续系统 H(s)。H(s) 的 ZOH 离散化结果与 H_d(z) 一致。

ZOH 离散到连续转换具有以下限制：

d2c 无法转换在 z = 0 处有极点的 LTI 模型。
对于具有负实极点的离散时间 LTI 模型，ZOH d2c 转换会生成更高阶的连续系统。模型阶数增加是因为 z 域中的负实极点会映射到 s 域中的纯虚数值。这种映射会导致连续时间模型具有复数数据。为避免此问题，软件会在 s 域中引入一对复共轭极点。有关示例，请参阅Convert Discrete-Time System to Continuous Time。

具有时滞的系统的 ZOH 方法

您可以使用 ZOH 方法对具有时滞的 SISO 或 MIMO 连续时间模型进行离散化。对于具有输入延迟、输出延迟或传输延迟的系统，ZOH 方法能实现精确离散化。

对于具有内部延迟（反馈环中的延迟）的系统，ZOH 方法仅能实现逼近离散化。下图显示了一个具有内部延迟的系统。

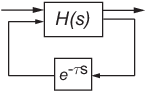
对于这类系统，c2d 通过以下步骤计算逼近 ZOH 离散化：

将时滞 τ 分解为 $τ = k T_{s} + ρ$ ，其中 $0 \leq ρ < T_{s}$ 。
将分数时滞 $ρ$ 吸收到 H(s) 中。
将 H(s) 离散化为 H(z)。
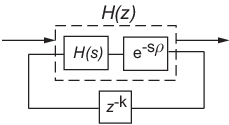
将时滞的整数部分 kT_s 表示为内部离散时滞 z^–k。最终离散化模型如下图所示：

一阶保持

一阶保持 (FOH) 方法可在时域中对分段线性输入实现连续时间系统与离散时间系统之间的精确匹配。

FOH 与 ZOH 的区别在于其底层保持机制。要将输入采样值 u[k] 转换为连续输入 u(t)，FOH 采用采样值间的线性插值：

$u (t) = u [k] + \frac{t - k T_{s}}{T_{s}} (u [k + 1] - u [k]), k T_{s} \leq t \leq (k + 1) T_{s}$

通常，对于由平滑输入驱动的系统，此方法比 ZOH 更精确。

此 FOH 方法不同于标准因果 FOH，更准确地说应称为三角逼近（请参阅[2]，第 228 页）。该方法也被称为“斜坡不变逼近”。

具有时滞的系统的 FOH 方法

您可以使用 FOH 方法对具有时滞的 SISO 或 MIMO 连续时间模型进行离散化。FOH 方法处理时滞的方式与 ZOH 方法相同。请参阅具有时滞的系统的 ZOH 方法。

冲激不变映射

冲激不变映射生成的离散时间模型，其冲激响应与原连续时间系统的冲激响应相同。例如，比较一阶连续系统与冲激不变离散化后的冲激响应：

G = tf(1,[1,1]);
Gd1 = c2d(G,0.01,'impulse');
impulse(G,Gd1)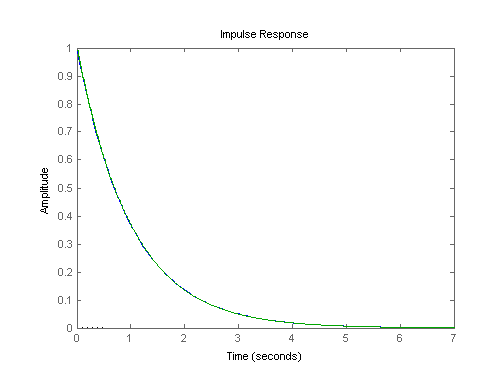

从冲激响应图中可观察到，连续系统与离散化系统的冲激响应完全匹配。

具有时滞的系统的冲激不变映射

您可以使用冲激不变映射对具有时滞的 SISO 或 MIMO 连续时间模型进行离散化，但该方法不支持具有内部延迟的 ss 模型。对于受支持的模型，冲激不变映射可实现时滞的精确离散化。

突斯汀逼近

突斯汀逼近（又称双线性逼近）可使连续时间系统与离散化系统实现最佳频域匹配。此方法通过以下逼近关系关联 s 域与 z 域的传递函数：

$z = e^{s T_{s}} \approx \frac{1 + s T_{s} / 2}{1 - s T_{s} / 2} .$

在 c2d 转换中，连续传递函数 H(s) 的离散化结果 H_d(z) 为：

$H_{d} (z) = H (s^{'}), s^{'} = \frac{2}{T_{s}} \frac{z - 1}{z + 1}$

类似地，d2c 转换基于以下逆对应关系：

$H (s) = H_{d} (z^{'}), z^{'} = \frac{1 + s T_{s} / 2}{1 - s T_{s} / 2}$

当您使用突斯汀方法转换状态空间模型时，原始模型的状态不会被保留。状态变换取决于状态空间矩阵以及系统是否具有时滞。例如，对于无时滞的显式连续时间模型（E = I），离散化模型的状态向量 w[k] 与连续时间模型的状态向量 x(t) 存在以下关系：

$w [k T_{s}] = (I - A \frac{T_{s}}{2}) x (k T_{s}) - \frac{T_{s}}{2} B u (k T_{s}) = x (k T_{s}) - \frac{T_{s}}{2} (A x (k T_{s}) + B u (k T_{s})) .$

其中，T_s 是离散时间模型的采样时间。A 和 B 是连续时间模型的状态空间矩阵。

突斯汀逼近对在 z = –1 处有极点的系统无定义，且对极点在 z = –1 附近的系统表现出病态。

具有频率预修正的突斯汀逼近

如果您的系统在特定频率下具有重要的动态特性，并且希望变换后保留这些动态特性，则可以使用具有频率预修正的突斯汀方法。此方法可确保连续时间系统与离散时间系统在预修正频率下的响应匹配。

具有频率预修正的突斯汀逼近使用以下变量变换：

$H_{d} (z) = H (s^{'}), s^{'} = \frac{ω}{\tan (ω T_{s} / 2)} \frac{z - 1}{z + 1}$

该变量变换可确保连续时间系统与离散时间系统在预修正频率 ω 下的频率响应匹配，原因是存在以下对应关系：

$H (j ω) = H_{d} (e^{j ω T_{s}})$

具有时滞的系统的突斯汀逼近

您可以使用突斯汀逼近对具有时滞的 SISO 或 MIMO 连续时间模型进行离散化。

默认情况下，突斯汀方法会将任意时滞四舍五入到最接近的采样时间倍数。因此，对于任意时滞 tau，时滞的整数部分 k*Ts 会映射为离散化模型中 k 个采样周期的时滞。该方法会忽略剩余的分数时滞 tau - k*Ts。

您可以通过指定阶数的离散全通滤波器（蒂兰滤波器）逼近时滞的分数部分。为此，可使用 c2dOptions 的 ThiranOrder 选项。有关示例，请参阅Improve Accuracy of Discretized System with Time Delay。

为理解突斯汀方法如何处理具有时滞的系统，假设有以下 SISO 状态空间模型 G(s)。该模型包含输入延迟 τ_i、输出延迟 τ_o 和内部延迟 τ。

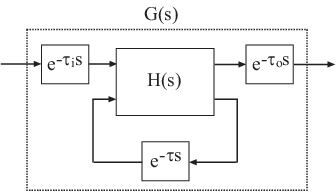
下图显示了使用突斯汀方法对 G(s) 进行离散化的一般结果。

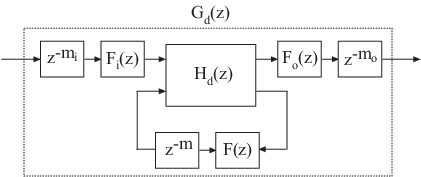
默认情况下，c2d 会将时滞转换为纯整数时滞。c2d 命令通过将每个时滞四舍五入到采样时间 T_s 的最接近倍数来计算整数时滞。因此，在默认情况下，m_i = round(τ_i/T_s), m_o = round(τ_o/T_s), and m = round(τ/T_s).。同时，在该情况下，F_i(z) = F_o(z) = F(z) = 1。

如果将 ThiranOrder 设置为非零值，c2d 会通过蒂兰滤波器 F_i(z)、F_o(z) 和 F(z) 逼近时滞的分数部分。

蒂兰滤波器会为模型增加附加状态。每个时滞的最大附加状态数为 ThiranOrder。

例如，对于输入延迟 τ_i，蒂兰滤波器 F_i(z) 的阶数为：

order(F_i(z)) = max(ceil(τ_i/T_s), ThiranOrder).

如果 ceil(τ_i/T_s) < ThiranOrder，则蒂兰滤波器 F_i(z) 会逼近整个输入延迟 τ_i。如果 ceil(τ_i/T_s) > ThiranOrder，则蒂兰滤波器仅逼近输入延迟的一部分。此时，c2d 会将输入延迟的剩余部分表示为单位延迟链 z^–m_i，其中：

m_i = ceil(τ_i/T_s) – ThiranOrder

c2d 会以类似方式使用蒂兰滤波器和 ThiranOrder 来逼近输出延迟 τ_o 和内部延迟 τ。

当使用突斯汀方法对 tf 和 zpk 模型进行离散化时，c2d 首先将每个通道的所有输入延迟、输出延迟和传输延迟聚合为单个传输延迟 τ_TOT，然后 c2d 按照处理 ss 模型中各类时滞的方式，将 τ_TOT 逼近为一个蒂兰滤波器和一条单位延迟链。

有关蒂兰滤波器的详细信息，请参阅 thiran 参考页和[4]。

零极点匹配等效法

零极点匹配等效法（即通过计算零极点匹配等效模型实现转换的方法）仅适用于 SISO 系统。连续系统与离散化系统具有匹配的 DC 增益。它们的零极点通过以下变换关联：

$z_{i} = e^{s_{i} T_{s}}$

其中：

z_i 是离散时间系统的第 i 个极点或零点。
s_i 是连续时间系统的第 i 个极点或零点。
T_s 是采样时间。

有关详细信息，请参阅[2]。

具有时滞的系统的零极点匹配法

您可以使用零极点匹配法对具有时滞的 SISO 连续时间模型进行离散化，但该方法不支持具有内部延迟的 ss 模型。零极点匹配法处理时滞的方式与突斯汀逼近相同。请参阅具有时滞的系统的突斯汀逼近。

最小二乘法

最小二乘法通过向量拟合优化方法，最小化连续时间系统与离散时间系统在奈奎斯特频率范围内的频率响应误差。当您希望捕捉系统快速动态特性但必须使用较大的采样时间时（例如计算资源有限的场景），此方法非常实用。

此方法仅受 c2d 函数支持，且仅适用于 SISO 系统。

与突斯汀逼近和零极点匹配法类似，最小二乘法能使原始连续时间系统与转换后的离散时间系统的频率响应实现良好匹配。但使用最小二乘法时：

如果采用与突斯汀逼近或零极点匹配法相同的采样时间，连续时间与离散时间系统的频率响应差异更小。
如果采用比突斯汀逼近或零极点匹配法更慢的采样时间，仍能得到满足要求的结果。这在计算资源有限时非常有用，因为较慢的采样时间意味着处理器的工作量更小。

参考

[1] Åström, K.J. and B. Wittenmark, Computer-Controlled Systems: Theory and Design, Prentice-Hall, 1990, pp. 48-52.

[2] Franklin, G.F., Powell, D.J., and Workman, M.L., Digital Control of Dynamic Systems (3rd Edition), Prentice Hall, 1997.

[3] Smith, J.O. III, "Impulse Invariant Method", Physical Audio Signal Processing, August 2007. https://www.dsprelated.com/dspbooks/pasp/Impulse_Invariant_Method.html.

[4] T. Laakso, V. Valimaki, "Splitting the Unit Delay", IEEE Signal Processing Magazine, Vol. 13, No. 1, p.30-60, 1996.