c2d

将模型从连续时间转换为离散时间

全页折叠

语法

sysd = c2d(sysc,Ts)

sysd = c2d(sysc,Ts,method)

sysd = c2d(sysc,Ts,opts)

[sysd,G] = c2d(___)

说明

sysd = c2d(sysc,Ts) 离散化连续时间动态系统模型 sysc，对输入使用零阶保持并使用 Ts 的采样时间。

示例

sysd = c2d(sysc,Ts,method) 指定离散化方法。

示例

sysd = c2d(sysc,Ts,opts) 指定离散化的附加选项。

示例

[sysd,G] = c2d(___)（其中 sysc 是状态空间模型）返回一个矩阵 G，该矩阵将状态空间模型的连续初始条件 x₀ 和 u₀ 映射到离散时间初始状态向量 x[0].

示例

全部折叠

离散化传递函数

打开实时脚本

将以下连续时间传递函数离散化：

$H (s) = e^{- 0.3 s} \frac{s - 1}{s^{2} + 4 s + 5} .$

此系统的输入延迟为 0.3 秒。使用采样时间 Ts = 0.1 秒的三角形（一阶保持）逼近对系统进行离散化。

H = tf([1 -1],[1 4 5],'InputDelay', 0.3); 
Hd = c2d(H,0.1,'foh');

比较连续时间和离散系统的阶跃响应。

step(H,'-',Hd,'--')

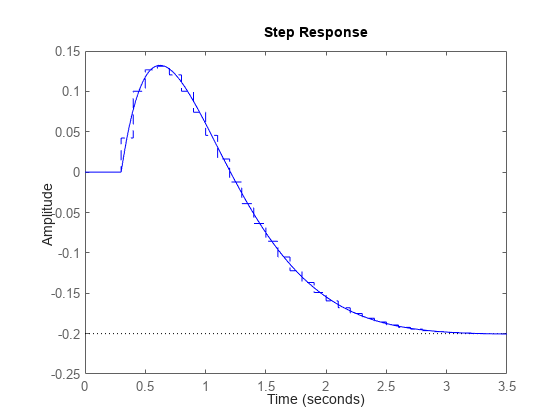
MATLAB figure

通过将小数延迟吸收到系数中来离散化模型

打开实时脚本

对输入使用零阶保持并使用 10Hz 采样率，离散化以下延迟传递函数。

$H (s) = e^{- 0.25 s} \frac{10}{s^{2} + 3 s + 10} .$

h = tf(10,[1 3 10],'IODelay',0.25); 
hd = c2d(h,0.1)

hd =
 
           0.01187 z^2 + 0.06408 z + 0.009721
  z^(-3) * ----------------------------------
                 z^2 - 1.655 z + 0.7408
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

在此示例中，离散化模型 hd 有三个采样周期的延迟。离散化算法将残差半周期延迟纳入 hd 的系数中。

比较连续时间模型和离散化模型的阶跃响应。

step(h,'--',hd,'-')

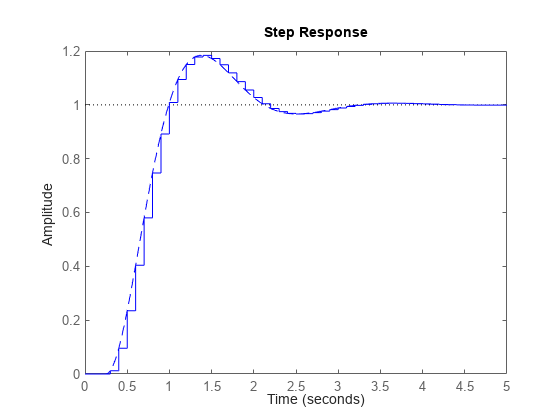
MATLAB figure

使用逼近的小数延迟离散化模型

自 R2024a 起

打开实时脚本

创建具有两个状态和一个输入延迟的连续时间状态空间模型。

sys = ss(tf([1,2],[1,4,2]));
sys.InputDelay = 2.7

sys =
 
  A = 
       x1  x2
   x1  -4  -2
   x2   1   0
 
  B = 
       u1
   x1   2
   x2   0
 
  C = 
        x1   x2
   y1  0.5    1
 
  D = 
       u1
   y1   0
 
  Input delays (seconds): 2.7 
 
Continuous-time state-space model.
Model Properties

使用突斯汀离散化方法和蒂兰滤波器对模型进行离散化，以对小数延迟进行建模。采样时间 Ts = 1 秒。

opt = c2dOptions('Method','tustin','ThiranOrder',3);
sysd1 = c2d(sys,1,opt)

sysd1 =
 
  A = 
            x1       x2
   x1  -0.4286  -0.5714
   x2   0.2857   0.7143
 
  B = 
           u1
   x1  0.5714
   x2  0.2857
 
  C = 
           x1      x2
   y1  0.2857  0.7143
 
  D = 
           u1
   y1  0.2857
 
  (values computed with all internal delays set to zero)

  Internal delays (sampling periods): 1  1  1 
 
Sample time: 1 seconds
Discrete-time state-space model.
Model Properties

默认情况下，该函数将额外延迟建模为离散化模型中的内部延迟。要将额外延迟建模为离散化模型中的状态，请将 c2dOptions 的 DelayModeling 选项设置为 'state'。

opt2 = c2dOptions('Method','tustin','ThiranOrder',3,'DelayModeling','state');
sysd2 = c2d(sys,1,opt2)

sysd2 =
 
  A = 
              x1         x2         x3         x4         x5
   x1    -0.4286    -0.5714   -0.00265    0.06954      2.286
   x2     0.2857     0.7143  -0.001325    0.03477      1.143
   x3          0          0    -0.2432     0.1449    -0.1153
   x4          0          0       0.25          0          0
   x5          0          0          0      0.125          0
 
  B = 
             u1
   x1  0.002058
   x2  0.001029
   x3         8
   x4         0
   x5         0
 
  C = 
              x1         x2         x3         x4         x5
   y1     0.2857     0.7143  -0.001325    0.03477      1.143
 
  D = 
             u1
   y1  0.001029
 
Sample time: 1 seconds
Discrete-time state-space model.
Model Properties

离散化模型现在包含对应于三阶 Thiran 滤波器的三个附加状态 x3、x4 和 x5。由于时滞除以采样时间为 2.7，因此三阶 Thiran 滤波器 ('ThiranOrder' = 3) 可以逼近整个时滞。

离散化辨识的模型

此示例使用:

System Identification Toolbox System Identification Toolbox

打开实时脚本

估计连续时间传递函数，并将其离散化。

load iddata1
sys1c = tfest(z1,2);
sys1d = c2d(sys1c,0.1,'zoh');

估计二阶离散时间传递函数。

sys2d = tfest(z1,2,'Ts',0.1);

比较离散化连续时间传递函数模型 sys1d 和直接估计的离散时间模型 sys2d 的响应。

compare(z1,sys1d,sys2d)

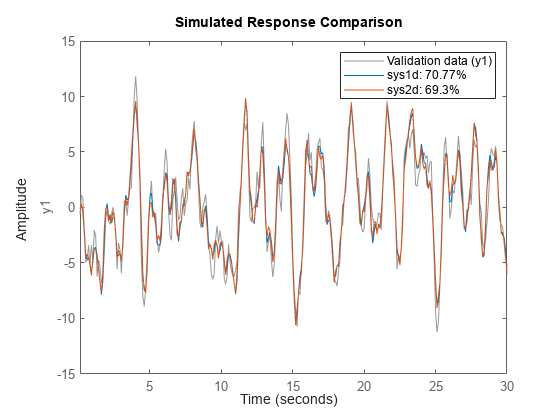
Figure contains an axes object. The axes object with ylabel y1 contains 3 objects of type line. These objects represent Validation data (y1), sys1d: 70.77%, sys2d: 69.3%.

这两个系统几乎完全相同。

构建预测器模型

此示例使用:

打开实时脚本

对一个辨识的状态空间模型进行离散化，以构建其响应的向前一步预测器。

使用估计数据创建一个辨识的连续时间状态空间模型。

load iddata2
sysc = ssest(z2,4);

预测 sysc 的超前 1 步预测响应。

predict(sysc,z2)

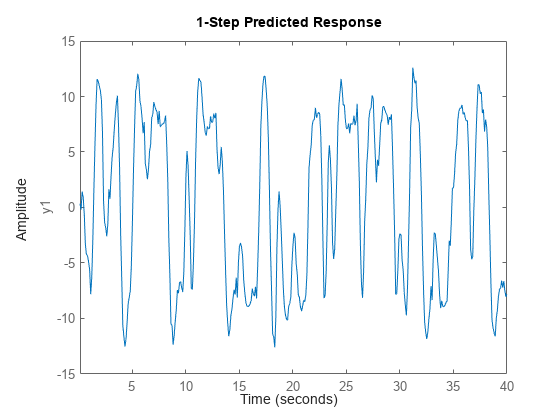
Figure contains an axes object. The axes object with ylabel y1 contains an object of type line. These objects represent Validation data (y1), sysc.

离散化该模型。

sysd = c2d(sysc,0.1,'zoh');

从离散化模型 sysd 构建一个预测器模型。

[A,B,C,D,K] = idssdata(sysd);
Predictor = ss(A-K*C,[K B-K*D],C,[0 D],0.1);

Predictor 是双输入模型，它使用测量的输出和输入信号 ([z1.y z1.u]) 来计算 sysc 的超前 1 步预测响应。

仿真预测器模型以获得与 predict 命令相同的响应。

lsim(Predictor,[z2.y,z2.u])

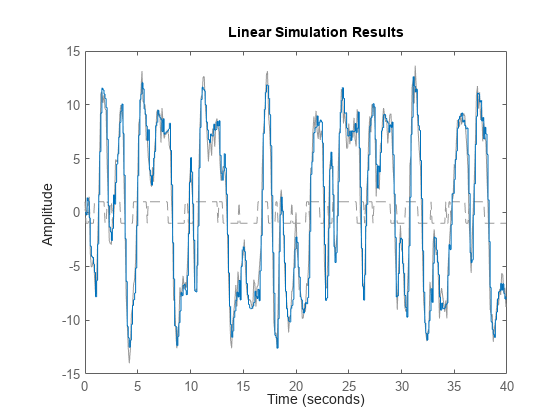
MATLAB figure

预测器模型的仿真给出与 predict(sysc,z2) 相同的响应。

输入参数

全部折叠

`sysc` — 连续时间动态系统
动态系统模型

连续时间模型，指定为动态系统模型，如 tf、ss 或 zpk。sysc 不能为频率响应数据模型。sysc 可以是 SISO 或 MIMO 系统，不同之处在于 'matched' 离散化方法仅支持 SISO 系统。

sysc 可以有输入/输出或内部时滞；然而，'matched'、'impulse' 和 'least-squares' 方法不支持具有内部时滞的状态空间模型。

以下辨识的线性系统无法直接离散化：

idgrey 模型，其 FunctionType 是 'c'。首先转换为 idss 模型。
idproc 模型。首先转换为 idtf 或 idpoly 模型。

`Ts` — 采样时间
正标量

采样时间，指定为正标量，表示生成的离散时间系统的采样周期。Ts 以 TimeUnit 为单位，后者是 sysc.TimeUnit 属性。

`method` — 离散化方法
`'zoh'` (默认) | `'foh'` | `'impulse'` | `'tustin'` | `'matched'` | `'least-squares'` | `'damped'`

离散化方法，指定为以下值之一：

'zoh' - 零阶保持（默认值）。假定控制输入在采样时间周期 Ts 内是分段常量。
'foh' - 三角形逼近（修正一阶保持）。假定控制输入在采样时间周期 Ts 内是分段线性值。
'impulse' - 冲激不变离散化
'tustin' - 双线性（突斯汀）方法。要指定在此方法中使用频率预修正（以前称为 'prewarp' 方法），请使用 c2dOptions 的 PrewarpFrequency 选项。
'matched' - 零极点匹配法
'least-squares' - 最小二乘法
'damped' - 仅基于 sparss 模型的 TRBDF2 公式的阻尼突斯汀逼近。

有关每种转换方法的算法的信息，请参阅Continuous-Discrete Conversion Methods。

`opts` — 离散化选项
`c2dOptions` 对象

离散化选项，指定为 c2dOptions 对象。例如，将预修正频率、Thiran 滤波器的阶数或离散化方法指定为选项。

输出参量

全部折叠

`sysd` — 离散时间模型
动态系统模型

离散时间模型，以与输入系统 sysc 相同类型的动态系统模型形式返回。

当 sysc 是辨识的 (IDLTI) 模型时，sysd：

同时包括 sysc 的测量组件和噪声。连续时间辨识模型 sysc 的新信息方差 λ，存储在其 NoiseVariance 属性中，解释为噪声频谱的频谱密度的强度。因此 sysd 中的噪声方差为 λ/Ts。
不包括 sysc 的估计参数协方差。如果要在离散化模型时转换协方差，请使用 translatecov。

`G` — 状态空间模型的连续初始条件到离散时间初始状态向量的映射
矩阵

状态空间模型 sysc 的连续时间初始条件 x₀ 和 u₀ 到离散时间初始状态向量 x[0] 的映射，以矩阵形式返回。初始条件到初始状态向量的映射如下：

$x [0] = G \cdot [\begin{matrix} x_{0} \\ u_{0} \end{matrix}]$

对于具有时滞的状态空间模型，c2d 用零填充矩阵 G 以考虑离散化这些延迟所引入的额外状态。有关离散化系统中时滞建模的讨论，请参阅Continuous-Discrete Conversion Methods。

版本历史记录

在 R2006a 之前推出

全部展开

R2024a: 在转换期间不添加额外状态

c2d 命令在对额外延迟进行建模时不再添加额外状态。默认情况下，c2d 现在使用内部延迟并返回具有相同状态数目的离散化模型。这会使行为更加可预测，并简化从连续时间到离散时间的初始状态映射。

要还原到 R2024a 之前的旧行为，请使用 c2dOptions 创建一个选项集并将 DelayModeling 设置为 "state"。

R2024a: 支持 `mechss` 模型

您现在可以使用双线性突斯汀逼近方法离散化 mechss 模型。对于 mechss 模型，'tustin' 方法计算突斯汀离散化的二阶形式。这等效于将突斯汀应用于 sparss 模型的一阶 mechss 等效项。

R2024a: 支持具有偏移量和其他改进的模型

您现在可以使用 c2d 离散化具有偏移量的模型，例如网格线性参数变化模型。

此外，c2dOptions 提供两个新选项

DelayModeling - 指定是将额外延迟建模为内部延迟（默认值）还是附加状态。
Consistency - 在状态空间数组中强制实现状态和延迟一致性。在离散化网格 LPV 或 LTV 模型时，此选项很有帮助。

另请参阅

c2d

语法

说明

示例

离散化传递函数

通过将小数延迟吸收到系数中来离散化模型

使用逼近的小数延迟离散化模型

离散化辨识的模型

构建预测器模型

输入参数

sysc — 连续时间动态系统 动态系统模型

Ts — 采样时间 正标量

method — 离散化方法 'zoh' (默认) | 'foh' | 'impulse' | 'tustin' | 'matched' | 'least-squares' | 'damped'

opts — 离散化选项 c2dOptions 对象

输出参量

sysd — 离散时间模型 动态系统模型

G — 状态空间模型的连续初始条件到离散时间初始状态向量的映射 矩阵

版本历史记录

R2024a: 在转换期间不添加额外状态

R2024a: 支持 mechss 模型

R2024a: 支持具有偏移量和其他改进的模型

另请参阅

主题

`sysc` — 连续时间动态系统
动态系统模型

`Ts` — 采样时间
正标量

`method` — 离散化方法
`'zoh'` (默认) | `'foh'` | `'impulse'` | `'tustin'` | `'matched'` | `'least-squares'` | `'damped'`

`opts` — 离散化选项
`c2dOptions` 对象

`sysd` — 离散时间模型
动态系统模型

`G` — 状态空间模型的连续初始条件到离散时间初始状态向量的映射
矩阵

R2024a: 支持 `mechss` 模型