tf

传递函数模型

全页展开

说明

使用 tf 创建实数值或复数值传递函数模型，或将动态系统模型转换为传递函数形式。

传递函数是线性时不变系统的频域表示。例如，假设有由传递函数 sys(s) = N(s)/D(s) 表示的连续时间 SISO 动态系统，其中 s = jw 且 N(s) 和 D(s) 分别称为分子和分母多项式。tf 模型对象可以表示连续时间或离散时间的 SISO 或 MIMO 传递函数。

您可以通过直接指定其系数或通过将另一种类型的模型（如状态空间模型 ss）转换为传递函数形式来创建传递函数模型对象。有关详细信息，请参阅传递函数。

您还可以使用 tf 来创建广义状态空间 (genss) 模型或不确定状态空间 (uss (Robust Control Toolbox)) 模型。

创建对象

语法

sys = tf(numerator,denominator)
sys = tf(numerator,denominator,ts)
sys = tf(numerator,denominator,ltiSys)
sys = tf(m)
sys = tf(___,PropertyName=Value)
sys = tf(ltiSys)
sys = tf(ltiSys,Name=Value)
sys = tf(ltiSys,component)
s = tf('s')
z = tf('z',ts)

描述

创建传递函数模型

sys = tf(numerator,denominator) 创建连续时间传递函数模型，设置 Numerator 和 Denominator 属性。例如，假设有由传递函数 sys(s) = N(s)/D(s) 表示的连续时间 SISO 动态系统，输入参量 numerator 和 denominator 分别是 N(s) 和 D(s) 的系数。

示例

sys = tf(numerator,denominator,ts) 创建离散时间传递函数模型，设置 Numerator、Denominator 和 Ts 属性。例如，假设有由传递函数 sys(z) = N(z)/D(z) 表示的离散时间 SISO 动态系统，输入参量 numerator 和 denominator 分别是 N(z) 和 D(z) 的系数。要保留采样时间为未指定状态，请将 ts 输入参量设置为 -1。

示例

sys = tf(numerator,denominator,ltiSys) 使用从动态系统模型 ltiSys 继承的属性（包括采样时间）创建一个传递函数模型。

示例

sys = tf(m) 创建一个表示静态增益 m 的传递函数模型。

示例

sys = tf(___,PropertyName=Value) 使用一个或多个属性名称-值参量为先前的任何输入参量组合设置传递函数模型的属性。

示例

转换为传递函数模型

sys = tf(ltiSys) 将动态系统模型 ltiSys 转换为传递函数模型。

示例

sys = tf(ltiSys,Name=Value) 通过基于一个或多个指定的名称-值参量计算零极点，获得稀疏模型 ltiSys 的截断传递函数表示。由于这种方法会为每个输入-输出对组计算零点，因此最适合输入-输出规模较小的模型。 (自 R2025a 起)

示例

sys = tf(ltiSys,component) 将 ltiSys 的指定 component 转换为传递函数形式。仅当 ltiSys 是辨识的线性时不变 (LTI) 模型时，才使用此语法。

示例

为有理式创建变量

s = tf('s') 创建特殊变量 s，您可以在有理式中使用该变量来创建连续时间传递函数模型。使用有理式有时比指定多项式系数更容易、更直观。

示例

z = tf('z',ts) 创建特殊变量 z，您可以在有理式中使用该变量来创建离散时间传递函数模型。要保留采样时间为未指定状态，请将 ts 输入参量设置为 -1。

示例

输入参量

全部展开

传递函数的分子系数，指定为：

  • 由多项式系数组成的行向量。

  • 由行向量组成的 Ny×Nu 元胞数组，用于指定 MIMO 传递函数，其中 Ny 是输出数目，Nu 是输入数目。

创建传递函数时，按降幂顺序指定分子系数。例如，如果传递函数的分子是 3s^2-4s+5，则将 numerator 指定为 [3 -4 5]。对于分子为 2z-1 的离散时间传递函数，将 numerator 设置为 [2 -1]。

它也是 tf 对象的一个属性。有关详细信息，请参阅 Numerator。

分母系数，指定为：

  • 由多项式系数组成的行向量。

  • 由行向量组成的 Ny×Nu 元胞数组，用于指定 MIMO 传递函数，其中 Ny 是输出数目，Nu 是输入数目。

创建传递函数时，按降幂顺序指定分母系数。例如，如果传递函数的分母是 7s^2+8s-9，则将 denominator 指定为 [7 8 -9]。对于分母为 2z^2+1 的离散时间传递函数，将 denominator 设置为 [2 0 1]。

它也是 tf 对象的一个属性。有关详细信息，请参阅 Denominator。

采样时间，指定为标量。它也是 tf 对象的一个属性。有关详细信息，请参阅 Ts。

动态系统，指定为 SISO 或 MIMO 动态系统模型或动态系统模型数组。您可以使用的动态系统包括：

  • 连续时间或离散时间数值 LTI 模型，如 tf、zpk、ss 或 pid 模型。

    如果 ltiSys 是稀疏状态空间模型（sparss 或 mechss），软件会通过在指定的关注频带内计算零极点，计算截断传递函数逼近。对于稀疏模型，请使用名称-值参量来指定计算选项。如果您不指定任何选项，软件最多可计算幅值最小的前 1000 个零极点。此外，获得此逼近仅适用于具有有效 sparss 表示的模型。 (自 R2025a 起)

  • 广义或不确定的 LTI 模型，如 genss 或 uss (Robust Control Toolbox) 模型。（使用不确定模型需要 Robust Control Toolbox™ 软件。）

    生成的传递函数假设

    • 对于可调控制设计模块，采用可调组件的当前值。

    • 对于不确定的控制设计模块，采用标称模型值。

  • 辨识的 LTI 模型，如 idtf (System Identification Toolbox)、idss (System Identification Toolbox)、idproc (System Identification Toolbox)、idpoly (System Identification Toolbox) 和 idgrey (System Identification Toolbox) 模型。要选择要转换的辨识模型的组件，请指定 component。如果未指定 component，则默认情况下，tf 会转换所辨识模型的被测组件。（使用辨识模型需要 System Identification Toolbox™ 软件。）

静态增益，指定为标量或矩阵。系统的静态增益或稳态增益表示在稳态条件下输出与输入的比率。

要转换的辨识模型的组件，指定为以下项之一：

  • 'measured' - 转换 sys 的被测组件。

  • 'noise' - 转换 sys 的噪声分量

  • 'augmented' - 转换 sys 的被测组件和噪声分量。

component 仅在 sys 是辨识的 LTI 模型时适用。

有关辨识的 LTI 模型及其被测组件和噪声分量的详细信息，请参阅Identified LTI Models。

名称-值参数

全部展开

以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

示例: sys = tf(sparseSys,Focus=[0 100],Display="off")

自 R2025a 起

在零极点计算期间使用并行计算，指定为数值或逻辑 0 (false) 或 1(true)。

当 UseParallel 设置为 true 时，您可以明确选择扩展到您的首选并行环境。启用并行计算可以提高零极点计算的性能。但是，即使 UseParallel 设置为 false，算法也可以使用内置的多线程来充分利用本地资源。有关详细信息，请参阅 MATLAB Multicore。

此选项需要 Parallel Computing Toolbox™ 许可证。

自 R2025a 起

滚降斜率，指定为非正标量或矩阵。

  • 对于 SISO 模型或者所有输入-输出对组的斜率相同的 MIMO 模型，使用标量值。

  • 对于每个输入-输出对组的斜率不同的 MIMO 模型，使用矩阵。

通过此选项，您可以显式指定在超出指定频率范围后，逼近应如何滚降。例如，Slope 为 -2 可确保增益在超过 fmax 后，以至少 -40 dB/十倍频程的速率（滚降率为 1/s2）滚降。

自 R2025a 起

关注的频率范围，指定为 [0,fmax] 形式的向量。当您指定关注的频率范围时，软件仅会计算固有频率在此范围内的极点。对于离散时间模型，软件通过突斯汀变换来逼近等效的固有频率。

由于 tf 会计算指定频率范围内的所有零极点，因此您通常会指定一个低频范围来限制计算大量零极点。默认情况下，不指定关注的频率范围 ([0 Inf])，并且算法最多计算 MaxNumber 个零极点。

自 R2025a 起

要计算的零极点的最大数目，指定为正整数。此值限制算法计算的零极点的数目，以及原始稀疏模型的逼近阶数。

自 R2025a 起

频谱偏移，指定为有限标量。

通过对 A-sigma*E 使用逆幂迭代法，软件会计算固有频率在指定范围 [0,fmax] 内的极点，从而获得最接近偏移量 sigma 的特征值。当 A 为奇异矩阵且 sigma 为零时，由于不存在逆矩阵，算法会失败。因此，对于具有积分作用的稀疏模型（s = 0，或对于离散时间模型，在 z = 1 时），您可以使用此选项将极点或零点隐式地偏移至最接近此偏移值的值。请指定一个不等于原始模型现有极点或零点值的偏移值。

自 R2025a 起

计算的零极点的精度容差，指定为正有限标量。此值控制逆幂迭代中计算得到的特征值的收敛。

自 R2025a 起

显示或隐藏进度报告，指定为 "off" 或 "on"。

输出参量

全部展开

输出系统模型，其返回值情况如下：

  • 当 numerator 和 denominator 输入参量是数值数组时，返回为传递函数 (tf) 模型。将 ltiSys 转换为 tf 模型类型时，sys 始终是 tf 模型对象。

  • 如果 numerator 或 denominator 输入参量包括可调参数，如 realp 参数或广义矩阵 (genmat)，则返回为广义状态空间模型 (genss) 对象。有关示例，请参阅可调低通滤波器。

  • 当 numerator 或 denominator 输入参量包括不确定参数时，返回为不确定状态空间模型 (uss) 对象。使用不确定模型需要 Robust Control Toolbox 软件。有关示例，请参阅Transfer Function with Uncertain Coefficients (Robust Control Toolbox)。

属性

全部展开

分子系数，指定为：

  • 由多项式系数组成的行向量，按降幂顺序排列（如果 Variable 值为 's'、'z'、'p' 或 'q'），或按升幂顺序排列（如果 Variable 值为 'z^-1' 或 'q^-1'）。

  • 由行向量组成的 Ny×Nu 元胞数组，用于指定 MIMO 传递函数，其中 Ny 是输出数目，Nu 是输入数目。元胞数组的每个元素指定给定输入/输出对组的分子系数。如果将 Numerator 和 Denominator 都指定为元胞数组，则它们必须具有相同的维度。

Numerator 的系数可以是实数值，也可以是复数值。

分母系数，指定为：

  • 由多项式系数组成的行向量，按降幂顺序排列（如果 Variable 值为 's'、'z'、'p' 或 'q'），或按升幂顺序排列（如果 Variable 值为 'z^-1' 或 'q^-1'）。

  • 由行向量组成的 Ny×Nu 元胞数组，用于指定 MIMO 传递函数，其中 Ny 是输出数目，Nu 是输入数目。元胞数组的每个元素指定给定输入/输出对组的分子系数。如果将 Numerator 和 Denominator 都指定为元胞数组，则它们必须具有相同的维度。

如果 MIMO 传递函数的所有 SISO 项都具有相同的分母，则可以将 Denominator 指定为行向量，将 Numerator 指定为元胞数组。

Denominator 的系数可以是实数值，也可以是复数值。

传递函数显示变量，指定为以下项之一：

  • 's' - 连续时间模型的默认值

  • 'z' - 离散时间模型的默认值

  • 'p' - 等效于 's'

  • 'q' - 等效于 'z'

  • 'z^-1' - 'z' 的倒数

  • 'q^-1' - 等效于 'z^-1'

Variable 的值反映在显示中，还会影响离散时间模型的 Numerator 和 Denominator 系数向量的解释。

  • 如果 Variable 值为 's'、'z'、'p' 或 'q'，系数将按变量的降幂顺序排列。例如，假设有行向量 [ak ... a1 a0]。多项式阶指定为 akzk+...+a1z+a0。

  • 如果 Variable 值为 'z^-1' 或 'q^-1'，系数将按变量的升幂顺序排列。例如，假设有行向量 [b0 b1 ... bk]。多项式阶指定为 b0+b1z−1+...+bkz−k。

有关示例，请参阅在离散时间传递函数中指定多项式排序、使用有理式的传递函数模型 和 使用有理式的离散时间传递函数模型。

传输延迟，指定为以下项之一：

  • 标量 - 为 SISO 系统指定传输延迟，或为 MIMO 系统的所有输入/输出对组指定相同的传输延迟。

  • Ny×Nu 数组 - 为 MIMO 系统的每个输入/输出对组指定单独的传输延迟。此处，Ny 是输出数目，Nu 是输入数目。

对于连续时间系统，以 TimeUnit 属性指定的时间单位指定传输延迟。对于离散时间系统，以采样时间 Ts 的整数倍指定传输延迟。

每个输入通道的输入延迟，指定为以下项之一：

  • 标量 - 为 SISO 系统指定输入延迟，或为多输入系统的所有输入指定相同的延迟。

  • Nu×1 向量 - 为多输入系统的输入指定单独的输入延迟，其中 Nu 是输入数。

对于连续时间系统，以 TimeUnit 属性指定的时间单位指定输入延迟。对于离散时间系统，以采样时间 Ts 的整数倍指定输入延迟。

有关详细信息，请参阅线性系统中的时滞。

每个输出通道的输出延迟，指定为以下项之一：

  • 标量 - 为 SISO 系统指定输出延迟，或为多输出系统的所有输出指定相同的延迟。

  • Ny×1 向量 - 为多输出系统的输出指定单独的输出延迟，其中 Ny 是输出数。

对于连续时间系统，以 TimeUnit 属性指定的时间单位指定输出延迟。对于离散时间系统，以采样时间 Ts 的整数倍指定输出延迟。

有关详细信息，请参阅线性系统中的时滞。

采样时间，指定为：

  • 0（适用于连续时间系统）。

  • 表示离散时间系统采样周期的正标量。以 TimeUnit 属性指定的时间单位指定 Ts。

  • -1（适用于未指定采样时间的离散时间系统）。

注意

更改 Ts 不会对模型进行离散化或重采样。要在连续时间和离散时间表示之间转换，请使用 c2d 和 d2c。要更改离散时间系统的采样时间，请使用 d2d。

时间变量单位，指定为以下项之一：

  • 'nanoseconds'

  • 'microseconds'

  • 'milliseconds'

  • 'seconds'

  • 'minutes'

  • 'hours'

  • 'days'

  • 'weeks'

  • 'months'

  • 'years'

更改 TimeUnit 不会影响其他属性，但会更改整体系统行为。可使用 chgTimeUnit 在不修改系统行为的情况下转换时间单位。

输入通道名称，指定为以下项之一：

  • 字符向量（适用于单输入模型）。

  • 字符向量元胞数组（适用于多输入模型）。

  • ''，不指定名称（适用于任何输入通道）。

您也可以使用自动向量扩展为多输入模型指定输入名称。例如，如果 sys 是双输入模型，请输入以下内容。

sys.InputName = 'controls';

输入名称会自动扩展为 {'controls(1)';'controls(2)'}。

您可以使用简化形式 u 来引用 InputName 属性。例如，sys.u 等效于 sys.InputName。

使用 InputName 可以：

  • 识别模型显示和绘图上的通道。

  • 提取 MIMO 系统的子系统。

  • 互连模型时指定连接点。

输入通道单位，指定为以下项之一：

  • 字符向量（适用于单输入模型）。

  • 字符向量元胞数组（适用于多输入模型）。

  • ''，不指定单位（适用于任何输入通道）。

使用 InputUnit 指定输入信号单位。InputUnit 不会影响系统行为。

输入通道组，指定为结构体。使用 InputGroup 将 MIMO 系统的输入通道分组，并按名称引用每个组。InputGroup 的字段名称是组名称，字段值是每个组的输入通道。例如，输入以下内容以创建名为 controls 和 noise 的输入组，它们分别包括输入通道 1 和 2 以及 3 和 5。

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

然后，您可以使用以下命令将子系统从 controls 输入提取到所有输出。

sys(:,'controls')

默认情况下，InputGroup 是不包含字段的结构体。

输出通道名称，指定为以下项之一：

  • 字符向量（适用于单输出模型）。

  • 字符向量元胞数组（适用于多输出模型）。

  • ''，不指定名称（适用于任何输出通道）。

您也可以使用自动向量扩展来为多输出模型指定输出名称。例如，如果 sys 是双输出模型，请输入以下内容。

sys.OutputName = 'measurements';

输出名称自动扩展为 {'measurements(1)';'measurements(2)'}。

您还可以使用简化形式 y 来引用 OutputName 属性。例如，sys.y 等效于 sys.OutputName。

使用 OutputName 可以：

  • 识别模型显示和绘图上的通道。

  • 提取 MIMO 系统的子系统。

  • 互连模型时指定连接点。

输出通道单位，指定为以下项之一：

  • 字符向量（适用于单输出模型）。

  • 字符向量元胞数组（适用于多输出模型）。

  • ''，不指定单位（适用于任何输出通道）。

使用 OutputUnit 指定输出信号单位。OutputUnit 不会影响系统行为。

输出通道组，指定为结构体。使用 OutputGroup 将 MIMO 系统的输出通道分组，并按名称引用每个组。OutputGroup 的字段名称是组名称，字段值是每个组的输出通道。例如，创建名为 temperature 和 measurement 的输出组，它们分别包括输出通道 1 以及 3 和 5。

sys.OutputGroup.temperature = [1];
sys.OutputGroup.measurement = [3 5];

然后，您可以使用以下命令将子系统从所有输入提取到 measurement 输出。

sys('measurement',:)

默认情况下，OutputGroup 是不包含字段的结构体。

系统名称，指定为字符向量。例如，'system_1'。

用户指定的要与系统关联的文本，指定为字符向量或字符向量元胞数组。例如，'System is MIMO'。

要与系统关联的用户指定数据，指定为任何 MATLAB 数据类型。

模型数组的采样网格，指定为结构体数组。

使用 SamplingGrid 跟踪与模型数组中每个模型相关联的变量值，包括辨识的线性时不变 (IDLTI) 模型数组。

将结构体的字段名称设置为采样变量的名称。将字段值设置为与数组中每个模型相关联的采样变量值。所有采样变量都必须为数值标量，所有由采样值组成的数组都必须与模型数组的维度匹配。

例如，您可以通过拍摄线性时变系统在时间 t = 0:10 处的快照，创建一个 11×1 线性模型数组 sysarr。以下代码随线性模型存储时间采样。

 sysarr.SamplingGrid = struct('time',0:10)

同样，您可以通过对两个变量 zeta 和 w 独立采样，创建一个 6×9 模型数组 M。以下代码将 (zeta,w) 值映射到 M。

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

当显示 M 时，数组中的每个条目都包括对应的 zeta 和 w 值。

M
M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

对于通过在多个参数值或工作点处线性化 Simulink® 模型生成的模型数组，软件会自动使用与数组中每个条目对应的变量值填充 SamplingGrid。例如，Simulink Control Design™ 命令 linearize (Simulink Control Design) 和 slLinearizer (Simulink Control Design) 会自动填充 SamplingGrid。

默认情况下，SamplingGrid 是不包含字段的结构体。

对象函数

以下列表包含可用于 tf 模型的部分代表性函数。一般情况下，任何适用于 动态系统模型 的函数也适用于 tf 对象。

全部展开

step动态系统的阶跃响应
impulse动态系统的冲激响应图；冲激响应数据
lsim计算动态系统对任意输入的时间响应仿真数据
bode动态系统的波特频率响应
nyquist动态系统的奈奎斯特响应
nichols动态系统的尼柯尔斯响应
bandwidth频率响应带宽
pole动态系统的极点
zeroSISO 动态系统的零点和增益
pzplotPlot pole-zero map of dynamic system
margin增益裕度、相位裕度和穿越频率
zpk零极点增益模型
ss状态空间模型
c2d将模型从连续时间转换为离散时间
d2c将模型从离散时间转换为连续时间
d2d重采样离散时间模型
feedback多个模型的反馈连接
connectBlock diagram interconnections of dynamic systems
series两个模型的串行连接
parallel两个模型的并行连接
pidtune线性被控对象模型的 PID 调节算法
rlocus动态系统的根轨迹
lqr线性二次调节器 (LQR) 设计
lqg线性二次高斯 (LQG) 设计
lqi线性二次积分控制
kalman设计用于状态估计的卡尔曼滤波器

示例

全部折叠

打开实时脚本

对于此示例，假设有以下 SISO 传递函数模型：

sys(s)=12s2+3s+4.

以 s 的降幂顺序指定分子和分母系数，并创建传递函数模型。

numerator = 1;
denominator = [2,3,4];
sys = tf(numerator,denominator)
sys =
 
         1
  ---------------
  2 s^2 + 3 s + 4
 
Continuous-time transfer function.
Model Properties
打开实时脚本

对于此示例，假设有以下离散时间 SISO 传递函数模型：

sys(z)=2z4z3+3z-1.

以 z 的降幂顺序指定分子和分母系数，并指定采样时间为 0.1 秒。创建离散时间传递函数模型。

numerator = [2,0];
denominator = [4,0,3,-1];
ts = 0.1;
sys = tf(numerator,denominator,ts)
sys =
 
        2 z
  ---------------
  4 z^3 + 3 z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties
打开实时脚本

对于此示例，假设有一个传递函数模型，它表示具有已知固有频率和阻尼比的二阶系统。

二阶系统的传递函数用其阻尼比 ζ 和固有频率 ω0 表示，如下所示：

sys(s)=ω02s2+2ζω0s+ω02.

假设阻尼比 ζ = 0.25，固有频率 ω0 = 3 弧度/秒，用它们来创建该二阶传递函数。

zeta = 0.25;
w0 = 3;
numerator = w0^2;
denominator = [1,2*zeta*w0,w0^2];
sys = tf(numerator,denominator)
sys =
 
         9
  ---------------
  s^2 + 1.5 s + 9
 
Continuous-time transfer function.
Model Properties

检查此传递函数对阶跃输入的响应。

stepplot(sys)

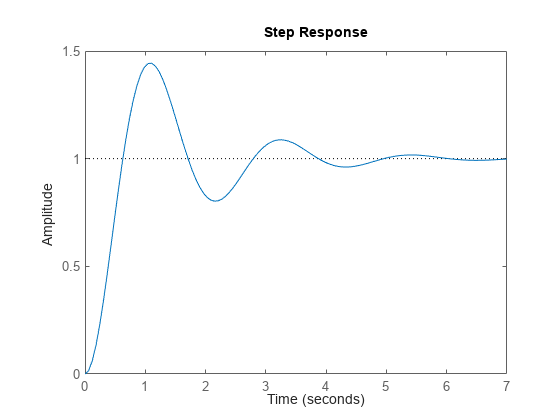
MATLAB figure

上图显示具有低阻尼比的二阶系统的预期衰荡。

打开实时脚本

创建离散时间多输入多输出模型的传递函数：

sys(z)=[1z+0.3zz+0.3-z+2z+0.33z+0.3]

采样时间为 ts = 0.2 秒。

将分子系数指定为 2×2 矩阵。

numerators = {1 [1 0];[-1 2] 3};

将公分母的系数指定为一个行向量。

denominator = [1 0.3];

创建离散时间 MIMO 传递函数模型。

ts = 0.2;
sys = tf(numerators,denominator,ts)
sys =
 
  From input 1 to output...
          1
   1:  -------
       z + 0.3
 
       -z + 2
   2:  -------
       z + 0.3
 
  From input 2 to output...
          z
   1:  -------
       z + 0.3
 
          3
   2:  -------
       z + 0.3
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

有关创建 MIMO 传递函数的详细信息，请参阅 MIMO 传递函数。

打开实时脚本

在此示例中，您需要通过串联 SISO 传递函数模型来创建一个 MIMO 传递函数模型。假设有以下单输入双输出传递函数：

sys(s)=[s-1s+1s+2s2+4s+5].

通过串联 SISO 条目来指定 MIMO 传递函数模型。

sys1 = tf([1 -1],[1 1]);		
sys2 = tf([1 2],[1 4 5]);
sys = [sys1;sys2]
sys =
 
  From input to output...
       s - 1
   1:  -----
       s + 1
 
           s + 2
   2:  -------------
       s^2 + 4 s + 5
 
Continuous-time transfer function.
Model Properties

有关创建 MIMO 传递函数的详细信息，请参阅 MIMO 传递函数。

打开实时脚本

对于此示例，请使用有理式创建一个连续时间传递函数模型。使用有理式有时比指定分子和分母的多项式系数更容易、更直观。

假设有以下系统：

sys(s)=ss2+2s+10.

要创建传递函数模型，请首先将 s 指定为 tf 对象。

s = tf('s')
s =
 
  s
 
Continuous-time transfer function.
Model Properties

在有理式中使用 s 创建传递函数模型。

sys = s/(s^2 + 2*s + 10)
sys =
 
        s
  --------------
  s^2 + 2 s + 10
 
Continuous-time transfer function.
Model Properties
打开实时脚本

对于此示例，请使用有理式创建一个离散时间传递函数模型。使用有理式有时比指定多项式系数更容易、更直观。

假设有以下系统：

sys(z)=z-1z2-1.85z+0.9.Discrete-time transfer function

要创建传递函数模型，请首先将 z 指定为 tf 对象，并将采样时间指定为 Ts。

ts = 0.1;
z = tf('z',ts)
z =
 
  z
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

在有理式中使用 z 创建传递函数模型。

sys = (z - 1) / (z^2 - 1.85*z + 0.9)
sys =
 
        z - 1
  ------------------
  z^2 - 1.85 z + 0.9
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties
打开实时脚本

对于此示例，请使用从另一个传递函数模型继承的属性创建一个传递函数模型。假设有以下两个传递函数：

sys1(s)=2ss2+8sandsys2(s)=s-17s4+2s3+9.

对于此示例，请创建 sys1 并将 TimeUnit 和 InputDelay 属性设置为 'minutes'。

numerator1 = [2,0];
denominator1 = [1,8,0];
sys1 = tf(numerator1,denominator1,'TimeUnit','minutes','InputUnit','minutes')
sys1 =
 
     2 s
  ---------
  s^2 + 8 s
 
Continuous-time transfer function.
Model Properties

propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1×2 cell
    {'minutes'}    {'minutes'}

使用从 sys1 继承的属性创建第二个传递函数模型。

numerator2 = [1,-1];
denominator2 = [7,2,0,0,9];
sys2 = tf(numerator2,denominator2,sys1)
sys2 =
 
        s - 1
  -----------------
  7 s^4 + 2 s^3 + 9
 
Continuous-time transfer function.
Model Properties

propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1×2 cell
    {'minutes'}    {'minutes'}

注意观察，传递函数模型 sys2 具有与 sys1 相同的属性。

打开实时脚本

您可以使用 for 循环来指定一个传递函数模型数组。

首先，为传递函数数组预分配零值。

sys = tf(zeros(1,1,3));

前两个索引表示模型的输出和输入数目，而第三个索引是数组中模型的数目。

在 for 循环中使用有理式创建传递函数模型数组。

s = tf('s');                                                  
for k = 1:3                                                             
    sys(:,:,k) = k/(s^2+s+k);                                          
end
sys
sys(:,:,1,1) =
 
       1
  -----------
  s^2 + s + 1
 

sys(:,:,2,1) =
 
       2
  -----------
  s^2 + s + 2
 

sys(:,:,3,1) =
 
       3
  -----------
  s^2 + s + 3
 
3x1 array of continuous-time transfer functions.
Model Properties
打开实时脚本

对于此示例，计算以下状态空间模型的传递函数：

A=[-2-11-2],B=[112-1],C=[10],D=[01].

使用状态空间矩阵创建状态空间模型。

A = [-2 -1;1 -2];
B = [1 1;2 -1];
C = [1 0];
D = [0 1];
ltiSys = ss(A,B,C,D);

将状态空间模型 ltiSys 转换为传递函数。

sys = tf(ltiSys)
sys =
 
  From input 1 to output:
        s
  -------------
  s^2 + 4 s + 5
 
  From input 2 to output:
  s^2 + 5 s + 8
  -------------
  s^2 + 4 s + 5
 
Continuous-time transfer function.
Model Properties

此示例使用:

打开实时脚本

对于此示例，将辨识的多项式模型的被测组件和噪声分量提取为两个单独的传递函数。

在 identifiedModel.mat 中加载博克斯-詹金斯多项式模型 ltiSys。

load('identifiedModel.mat','ltiSys');

ltiSys 是辨识的离散时间模型，其形式为：y(t)=BFu(t)+CDe(t)，其中 BF 表示被测组件，CD 表示噪声分量。

将被测组件和噪声分量提取为传递函数。 

sysMeas = tf(ltiSys,'measured') 
sysMeas =
 
  From input "u1" to output "y1":
            -0.1426 z^-1 + 0.1958 z^-2
  z^(-2) * ----------------------------
           1 - 1.575 z^-1 + 0.6115 z^-2
 
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties

sysNoise = tf(ltiSys,'noise')
sysNoise =
 
  From input "v@y1" to output "y1":
           0.04556 + 0.03301 z^-1
  ----------------------------------------
  1 - 1.026 z^-1 + 0.26 z^-2 - 0.1949 z^-3
 
Input groups:        
    Name     Channels
    Noise       1    
                     
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties

被测组件可以用作被控对象模型，而噪声分量可以用作控制系统设计的扰动模型。

打开实时脚本

传递函数模型对象包括模型数据，这些数据有助于您跟踪模型所表示的内容。例如，您可以为模型的输入和输出指定名称。

假设有以下连续时间 MIMO 传递函数模型：

sys(s)=[s+1s2+2s+21s]

该模型有一个输入 - 电流，有两个输出 - 扭矩和角速度。

首先，指定模型的分子和分母系数。

numerators = {[1 1] ; 1};
denominators = {[1 2 2] ; [1 0]};

创建传递函数模型，指定输入名称和输出名称。

sys = tf(numerators,denominators,'InputName','Current',...
        'OutputName',{'Torque' 'Angular Velocity'})
sys =
 
  From input "Current" to output...
                s + 1
   Torque:  -------------
            s^2 + 2 s + 2
 
                      1
   Angular Velocity:  -
                      s
 
Continuous-time transfer function.
Model Properties
打开实时脚本

对于此示例，请使用 'Variable' 属性指定离散时间传递函数模型中的多项式排序。

假设有以下离散时间传递函数，其采样时间为 0.1 秒：

sys1(z)=z2z2+2z+3sys2(z-1)=11+2z-1+3z-2.

通过指定 z 系数，创建第一个离散时间传递函数。 

numerator = [1,0,0];
denominator = [1,2,3];
ts = 0.1;
sys1 = tf(numerator,denominator,ts)
sys1 =
 
       z^2
  -------------
  z^2 + 2 z + 3
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

sys1 的系数按 z 的降幂顺序排列。

tf 根据 'Variable' 属性的值切换约定。由于 sys2 是 sys1 的逆传递函数模型，因此请将 'Variable' 指定为 'z^-1' 并使用相同的分子和分母系数。 

sys2 = tf(numerator,denominator,ts,'Variable','z^-1')
sys2 =
 
           1
  -------------------
  1 + 2 z^-1 + 3 z^-2
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

sys2 的系数现在以 z^-1 的升幂顺序排列。

根据不同约定，您可以使用 'Variable' 属性在传递函数模型中指定多项式排序。

打开实时脚本

在此示例中，您将创建具有一个可调参数 a 的低通滤波器：

F=as+a

由于 tunableTF 模块的分子和分母系数是独立的，您无法用 tunableTF 来表示 F。在这种情况下，您可以使用可调实数参数对象 realp 来构造 F。

创建一个初始值为 10 的实数可调参数。

a = realp('a',10)
a = 
       Name: 'a'
      Value: 10
    Minimum: -Inf
    Maximum: Inf
       Free: 1

Real scalar parameter.

使用 tf 创建可调低通滤波器 F。

numerator = a;
denominator = [1,a];
F = tf(numerator,denominator)
Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks:
  a: Scalar parameter, 2 occurrences.
Model Properties

Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.

F 是一个 genss 对象，在其 Blocks 属性中具有可调参数 a。您可以将 F 与其他可调模型或数值模型连接，以创建更复杂的控制系统模型。有关示例，请参阅Control System with Tunable Components。

打开实时脚本

此示例中，您将创建一个静态增益 MIMO 传递函数模型。

假设有以下双输入双输出静态增益矩阵 m：

m=[2435]

指定增益矩阵并创建静态增益传递函数模型。 

m = [2,4;...
    3,5];
sys1 = tf(m)
sys1 =
 
  From input 1 to output...
   1:  2
 
   2:  3
 
  From input 2 to output...
   1:  4
 
   2:  5
 
Static gain.
Model Properties

您可以使用上面获得的静态增益传递函数模型 sys1 将其与另一个传递函数模型级联。

对于此示例，创建另一个双输入双输出离散传递函数模型，并使用 series 函数连接这两个模型。 

numerators = {1,[1,0];[-1,2],3};
denominator = [1,0.3];
ts = 0.2;
sys2 = tf(numerators,denominator,ts)
sys2 =
 
  From input 1 to output...
          1
   1:  -------
       z + 0.3
 
       -z + 2
   2:  -------
       z + 0.3
 
  From input 2 to output...
          z
   1:  -------
       z + 0.3
 
          3
   2:  -------
       z + 0.3
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

sys = series(sys1,sys2)
sys =
 
  From input 1 to output...
       3 z^2 + 2.9 z + 0.6
   1:  -------------------
       z^2 + 0.6 z + 0.09
 
       -2 z^2 + 12.4 z + 3.9
   2:  ---------------------
        z^2 + 0.6 z + 0.09
 
  From input 2 to output...
       5 z^2 + 5.5 z + 1.2
   1:  -------------------
       z^2 + 0.6 z + 0.09
 
       -4 z^2 + 21.8 z + 6.9
   2:  ---------------------
        z^2 + 0.6 z + 0.09
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

自 R2025a 起

打开实时脚本

此示例说明如何获得稀疏状态空间模型的截断传递函数模型。此示例使用了一个通过对圆柱杆中热分布的热模型进行线性化得到的稀疏模型。

加载模型数据。

load cylindricalRod.mat
sys = sparss(A,B,C,D,E);
w = logspace(-7,-1,20);
size(sys)
Sparse state-space model with 3 outputs, 1 inputs, and 7522 states.

分析该模型的频率响应。

sigmaplot(sys,w)

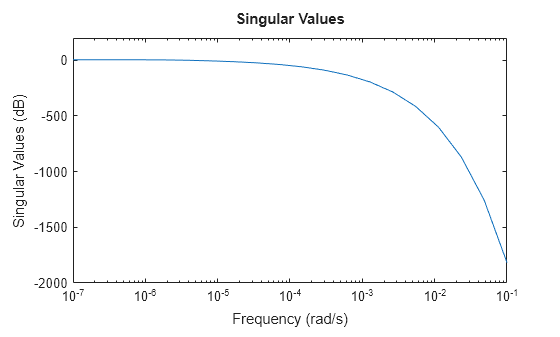
MATLAB figure

为了获得截断逼近，请使用 tf 并指定关注的频带。对于此模型，您可以使用 0 弧度/秒到 0.01 弧度/秒的频率范围来获得低阶逼近。

tsys = tf(sys,Focus=[0 1e-2],Display="off");

比较频率响应。

sigmaplot(sys,tsys,w)

MATLAB figure

此热模型在超过 0.001 弧度/秒后具有非常陡峭的滚降。默认情况下，使用 tf 获得的降阶模型在此滚降特性上无法很好地匹配。为了解决这个问题，您可以使用 tf 的 RollOff 参量，并指定超过关注的频带后的最小滚降值。请指定滚降斜率值为 -45，该值对应于至少 –900 db/十倍频程的速率。

tsys2 = tf(sys,Focus=[0 1e-2],RollOff=-45,Display="off");
sigmaplot(sys,tsys2,w)

MATLAB figure

现在，降阶模型对滚降值的逼近效果要好得多。然而，在此示例中，使用 tf 重新调整滚降斜率需要重新计算零极点。对于大型模型来说，这意味着计算成本可能相当高。作为替代方案，您可以在软件计算零极点完毕后，使用 reducespec 的零极点截断方法并调整滚降，而无需额外的计算成本。有关示例，请参阅Zero-Pole Truncation of Thermal Model。

限制

  • 传递函数模型不适合数值计算。创建传递函数模型后，在将它们与其他模型结合或执行模型变换之前，请将它们变换为状态空间形式。然后，您可以将生成的模型转换回传递函数形式以进行检查。

  • 使用 tf 无法将辨识的非线性模型直接转换为传递函数模型。要获得传递函数模型，请执行下列步骤：

    1. 使用 linapp (System Identification Toolbox)、idnlarx/linearize (System Identification Toolbox) 或 idnlhw/linearize (System Identification Toolbox) 将非线性辨识模型转换为辨识的 LTI 模型。

    2. 然后，使用 tf 将生成的模型转换为传递函数模型。

算法

为了转换稀疏模型，tf 使用 Krylov--Schur 算法 [1] 进行逆幂迭代，以计算指定频率带内的零极点。

参考

[1] Stewart, G. W. “A Krylov--Schur Algorithm for Large Eigenproblems.” SIAM Journal on Matrix Analysis and Applications 23, no. 3 (January 2002): 601–14. https://doi.org/10.1137/S0895479800371529.

版本历史记录

在 R2006a 之前推出

全部展开

另请参阅

| | | | | | | | | |

主题

外部网站