lqi

线性二次积分控制

语法

[K,S,e] = lqi(SYS,Q,R,N)

说明

lqi 为下图所示的跟踪环计算最优状态反馈控制律。

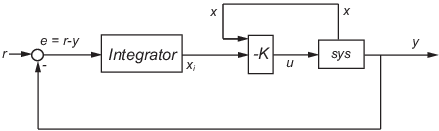
对于具有状态空间方程（或其离散对应方程）的被控对象 sys：

$\begin{array}{l} \frac{d x}{d t} = A x + B u \\ y = C x + D u \end{array}$

状态反馈控制的形式为

$u = - K [x; x_{i}]$

其中 x_i 是积分器输出。此控制律确保输出 y 跟踪参考命令 r。对于 MIMO 系统，积分器的数量等于输出 y 的维度。

[K,S,e] = lqi(SYS,Q,R,N) 基于给定的被控对象状态空间模型 SYS 和加权矩阵 Q、R 和 N，计算最优增益矩阵 K。控制律 u = –Kz = –K[x;x_i] 最小化以下代价函数（对于 r = 0）

$J (u) = \int_{0}^{\infty} {z^{T} Q z + u^{T} R u + 2 z^{T} N u} d t$ （适用于连续时间）
$J (u) = \sum_{n = 0}^{\infty} {z^{T} Q z + u^{T} R u + 2 z^{T} N u}$ （适用于离散时间）

在离散时间中，lqi 使用前向欧拉公式

$x_{i} [n + 1] = x_{i} [n] + T s (r [n] - y [n])$

计算积分器输出 x_i，其中 Ts 是 SYS 的采样时间。

当您省略矩阵 N 时，N 设置为 0。lqi 还返回相关联的代数黎卡提方程的解 S 和闭环特征值 e。

限制

对于以下带增强积分器的被控对象的状态空间系统：

$\begin{array}{l} \frac{δ z}{δ t} = A_{a} z + B_{a} u \\ y = C_{a} z + D_{a} u \end{array}$

问题数据必须满足：

对组 (A,B) 必须是可稳定的。
R 必须为正定矩阵。
$[\begin{matrix} Q & N \\ N^{T} & R \end{matrix}]$ 必须为半正定矩阵（等效于 $Q - N R^{- 1} N^{T} \geq 0$ ）。
$(Q - N R^{- 1} N^{T}, A_{a} - B_{a} R^{- 1} N^{T})$ 在虚轴（或离散时间的单位圆）上必须没有无法观测的模态。

提示

lqi 支持描述符形式的模型，其中包含非奇异矩阵 E。lqi 的输出 S 是以下等效显式状态空间模型的黎卡提方程的解：

$\frac{d x}{d t} = E^{- 1} A x + E^{- 1} B u$

参考资料

[1] P. C. Young and J. C. Willems, "An approach to the linear multivariable servomechanism problem", International Journal of Control, Volume 15, Issue 5, May 1972 , pages 961–979.

版本历史记录

在 R2008b 中推出

另请参阅